The HPQUANTSELECT Procedure
Getting Started: HPQUANTSELECT Procedure
The following example is modeled on the example in the section "Getting Started: QUANTSELECT Procedure" in the
SAS/STAT User's Guide. The Sashelp.baseball data set contains salary and performance information for Major League Baseball (MLB) players, excluding pitchers, who played
in at least one game in both the 1986 and 1987 seasons. The salaries (Time Inc. 1987) are for the 1987 season, and the performance measures are for the 1986 season (Reichler 1987).
The following statements display the variables in the data set. Figure 14.2 shows the results.
proc contents varnum data=sashelp.baseball; ods select position; run;
Figure 14.2: Sashelp.Baseball Data Set
| Variables in Creation Order | ||||
|---|---|---|---|---|
| # | Variable | Type | Len | Label |
| 1 | Name | Char | 18 | Player's Name |
| 2 | Team | Char | 14 | Team at the End of 1986 |
| 3 | nAtBat | Num | 8 | Times at Bat in 1986 |
| 4 | nHits | Num | 8 | Hits in 1986 |
| 5 | nHome | Num | 8 | Home Runs in 1986 |
| 6 | nRuns | Num | 8 | Runs in 1986 |
| 7 | nRBI | Num | 8 | RBIs in 1986 |
| 8 | nBB | Num | 8 | Walks in 1986 |
| 9 | YrMajor | Num | 8 | Years in the Major Leagues |
| 10 | CrAtBat | Num | 8 | Career Times at Bat |
| 11 | CrHits | Num | 8 | Career Hits |
| 12 | CrHome | Num | 8 | Career Home Runs |
| 13 | CrRuns | Num | 8 | Career Runs |
| 14 | CrRbi | Num | 8 | Career RBIs |
| 15 | CrBB | Num | 8 | Career Walks |
| 16 | League | Char | 8 | League at the End of 1986 |
| 17 | Division | Char | 8 | Division at the End of 1986 |
| 18 | Position | Char | 8 | Position(s) in 1986 |
| 19 | nOuts | Num | 8 | Put Outs in 1986 |
| 20 | nAssts | Num | 8 | Assists in 1986 |
| 21 | nError | Num | 8 | Errors in 1986 |
| 22 | Salary | Num | 8 | 1987 Salary in $ Thousands |
| 23 | Div | Char | 16 | League and Division |
| 24 | logSalary | Num | 8 | Log Salary |
Suppose you want to investigate how the MLB players’ salaries for the 1987 season depend on performance measures for the players’ previous season and MLB career. You might worry that some players who are outliers could dominate your least squares analysis. To address this concern, you can use the following statements to obtain a median regression model, which is equivalent to the 50th conditional percentile or the quantile regression model at quantile level 0.5:
proc hpquantselect data=sashelp.baseball;
class league division;
model Salary = nAtBat nHits nHome nRuns nRBI nBB
yrMajor crAtBat crHits crHome crRuns crRbi
crBB league division nOuts nAssts nError
/ clb;
run;
The CLB option in the MODEL statement requests 95% confidence limits for the parameter estimates. If you do not use the SELECTION statement, the HPQUANTSELECT procedure fits the full model that is specified by the MODEL statement without any effect selection.
Figure 14.3: Performance, Data Access, and Model Information
Figure 14.3 displays the "Performance Information," "Data Access Information," and "Model Information" tables.
The "Performance Information" table shows that the HPQUANTSELECT procedure executes in client mode—that is, the model is fit on the machine where the SAS session executes. This step was performed on a multicore machine that contained four CPUs; one computational thread was spawned per CPU.
The "Data Access Information" table shows that the input data set is accessed with the V9 (base) engine on the client machine.
The "Model Information" table identifies the data source and response and shows that the CLASS variables are parameterized in the GLM parameterization, which is the default.
Figure 14.4: Number of Observations, Class Level Information, and Dimensions Tables
Figure 14.4 displays the "Number of Observations," "Class Level Information," and "Dimensions" tables.
The "Number of Observations" table shows that, of the 322 observations, PROC HPQUANTSELECT uses only 263 observations for model fitting and ignores 59 incomplete observations.
The "Class Level Information" table shows level information for two CLASS effects that the CLASS
statement identifies: League and Division. League has two levels: American League and National League. Division also has two levels: East Division and West Division.
The "Dimensions" table shows that the MODEL statement identifies 19 effects for model fitting besides the intercept effect. Because the 19 effects include two CLASS effects and each level of a CLASS effect corresponds to a parameter, the 19 effects contain a total of 21 parameters.
Figure 14.5: Fit Statistics
Figure 14.5 displays the "Fit Statistics" table, which shows the values of model fitting criteria for the fitted median model. For more
information about model fitting criteria for quantile regression, see the section Details: HPQUANTSELECT Procedure.
Figure 14.6: Parameter Estimates
| Parameter Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
95% Confidence Limits | t Value | Pr > |t| | |
| Intercept | 1 | -67.75322 | 39.95908 | -146.46197 | 10.95553 | -1.70 | 0.0912 |
| nAtBat | 1 | -1.57112 | 0.44700 | -2.45160 | -0.69064 | -3.51 | 0.0005 |
| nHits | 1 | 8.82192 | 1.94990 | 4.98114 | 12.66270 | 4.52 | <.0001 |
| nHome | 1 | -5.91757 | 4.91015 | -15.58926 | 3.75412 | -1.21 | 0.2293 |
| nRuns | 1 | -5.17076 | 2.14914 | -9.40400 | -0.93753 | -2.41 | 0.0169 |
| nRBI | 1 | 0.77547 | 2.15469 | -3.46870 | 5.01963 | 0.36 | 0.7192 |
| nBB | 1 | 5.28866 | 1.67603 | 1.98732 | 8.59000 | 3.16 | 0.0018 |
| YrMajor | 1 | 6.61877 | 6.61798 | -6.41690 | 19.65444 | 1.00 | 0.3182 |
| CrAtBat | 1 | -0.04463 | 0.15485 | -0.34964 | 0.26038 | -0.29 | 0.7734 |
| CrHits | 1 | 0.07896 | 0.73594 | -1.37064 | 1.52857 | 0.11 | 0.9146 |
| CrHome | 1 | 3.78231 | 1.90065 | 0.03854 | 7.52607 | 1.99 | 0.0477 |
| CrRuns | 1 | 1.23105 | 0.77137 | -0.28833 | 2.75044 | 1.60 | 0.1118 |
| CrRbi | 1 | -0.70695 | 0.76888 | -2.22144 | 0.80754 | -0.92 | 0.3588 |
| CrBB | 1 | -0.68911 | 0.41382 | -1.50423 | 0.12601 | -1.67 | 0.0971 |
| League American | 1 | -34.39136 | 24.37175 | -82.39724 | 13.61451 | -1.41 | 0.1595 |
| League National | 0 | 0 | . | . | . | . | . |
| Division East | 1 | 60.30856 | 27.28730 | 6.55984 | 114.05728 | 2.21 | 0.0280 |
| Division West | 0 | 0 | . | . | . | . | . |
| nOuts | 1 | 0.23273 | 0.12110 | -0.00581 | 0.47126 | 1.92 | 0.0558 |
| nAssts | 1 | 0.09824 | 0.18888 | -0.27381 | 0.47029 | 0.52 | 0.6035 |
| nError | 1 | -0.81574 | 3.51436 | -7.73810 | 6.10661 | -0.23 | 0.8166 |
Figure 14.6 displays the "Parameter Estimates" table, which shows the parameter estimates of the fitted median model. You can see that,
of the 19 effective parameters whose degrees of freedom are not zero, the fitted model contains 13 insignificant parameters
whose 95% confidence intervals cover zeros. Because more than half of the 19 effective parameters are insignificant, you might
worry that the model is overfitted.
It is well known that both overfitting and underfitting harm the prediction performance of a model. You can prevent overfitting
and underfitting by using a good effect-selection technique. The following statements apply the forward selection method and
the SL (significance level) criterion to choose a parsimonious model for the Sashelp.baseball data set:
proc hpquantselect data=sashelp.baseball;
class league division;
model Salary = nAtBat nHits nHome nRuns nRBI nBB
yrMajor crAtBat crHits crHome crRuns crRbi
crBB league division nOuts nAssts nError
/ clb;
selection method=forward(select=sl sle=0.1);
run;
The SLE=0.1 option in the SELECTION statement specifies the significance level for entry. A candidate effect can enter the model at a certain selection step only if the following conditions are met:
-
Its p-value is the smallest among all the valid candidate effects.
-
Its p-value is smaller than 0.1 (the significance level for entry).
For more information about using significance levels in effect selection, see the section Statistical Tests for Significance Level.
Figure 14.7: Selection Information
Figure 14.7 displays the "Selection Information" table. The "Selection Information" provides details about the method and criteria used
to perform the model selection. The requested selection method is the forward selection method where the decisions about what
effects to add at any step and when to terminate the selection are both based on the significance level criterion.
Figure 14.8: Selection Summary
Figure 14.8 displays the "Selection Summary" table. Each row in the "Selection Summary" table shows the effect that enters the model
at the corresponding step of the effect selection process together with its p-value for adding the effect into the model at that step.
Figure 14.9: Stopping and Selection Reasons
Figure 14.9 displays the "Stop Reason," "Selection Reason," and "Selected Effects" tables. The "Stop Reason" and "Selection Reason" tables
indicate that effect selection stopped because no candidate for entry was significant at the 0.1 level after step 8. The "Selected
Effects" table lists the effects that are included in the selected model.
Figure 14.10: Details of the Selected Model
| Parameter Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
95% Confidence Limits | t Value | Pr > |t| | |
| Intercept | 1 | -130.65536 | 33.04546 | -195.73336 | -65.57735 | -3.95 | <.0001 |
| nAtBat | 1 | -1.20522 | 0.41690 | -2.02624 | -0.38419 | -2.89 | 0.0042 |
| nHits | 1 | 7.76667 | 1.81045 | 4.20127 | 11.33207 | 4.29 | <.0001 |
| nRuns | 1 | -3.92180 | 1.87567 | -7.61566 | -0.22795 | -2.09 | 0.0375 |
| nBB | 1 | 3.92049 | 1.04341 | 1.86565 | 5.97532 | 3.76 | 0.0002 |
| CrHits | 1 | 0.17697 | 0.06856 | 0.04195 | 0.31198 | 2.58 | 0.0104 |
| CrHome | 1 | 1.66939 | 0.73083 | 0.23012 | 3.10866 | 2.28 | 0.0232 |
| Division East | 1 | 65.14327 | 24.48038 | 16.93289 | 113.35364 | 2.66 | 0.0083 |
| Division West | 0 | 0 | . | . | . | . | . |
| nOuts | 1 | 0.23719 | 0.11403 | 0.01261 | 0.46176 | 2.08 | 0.0385 |
The "Fit Statistics" and "Parameter Estimates" tables in Figure 14.10 give details of the final selected model. You can see that all nine effective parameters (excluding Division West) are significant
at the 5% significance level, corresponding to the 95% confidence limits.
Like the sample median, a median regression model is robust to extreme observations, because it depends only on a small middle
subset of all the observations in the data set. However, it is less representative of the entire conditional distribution
of the response variable. You might want to further investigate the Sashelp.baseball data set at other quantile levels. The following statements select quantile regression models at the quantile levels 0.1
and 0.9, which correspond to the 10% and 90% conditional percentiles of the players’ salaries:
proc hpquantselect data=sashelp.baseball alpha=0.1;
class league division;
model Salary = nAtBat nHits nHome nRuns nRBI nBB
yrMajor crAtBat crHits crHome crRuns crRbi
crBB league division nOuts nAssts nError
/ quantile=0.1 0.9 clb;
selection method=backward(select=sl sls=0.1);
run;
The ALPHA=0.1 option in the PROC statement sets the significance level to 0.1. Combined with the CLB option in the MODEL statement, the ALPHA=0.1 option requests 90% confidence limits for parameter estimates. The QUANTILE= option in the MODEL statement specifies two quantile levels, 0.1 and 0.9, for fitting quantile regression models. The METHOD=BACKWARD option in the SELECTION statement specifies the backward elimination method of effect selection.
Figure 14.11: Parameter Estimates at Quantile Level 0.1
| Parameter Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
90% Confidence Limits | t Value | Pr > |t| | |
| Intercept | 1 | 4.75224 | 18.94983 | -26.53111 | 36.03558 | 0.25 | 0.8022 |
| nAtBat | 1 | -0.73670 | 0.17958 | -1.03316 | -0.44024 | -4.10 | <.0001 |
| nHits | 1 | 2.69396 | 0.63510 | 1.64551 | 3.74241 | 4.24 | <.0001 |
| nBB | 1 | 1.81807 | 0.40595 | 1.14791 | 2.48823 | 4.48 | <.0001 |
| CrRuns | 1 | 0.65476 | 0.09560 | 0.49694 | 0.81259 | 6.85 | <.0001 |
| CrBB | 1 | -0.44622 | 0.16254 | -0.71454 | -0.17790 | -2.75 | 0.0065 |
| Division East | 1 | 28.35406 | 10.68922 | 10.70774 | 46.00038 | 2.65 | 0.0085 |
| Division West | 0 | 0 | . | . | . | . | . |
| nAssts | 1 | 0.14958 | 0.05897 | 0.05223 | 0.24694 | 2.54 | 0.0118 |
Figure 14.11 displays the "Selected Effects" and "Parameter Estimates" tables at quantile level 0.1.
Figure 14.12: Parameter Estimates at Quantile Level 0.9
| Parameter Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
90% Confidence Limits | t Value | Pr > |t| | |
| Intercept | 1 | 20.39804 | 58.17164 | -75.63745 | 116.43353 | 0.35 | 0.7261 |
| nHits | 1 | 2.30897 | 0.55640 | 1.39042 | 3.22752 | 4.15 | <.0001 |
| nBB | 1 | 3.09799 | 1.44414 | 0.71386 | 5.48213 | 2.15 | 0.0329 |
| CrAtBat | 1 | -0.44914 | 0.14651 | -0.69101 | -0.20727 | -3.07 | 0.0024 |
| CrHits | 1 | 2.48064 | 0.51725 | 1.62672 | 3.33457 | 4.80 | <.0001 |
| CrHome | 1 | 6.29896 | 1.37134 | 4.03502 | 8.56291 | 4.59 | <.0001 |
| CrRbi | 1 | -2.12293 | 0.76546 | -3.38662 | -0.85923 | -2.77 | 0.0060 |
| League American | 1 | -103.28955 | 33.68480 | -158.89975 | -47.67935 | -3.07 | 0.0024 |
| League National | 0 | 0 | . | . | . | . | . |
| Division East | 1 | 107.46694 | 50.82797 | 23.55512 | 191.37876 | 2.11 | 0.0355 |
| Division West | 0 | 0 | . | . | . | . | . |
| nOuts | 1 | 0.39766 | 0.12820 | 0.18601 | 0.60931 | 3.10 | 0.0021 |
Figure 14.11 displays the "Selected Effects" and "Parameter Estimates" tables at quantile level 0.9.
You might want to compute the 90th percentile predictions for players’ salaries and find out which players were overpaid based
on the quantile regression model at quantile level 0.9. The following statements repeat the backward elimination method at
quantile level 0.9, compute and sort the overpaid players’ salaries, and output the observations for the top 10 overpaid players
in the Sashelp.baseball data set:
proc hpquantselect data=sashelp.baseball alpha=0.1;
id Name;
class league division;
model Salary = nAtBat nHits nHome nRuns nRBI nBB
yrMajor crAtBat crHits crHome crRuns crRbi
crBB league division nOuts nAssts nError
/ quantile=0.9 clb;
selection method=backward(select=sl sls=0.1);
output out=BaseballOverpaid copyvar=Salary r=Overpaid
p=PredictedSalary lclm uclm;
run;
proc sort data=BaseballOverpaid;
by descending Overpaid;
run;
proc print data=BaseballOverpaid(obs=10);
var Name Salary Overpaid PredictedSalary lclm uclm;
run;
The ID
statement adds the variable Name from the input data set to the BaseballOverpaid data set that is produced by the OUTPUT
statement. The LCLM and UCLM options, respectively, request lower and upper bounds of 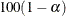 % confidence intervals for the expected conditional quantile predictions of players’ salaries at quantile level 0.9.
% confidence intervals for the expected conditional quantile predictions of players’ salaries at quantile level 0.9.
Figure 14.13: Top 10 Overpaid Baseball Players at Quantile Level 0.9
| Obs | Name | Salary | Overpaid | PredictedSalary | LCLM | UCLM |
|---|---|---|---|---|---|---|
| 1 | Smith, Ozzie | 1940.0 | 1084.54 | 855.46 | 611.09 | 1099.83 |
| 2 | Wiggins, Alan | 700.0 | 220.74 | 479.26 | 345.93 | 612.60 |
| 3 | Murray, Eddie | 2460.0 | 213.10 | 2246.90 | 1982.06 | 2511.74 |
| 4 | Strawberry, Darryl | 1220.0 | 187.64 | 1032.36 | 914.99 | 1149.72 |
| 5 | Gibson, Kirk | 1300.0 | 177.24 | 1122.76 | 1011.97 | 1233.56 |
| 6 | Trevino, Alex | 512.5 | 149.70 | 362.80 | 273.17 | 452.43 |
| 7 | Ramirez, Rafael | 875.0 | 141.09 | 733.91 | 599.52 | 868.31 |
| 8 | Romero, Ed | 375.0 | 128.71 | 246.29 | 144.88 | 347.70 |
| 9 | Mattingly, Don | 1975.0 | 124.82 | 1850.18 | 1557.81 | 2142.55 |
| 10 | Puhl, Terry | 900.0 | 104.34 | 795.66 | 625.51 | 965.81 |
Figure 14.13 shows the information about the top 10 overpaid players according to the final selected quantile regression model at quantile
level 0.9. Ozzie Smith is in first place. This might be because, although Smith was known for his defensive brilliance, the
model weights offensive performance measures much more than defensive performance measures.
