The HPQUANTSELECT Procedure

Overview: HPQUANTSELECT Procedure

Subsections:

Quantile regression is a systematic statistical methodology for modeling conditional quantile functions of a response variable on explanatory covariate effects. Although modern quantile regression was introduced by Koenker and Bassett (1978), simple quantile regression that uses only the intercept as the explanatory effect has been practiced for much longer, because quantile is no more than a generalized notion for terms such as percentile, decile, quintile, and quartile. A conditional quantile of a response variable at quantile level $\tau $ denotes the value below which the proportion of the conditional response population is $\tau $. 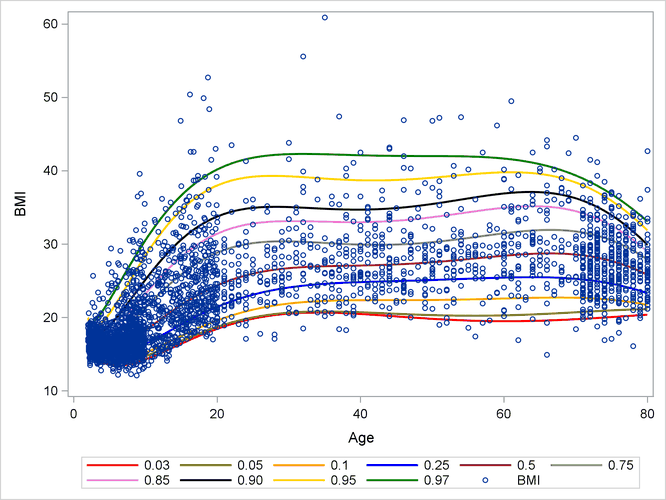Unlike linear regression, which exclusively focuses on the conditional mean, quantile regression can anatomize the entire response distribution and examine how the covariate effects influence the shape of the response distribution over the entire range of quantile levels $[0,1]$. Therefore, quantile regression provides a more comprehensive view of the regression relationship. Figure 14.1 shows an example of quantile regression that creates growth charts for the men’s body mass index (BMI) as quantile curves. Each entry in the legend shows the quantile level for the corresponding quantile curve. 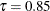For example, the curve whose quantile level $\tau =0.85$ corresponds to the 85th conditional percentile. For more information about the BMI example, see Growth Charts for Body Mass Index.

Figure 14.1: Growth Chart for Body Mass Index

Growth Chart for Body Mass Index


The HPQUANTSELECT procedure is a high-performance procedure that fits and performs effect selection for quantile regression analysis. PROC HPQUANTSELECT supports continuous variables, CLASS variables, and the interactions of these variables. PROC HPQUANTSELECT supports statistical inferences on quantile regression models with or without the assumption of independently and identically distributed (iid) errors. PROC HPQUANTSELECT also offers extensive capabilities for customizing the effect selection by using a wide variety of selection and stopping criteria.

PROC HPQUANTSELECT runs in either single-machine mode or distributed mode. NOTE: Distributed mode requires SAS High-Performance Statistics.