The RELIABILITY Procedure
- Overview
-
Getting Started
 Analysis of Right-Censored Data from a Single PopulationWeibull Analysis Comparing Groups of DataAnalysis of Accelerated Life Test DataWeibull Analysis of Interval Data with Common Inspection ScheduleLognormal Analysis with Arbitrary CensoringRegression ModelingRegression Model with Nonconstant ScaleRegression Model with Two Independent VariablesWeibull Probability Plot for Two Combined Failure ModesAnalysis of Recurrence Data on RepairsComparison of Two Samples of Repair DataAnalysis of Interval Age Recurrence DataAnalysis of Binomial DataThree-Parameter WeibullParametric Model for Recurrent Events DataParametric Model for Interval Recurrent Events Data
Analysis of Right-Censored Data from a Single PopulationWeibull Analysis Comparing Groups of DataAnalysis of Accelerated Life Test DataWeibull Analysis of Interval Data with Common Inspection ScheduleLognormal Analysis with Arbitrary CensoringRegression ModelingRegression Model with Nonconstant ScaleRegression Model with Two Independent VariablesWeibull Probability Plot for Two Combined Failure ModesAnalysis of Recurrence Data on RepairsComparison of Two Samples of Repair DataAnalysis of Interval Age Recurrence DataAnalysis of Binomial DataThree-Parameter WeibullParametric Model for Recurrent Events DataParametric Model for Interval Recurrent Events Data -
Syntax
 Primary StatementsSecondary StatementsGraphical Enhancement StatementsPROC RELIABILITY StatementANALYZE StatementBY StatementCLASS StatementDISTRIBUTION StatementEFFECTPLOT StatementESTIMATE StatementFMODE StatementFREQ StatementINSET StatementLOGSCALE StatementLSMEANS StatementLSMESTIMATE StatementMAKE StatementMCFPLOT StatementMODEL StatementNENTER StatementNLOPTIONS StatementPROBPLOT StatementRELATIONPLOT StatementSLICE StatementSTORE StatementTEST StatementUNITID Statement
Primary StatementsSecondary StatementsGraphical Enhancement StatementsPROC RELIABILITY StatementANALYZE StatementBY StatementCLASS StatementDISTRIBUTION StatementEFFECTPLOT StatementESTIMATE StatementFMODE StatementFREQ StatementINSET StatementLOGSCALE StatementLSMEANS StatementLSMESTIMATE StatementMAKE StatementMCFPLOT StatementMODEL StatementNENTER StatementNLOPTIONS StatementPROBPLOT StatementRELATIONPLOT StatementSLICE StatementSTORE StatementTEST StatementUNITID Statement -
Details
 Abbreviations and NotationTypes of Lifetime DataProbability DistributionsProbability PlottingNonparametric Confidence Intervals for Cumulative Failure ProbabilitiesParameter Estimation and Confidence IntervalsRegression Model Statistics Computed for Each Observation for Lifetime DataRegression Model Statistics Computed for Each Observation for Recurrent Events DataRecurrence Data from Repairable SystemsODS Table NamesODS Graphics
Abbreviations and NotationTypes of Lifetime DataProbability DistributionsProbability PlottingNonparametric Confidence Intervals for Cumulative Failure ProbabilitiesParameter Estimation and Confidence IntervalsRegression Model Statistics Computed for Each Observation for Lifetime DataRegression Model Statistics Computed for Each Observation for Recurrent Events DataRecurrence Data from Repairable SystemsODS Table NamesODS Graphics - References
Regression Model with Two Independent Variables
Meeker and Escobar (1998, p. 447) analyzed data from an accelerated test on the lifetimes of glass capacitors as a function of operating voltage and temperature. The following SAS statements create a SAS data set containing the data. There are four lifetimes for each of eight combinations and four censored observations after the fourth failure for each combination:
data glass;
input Temp Voltage @;
do i = 1 to 4;
cen = 0;
input Hours @; output;
end;
do i = 1 to 4;
cen = 1;
output;
end;
datalines;
170 200 439 904 1092 1105
170 250 572 690 904 1090
170 300 315 315 439 628
170 350 258 258 347 588
180 200 959 1065 1065 1087
180 250 216 315 455 473
180 300 241 315 332 380
180 350 241 241 435 455
;
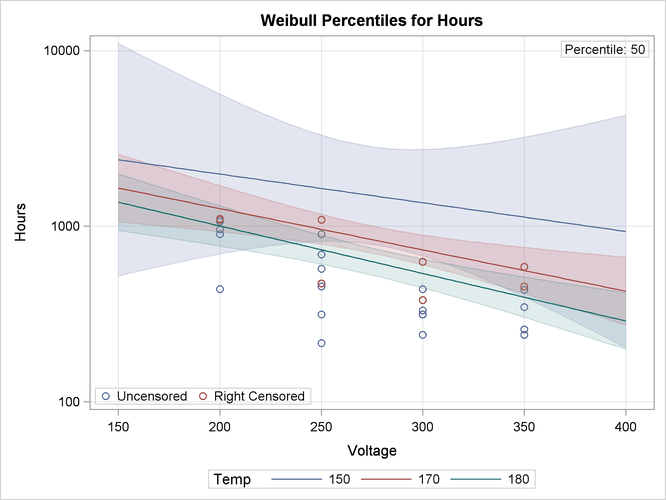
The following statements analyze the capacitor data. The MODEL statement fits a regression model with Temp and Voltage as independent variables. Parameter estimates from the fitted regression model are shown in Figure 17.24. An interaction term between Temp and Voltage is included. The PPLOT statement creates a Weibull probability plot shown in Figure 17.25 with all temperature-voltage combinations overlaid on the same plot. The regression model fit is also plotted. The RPLOT
statement creates the plot shown in Figure 17.26 of the data and Weibull distribution percentiles from the regression model as a function of voltage for values of temperature
of 150, 170, and 180:
proc reliability data = glass;
distribution Weibull;
model Hours*cen(1) = temp voltage temp * voltage;
pplot Hours*cen(1) = ( temp voltage ) / fit = model
overlay
noconf
lupper = 2000;
run;
proc reliability data = glass;
distribution Weibull;
model Hours*cen(1) = temp voltage temp * voltage;
rplot Hours*cen(1) = voltage / fit = regression(temp = 150, 170, 180)
plotfit;
run;
Figure 17.24: Parameter Estimates for Fitted Regression Model
| Weibull Parameter Estimates | ||||
|---|---|---|---|---|
| Parameter | Estimate | Standard Error |
Asymptotic Normal | |
| 95% Confidence Limits | ||||
| Lower | Upper | |||
| Intercept | 9.4135 | 10.5402 | -11.2449 | 30.0719 |
| Temp | -0.0062 | 0.0598 | -0.1235 | 0.1110 |
| Voltage | 0.0086 | 0.0374 | -0.0648 | 0.0820 |
| Temp*Voltage | -0.0001 | 0.0002 | -0.0005 | 0.0003 |
| EV Scale | 0.3624 | 0.0553 | 0.2687 | 0.4887 |
| Weibull Shape | 2.7593 | 0.4210 | 2.0461 | 3.7209 |
Figure 17.25: Probability Plot for Glass Capacitor Regression Model
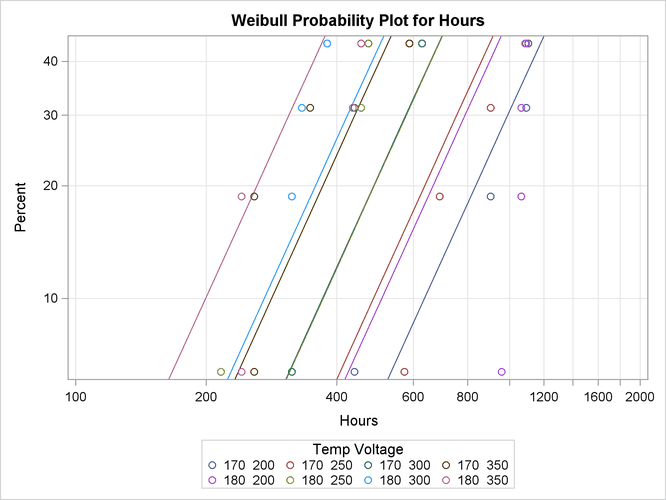
Figure 17.26: Plot of Data and Fitted Weibull Percentiles for Glass Capacitor Regression Model