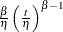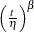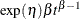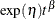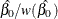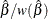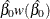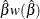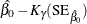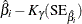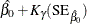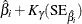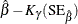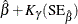The RELIABILITY Procedure
- Overview
-
Getting Started
 Analysis of Right-Censored Data from a Single PopulationWeibull Analysis Comparing Groups of DataAnalysis of Accelerated Life Test DataWeibull Analysis of Interval Data with Common Inspection ScheduleLognormal Analysis with Arbitrary CensoringRegression ModelingRegression Model with Nonconstant ScaleRegression Model with Two Independent VariablesWeibull Probability Plot for Two Combined Failure ModesAnalysis of Recurrence Data on RepairsComparison of Two Samples of Repair DataAnalysis of Interval Age Recurrence DataAnalysis of Binomial DataThree-Parameter WeibullParametric Model for Recurrent Events DataParametric Model for Interval Recurrent Events Data
Analysis of Right-Censored Data from a Single PopulationWeibull Analysis Comparing Groups of DataAnalysis of Accelerated Life Test DataWeibull Analysis of Interval Data with Common Inspection ScheduleLognormal Analysis with Arbitrary CensoringRegression ModelingRegression Model with Nonconstant ScaleRegression Model with Two Independent VariablesWeibull Probability Plot for Two Combined Failure ModesAnalysis of Recurrence Data on RepairsComparison of Two Samples of Repair DataAnalysis of Interval Age Recurrence DataAnalysis of Binomial DataThree-Parameter WeibullParametric Model for Recurrent Events DataParametric Model for Interval Recurrent Events Data -
Syntax
 Primary StatementsSecondary StatementsGraphical Enhancement StatementsPROC RELIABILITY StatementANALYZE StatementBY StatementCLASS StatementDISTRIBUTION StatementEFFECTPLOT StatementESTIMATE StatementFMODE StatementFREQ StatementINSET StatementLOGSCALE StatementLSMEANS StatementLSMESTIMATE StatementMAKE StatementMCFPLOT StatementMODEL StatementNENTER StatementNLOPTIONS StatementPROBPLOT StatementRELATIONPLOT StatementSLICE StatementSTORE StatementTEST StatementUNITID Statement
Primary StatementsSecondary StatementsGraphical Enhancement StatementsPROC RELIABILITY StatementANALYZE StatementBY StatementCLASS StatementDISTRIBUTION StatementEFFECTPLOT StatementESTIMATE StatementFMODE StatementFREQ StatementINSET StatementLOGSCALE StatementLSMEANS StatementLSMESTIMATE StatementMAKE StatementMCFPLOT StatementMODEL StatementNENTER StatementNLOPTIONS StatementPROBPLOT StatementRELATIONPLOT StatementSLICE StatementSTORE StatementTEST StatementUNITID Statement -
Details
 Abbreviations and NotationTypes of Lifetime DataProbability DistributionsProbability PlottingNonparametric Confidence Intervals for Cumulative Failure ProbabilitiesParameter Estimation and Confidence IntervalsRegression Model Statistics Computed for Each Observation for Lifetime DataRegression Model Statistics Computed for Each Observation for Recurrent Events DataRecurrence Data from Repairable SystemsODS Table NamesODS Graphics
Abbreviations and NotationTypes of Lifetime DataProbability DistributionsProbability PlottingNonparametric Confidence Intervals for Cumulative Failure ProbabilitiesParameter Estimation and Confidence IntervalsRegression Model Statistics Computed for Each Observation for Lifetime DataRegression Model Statistics Computed for Each Observation for Recurrent Events DataRecurrence Data from Repairable SystemsODS Table NamesODS Graphics - References
Recurrence Data from Repairable Systems
Failures in a system that can be repaired are sometimes modeled as recurrence data, or recurrent events data. When a repairable system fails, it is repaired and placed back in service. As a repairable system ages, it accumulates a
history of repairs and costs of repairs. The mean cumulative function (MCF) 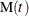 is defined as the population mean of the cumulative number (or cost) of repairs up until time t. You can use the RELIABILITY procedure to compute and plot nonparametric estimates and plots of the MCF for the number of
repairs or the cost of repairs. The Nelson (1995) confidence limits for the MCF are also computed and plotted. You can compute and plot estimates of the difference of two
MCFs and confidence intervals. This is useful for comparing the repair performance of two systems.
is defined as the population mean of the cumulative number (or cost) of repairs up until time t. You can use the RELIABILITY procedure to compute and plot nonparametric estimates and plots of the MCF for the number of
repairs or the cost of repairs. The Nelson (1995) confidence limits for the MCF are also computed and plotted. You can compute and plot estimates of the difference of two
MCFs and confidence intervals. This is useful for comparing the repair performance of two systems.
See Nelson (2002, 1995, 1988), Doganaksoy and Nelson (1998), and Nelson and Doganaksoy (1989) for discussions and examples of nonparametric analysis of recurrence data.
You can also fit a parametric model for recurrent event data and display the resulting model on a plot, along with nonparametric estimates of the MCF.
See Rigdon and Basu (2000), Tobias and Trindade (1995), and Meeker and Escobar (1998) for discussions of parametric models for recurrent events data.
Nonparametric Analysis
Recurrent Events Data with Exact Ages
See the section Analysis of Recurrence Data on Repairs and the section Comparison of Two Samples of Repair Data for examples of the analysis of recurrence data with exact ages.
Formulas for the MCF estimator 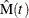 and the variance of the estimator Var
and the variance of the estimator Var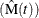 are given in Nelson (1995). Table 17.70 shows a set of artificial repair data from Nelson (1988). For each system, the data consist of the system and cost for each repair. If you want to compute the MCF for the number
of repairs, rather than cost of repairs, then you should set the cost equal to 1 for each repair. A plus sign (+) in place
of a cost indicates that the age is a censoring time. The repair history of each system ends with a censoring time.
are given in Nelson (1995). Table 17.70 shows a set of artificial repair data from Nelson (1988). For each system, the data consist of the system and cost for each repair. If you want to compute the MCF for the number
of repairs, rather than cost of repairs, then you should set the cost equal to 1 for each repair. A plus sign (+) in place
of a cost indicates that the age is a censoring time. The repair history of each system ends with a censoring time.
Table 17.70: System Repair Histories for Artificial Data
|
Unit |
(Age in Months, Cost in $100) |
|||
|---|---|---|---|---|
|
6 |
(5,$3) |
(12,$1) |
(12,+) |
|
|
5 |
(16,+) |
|||
|
4 |
(2,$1) |
(8,$1) |
(16,$2) |
(20,+) |
|
3 |
(18,$3) |
(29,+) |
||
|
2 |
(8,$2) |
(14,$1) |
(26,$1) |
(33,+) |
|
1 |
(19,$2) |
(39,$2) |
(42,+) |
|
Table 17.71 illustrates the calculation of the MCF estimate from the data in Table 17.70. The RELIABILITY procedure uses the following rules for computing the MCF estimates.
-
Order all events (repairs and censoring) by age from smallest to largest.
-
If the event ages of the same or different systems are equal, the corresponding data are sorted from the largest repair cost to the smallest. Censoring events always sort as smaller than repair events with equal ages.
-
When event ages and values of more than one system coincide, the corresponding data are sorted from the largest system identifier to the smallest. The system IDs can be numeric or character, but they are always sorted in ASCII order.
-
-
Compute the number of systems I in service at the current age as the number in service at the last repair time minus the number of censored units in the intervening times.
-
For each repair, compute the mean cost as the cost of the current repair divided by the number in service I.
-
Compute the MCF for each repair as the previous MCF plus the mean cost for the current repair.
Table 17.71: Calculation of MCF for Artificial Data
|
Number I in |
Mean |
|||
|---|---|---|---|---|
|
Event |
(Age,Cost) |
Service |
Cost |
MCF |
|
1 |
(2,$1) |
6 |
$1/6=0.17 |
0.17 |
|
2 |
(5,$3) |
6 |
$3/6=0.50 |
0.67 |
|
3 |
(8,$2) |
6 |
$2/6=0.33 |
1.00 |
|
4 |
(8,$1) |
6 |
$1/6=0.17 |
1.17 |
|
5 |
(12,$1) |
6 |
$1/6=0.17 |
1.33 |
|
6 |
(12,+) |
5 |
||
|
7 |
(14,$1) |
5 |
$1/5=0.20 |
1.53 |
|
8 |
(16,$2) |
5 |
$2/5=0.40 |
1.93 |
|
9 |
(16,+) |
4 |
||
|
10 |
(18,$3) |
4 |
$3/4=0.75 |
2.68 |
|
11 |
(19,$2) |
4 |
$2/4=0.50 |
3.18 |
|
12 |
(20,+) |
3 |
||
|
13 |
(26,$1) |
3 |
$1/3=0.33 |
3.52 |
|
14 |
(29,+) |
2 |
||
|
15 |
(33,+) |
1 |
||
|
16 |
(39,$2) |
1 |
$2/1=2.00 |
5.52 |
|
17 |
(42,+) |
0 |
If you specify the VARIANCE=NELSON option, the variance of the estimator of the MCF Var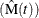 is computed as in Nelson (1995). If the VARIANCE=LAWLESS or VARMETHOD2 option is specified, the method of Lawless and Nadeau (1995) is used to compute the variance of the estimator of the MCF. This method is recommended if the number of systems or events
is large or if a FREQ statement is used to specify a frequency variable. If you do not specify a variance computation method,
the method of Lawless and Nadeau (1995) is used.
is computed as in Nelson (1995). If the VARIANCE=LAWLESS or VARMETHOD2 option is specified, the method of Lawless and Nadeau (1995) is used to compute the variance of the estimator of the MCF. This method is recommended if the number of systems or events
is large or if a FREQ statement is used to specify a frequency variable. If you do not specify a variance computation method,
the method of Lawless and Nadeau (1995) is used.
Default approximate two-sided 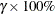 pointwise confidence limits for
pointwise confidence limits for 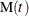 are computed as
are computed as
![\[ \mr{M}_{L}(t) = \hat{\mr{M}}(t) - K_{\gamma }\sqrt {\mbox{Var}(\hat{\mr{M}}(t))} \]](images/qcug_reliability0418.png)
![\[ \mr{M}_{U}(t) = \hat{\mr{M}}(t) + K_{\gamma }\sqrt {\mbox{Var}(\hat{\mr{M}}(t))} \]](images/qcug_reliability0419.png)
where 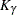 represents the
represents the 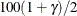 percentile of the standard normal distribution.
percentile of the standard normal distribution.
If you specify the LOGINTERVALS option in the MCFPLOT statement, alternative confidence intervals based on the asymptotic
normality of 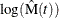 , rather than of
, rather than of 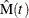 , are computed. Let
, are computed. Let
![\[ w = \exp \left[\frac{K_{\gamma }\sqrt {\mbox{Var}(\hat{\mr{M}}(t))}}{\hat{\mr{M}}(t)}\right] \]](images/qcug_reliability0422.png)
Then the limits are computed as
![\[ \mr{M}_{L}(t) = \frac{\hat{\mr{M}}(t)}{w} \]](images/qcug_reliability0423.png)
![\[ \mr{M}_{U}(t) = \hat{\mr{M}}(t)\times w \]](images/qcug_reliability0424.png)
These alternative limits are always positive, and can provide better coverage than the default limits when the MCF is known to be positive, such as for counts or for positive costs. They are not appropriate for MCF differences, and are not computed in this case.
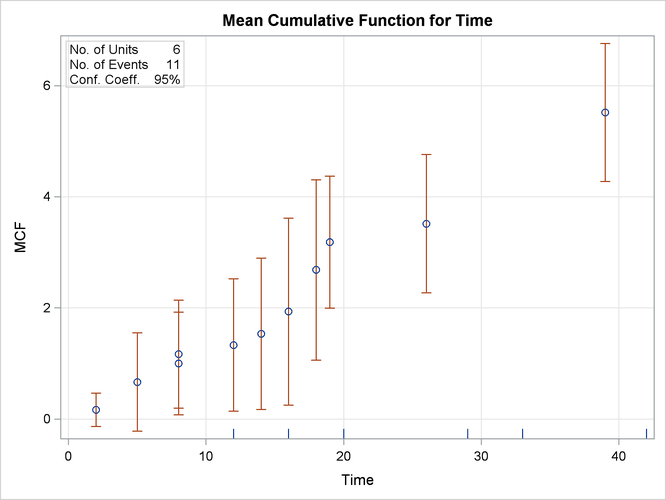
The following SAS statements create the tabular output shown in Figure 17.59 and the plot shown in Figure 17.60:
data Art; input Sysid $ Time Cost; datalines; sys1 19 2 sys1 39 2 sys1 42 -1 sys2 8 2 sys2 14 1 sys2 26 1 sys2 33 -1 sys3 18 3 sys3 29 -1 sys4 16 2 sys4 2 1 sys4 20 -1 sys4 8 1 sys5 16 -1 sys6 5 3 sys6 12 1 sys6 12 -1 ;
proc reliability data=Art; unitid Sysid; mcfplot Time*Cost(-1) ; run;
The first table in Figure 17.59 displays the input data set, the number of observations used in the analysis, the number of systems (units), and the number of repair events. The second table displays the system age, MCF estimate, standard error, approximate confidence limits, and system ID for each event.
Figure 17.59: PROC RELIABILITY Output for the Artificial Data
| Recurrence Data Analysis | |||||
|---|---|---|---|---|---|
| Age | Sample MCF | Standard Error |
95% Confidence Limits | Unit ID | |
| Lower | Upper | ||||
| 2.00 | 0.167 | 0.152 | -0.132 | 0.465 | sys4 |
| 5.00 | 0.667 | 0.451 | -0.218 | 1.551 | sys6 |
| 8.00 | 1.000 | 0.471 | 0.076 | 1.924 | sys2 |
| 8.00 | 1.167 | 0.495 | 0.196 | 2.138 | sys4 |
| 12.00 | 1.333 | 0.609 | 0.141 | 2.526 | sys6 |
| 14.00 | 1.533 | 0.695 | 0.172 | 2.895 | sys2 |
| 16.00 | 1.933 | 0.859 | 0.249 | 3.618 | sys4 |
| 18.00 | 2.683 | 0.828 | 1.061 | 4.306 | sys3 |
| 19.00 | 3.183 | 0.607 | 1.993 | 4.373 | sys1 |
| 26.00 | 3.517 | 0.634 | 2.274 | 4.759 | sys2 |
| 39.00 | 5.517 | 0.634 | 4.274 | 6.759 | sys1 |
Figure 17.60: MCF Plot for the Artificial Data
Recurrent Events Data with Ages Grouped into Intervals
Recurrence data are sometimes grouped into time intervals for convenience, or to reduce the number of data records to be stored and analyzed. Interval recurrence data consist of the number of recurrences and the number of censored units in each time interval.
You can use PROC RELIABILITY to compute and plot MCFs and MCF differences for interval data. Formulas for the MCF estimator
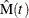 and the variance of the estimator Var
and the variance of the estimator Var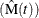 for interval data, as well as examples and interpretations, are given in Nelson (2002, chapter 5). These calculations apply only to the number of recurrences, and not to cost.
for interval data, as well as examples and interpretations, are given in Nelson (2002, chapter 5). These calculations apply only to the number of recurrences, and not to cost.
Let 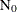 be the total number of units,
be the total number of units, 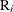 the number of recurrences in interval i,
the number of recurrences in interval i, 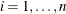 , and
, and 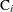 the number of units censored into interval i. Then
the number of units censored into interval i. Then 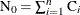 and the number entering interval i is
and the number entering interval i is 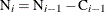 with
with 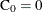 . The MCF estimate for interval i is
. The MCF estimate for interval i is 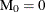 ,
,
![\[ \mr{M}_ i = \mr{M}_{i-1} + \frac{\mr{R}_ i}{\mr{N}_ i - 0.5 \mr{C}_ i} \]](images/qcug_reliability0433.png)
The denominator 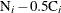 approximates the number at risk in interval i, and treats the censored units as if they were censored halfway through the interval. Since no censored units are likely
to have ages lasting through the entire last interval, the MCF estimate for the last interval is likely to be biased. A footnote
is printed in the tabular output as a reminder of this bias for the last interval.
approximates the number at risk in interval i, and treats the censored units as if they were censored halfway through the interval. Since no censored units are likely
to have ages lasting through the entire last interval, the MCF estimate for the last interval is likely to be biased. A footnote
is printed in the tabular output as a reminder of this bias for the last interval.
See the section Analysis of Interval Age Recurrence Data for an example of interval recurrence data analysis.
Comparison of Two Groups of Recurrent Events Data
If you specify a group variable in an MCFPLOT statement, and the group variable has only two levels representing two groups of data, then there are two ways to compare the MCFs of the two groups for equality.
If you specify the MCFDIFF
option in the MCFPLOT
statement, estimates of the difference between two MCFs 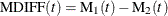 and the variance of the estimator are computed and plotted as in Doganaksoy and Nelson (1998). Confidence limits for the MCF difference function are computed in the same way as for the MCF, by using the variance of
the MCF difference function estimator. If the confidence limits do not enclose zero at any time point, then the statistical
hypothesis that the two MCFs are equal at all times is rejected.
and the variance of the estimator are computed and plotted as in Doganaksoy and Nelson (1998). Confidence limits for the MCF difference function are computed in the same way as for the MCF, by using the variance of
the MCF difference function estimator. If the confidence limits do not enclose zero at any time point, then the statistical
hypothesis that the two MCFs are equal at all times is rejected.
Cook and Lawless (2007, section 3.7.5) describe statistical tests based on weighted sums of sample differences in the MCFs of the two groups. These tests, similar to log-rank tests for survival data, are computed and displayed in the "Tests for Equality of Mean Functions" table. Two cases are computed, corresponding to different weight functions in the test statistic. The "constant" case is powerful in cases where the two MCFs are approximately proportional. The "linear" case is more powerful for cases where the MCFs are not proportional, but do not cross.
These methods are not available for grouped data, as described in Recurrent Events Data with Ages Grouped into Intervals.
Parametric Models for Recurrent Events Data
The parametric models used for recurrent events data in PROC RELIABILITY are called Poisson process models. Some important features of these models are summarized below. See, for example, Rigdon and Basu (2000) and Meeker and Escobar (1998) for a full mathematical description of these models. See Cook and Lawless (2007) for a general discussion of maximum likelihood estimation in Poisson processes. Abernethy (2006) and US Army (2000) provide examples of the application of Poisson process models to system reliability.
Let 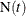 be the number of events up to time t, and let
be the number of events up to time t, and let 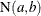 be the number of events in the interval
be the number of events in the interval ![$(a,b]$](images/qcug_reliability0438.png) . Then, for a Poisson process,
. Then, for a Poisson process,
-
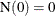 .
.
-
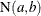 and
and 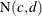 are statistically independent if
are statistically independent if 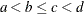 .
.
-
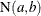 is a Poisson random variable with mean
is a Poisson random variable with mean 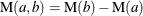 where
where 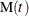 is the mean number of failures up to time t.
is the mean number of failures up to time t. 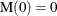 .
.
Poisson processes are characterized by their cumulative mean function 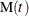 , or equivalently by their intensity, rate, or rate of occurrence of failure (ROCOF) function
, or equivalently by their intensity, rate, or rate of occurrence of failure (ROCOF) function 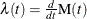 , so that
, so that
![\[ \mr{M}(a,b)=\mr{M}(b)-\mr{M}(a) = \int _{a}^{b}\lambda (t)dt \]](images/qcug_reliability0445.png)
Poisson processes are parameterized through their mean and rate functions. The RELIABILITY procedure provides the Poisson process models shown in Table 17.72.
Table 17.72: Models and Parameters for Recurrent Events Data
|
Model |
Intensity Function |
Mean Function |
|---|---|---|
|
Crow-AMSAA |
|
|
|
Homogeneous |
|
|
|
Log-linear |
|
|
|
Power |
|
|
|
Proportional intensity |
|
|
For a homogeneous Poisson process, the intensity function is a constant; that is, the rate of failures does not change with time. For the other models, the rate function can change with time, so that a rate of failures that increases or decreases with time can be modeled. These models are called non-homogeneous Poisson processes.
In the RELIABILITY procedure, you specify a Poisson model with a DISTRIBUTION statement and a MODEL statement. You must also specify additional statements, depending on whether failure times are observed exactly, or observed to occur in time intervals. These statements are explained in the sections Recurrent Events Data with Exact Event Ages, Recurrent Events Data with Interval Event Ages, and MODEL Statement. The DISTRIBUTION statement specifications for the models described in Table 17.72 are summarized in Table 17.73.
Table 17.73: DISTRIBUTION Statement Specification for Recurrent Events Data Models
|
Model |
DISTRIBUTION Statement Value |
|---|---|
|
Crow-AMSAA |
NHPP(CA) |
|
Homogeneous |
HPP |
|
Log-linear |
NHPP(LOG) |
|
Power |
NHPP(POW) |
|
Proportional intensity |
NHPP(PROP) |
For each of the models, you can specify a regression model for the parameter 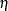 in Table 17.72 for the
in Table 17.72 for the 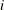 th observation as
th observation as
![\[ \eta _{i} = \beta _{0} + \beta _{1}x_{i1} + \ldots \]](images/qcug_reliability0406.png)
where 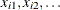 are regression coefficients specified as described in the section MODEL Statement. The parameter
are regression coefficients specified as described in the section MODEL Statement. The parameter 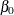 is labeled
is labeled Intercept in the printed output, and the parameter 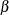 in Table 17.72 is labeled
in Table 17.72 is labeled Shape. If no regression coefficients are specified, Intercept represents the parameter 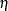 in Table 17.72.
in Table 17.72.
Model parameters are estimated by maximizing the log-likelihood function, which is equivalent to maximizing the likelihood
function. The sections Recurrent Events Data with Exact Event Ages and Recurrent Events Data with Interval Event Ages contain descriptions of the form of the log likelihoods for the different models. An estimate of the covariance matrix of
the maximum likelihood estimators (MLEs) of the parameters 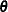 is given by the inverse of the negative of the matrix of second derivatives of the log likelihood, evaluated at the final
parameter estimates:
is given by the inverse of the negative of the matrix of second derivatives of the log likelihood, evaluated at the final
parameter estimates:
![\[ \bSigma = [\sigma _{ij}] = -\mb{H}^{-1} = -\left[ \frac{\partial ^{2}LL}{\partial \theta _{i}\partial \theta _{j}} \right]^{-1}_{\btheta =\hat{\btheta }} \]](images/qcug_reliability0458.png)
The negative of the matrix of second derivatives is called the observed Fisher information matrix. The diagonal term 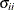 is an estimate of the variance of
is an estimate of the variance of 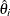 . Estimates of standard errors of the MLEs are provided by
. Estimates of standard errors of the MLEs are provided by
![\[ \mr{SE}_{\theta _{i}} = \sqrt {\sigma _{ii}} \]](images/qcug_reliability0212.png)
An estimator of the correlation matrix is
![\[ \mb{R} = \left[ \frac{\sigma _{ij}}{\sqrt {\sigma _{ii}\sigma _{jj}}} \right] \]](images/qcug_reliability0213.png)
Wald-type confidence intervals are computed for the model parameters as described in Table 17.74. Wald intervals use asymptotic normality of maximum likelihood estimates to compute approximate confidence intervals. If
a parameter must be greater than zero, then an approximation based on the asymptotic normality of the logarithm of the parameter
estimate is often more accurate, and the lower endpoint is strictly positive. The intercept term 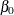 in an intercept-only power NHPP model with no other regression parameters represents
in an intercept-only power NHPP model with no other regression parameters represents 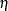 in Table 17.72, and is a model parameter that must be strictly positive. Also, the shape parameter for the power and proportional intensity
models, represented by
in Table 17.72, and is a model parameter that must be strictly positive. Also, the shape parameter for the power and proportional intensity
models, represented by 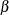 in Table 17.72, must be strictly positive. In these cases, formula 7.11 of Meeker and Escobar (1998, p. 163) is used in Table 17.74 to compute confidence limits.
in Table 17.72, must be strictly positive. In these cases, formula 7.11 of Meeker and Escobar (1998, p. 163) is used in Table 17.74 to compute confidence limits.
Table 17.74 shows the method of computation of approximate two-sided 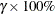 confidence limits for model parameters. The default value of confidence is
confidence limits for model parameters. The default value of confidence is 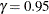 . Other values of confidence are specified using the CONFIDENCE= option. In Table 17.74,
. Other values of confidence are specified using the CONFIDENCE= option. In Table 17.74, 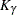 represents the
represents the 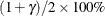 percentile of the standard normal distribution, and
percentile of the standard normal distribution, and ![$w(\hat{\theta })=\exp [K_{\gamma }\mr{(SE}_{\hat{\theta }})/\hat{\theta }]$](images/qcug_reliability0459.png) .
.
Table 17.74: NHPP Model Parameter Confidence Limit Computation
|
Parameters |
||||
|---|---|---|---|---|
|
Model |
Intercept |
Regression |
Shape |
|
|
Parameters |
||||
|
Crow-AMSAA |
||||
|
Intercept-only model |
||||
|
|
|
|
||
|
|
|
|
||
|
Regression model |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Homogeneous |
||||
|
|
|
|
||
|
|
|
|
||
|
Log-linear |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Power |
||||
|
Intercept-only model |
||||
|
|
|
|
||
|
|
|
|
||
|
Regression model |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Proportional intensity |
||||
|
|
|
|
|
|
|
|
|
|
|
|
You can request that profile likelihood confidence intervals for model parameters be computed instead of Wald intervals with the LRCL option in the MODEL statement.
Confidence limits for the mean and intensity functions for plots that are created with the MCFPLOT statement and for the table
that is created with the OBSTATS option in the MODEL statement are computed by using the delta method. See Meeker and Escobar
(1998, Appendix B) for a full explanation of this method. If 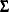 represents the covariance matrix of the estimates of the parameters
represents the covariance matrix of the estimates of the parameters 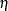 and
and 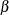 in Table 17.72, then the variance of the mean or intensity function estimate is given by
in Table 17.72, then the variance of the mean or intensity function estimate is given by
![\[ \mr{V} = [\frac{\partial {g}}{\partial {\eta }} \frac{\partial {g}}{\partial {\beta }}] \bSigma [\frac{\partial {g}}{\partial {\eta }} \frac{\partial {g}}{\partial {\beta }}]’ \]](images/qcug_reliability0472.png)
where 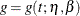 represents either the mean function or the intensity function in Table 17.72. Since both of these functions must be positive, formula 7.11 of Meeker and Escobar (1998, p. 163) is used to compute confidence limits, using the standard error
represents either the mean function or the intensity function in Table 17.72. Since both of these functions must be positive, formula 7.11 of Meeker and Escobar (1998, p. 163) is used to compute confidence limits, using the standard error 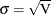 . For regression models, the full covariance matrix of all the regression parameter estimates and the parameter
. For regression models, the full covariance matrix of all the regression parameter estimates and the parameter 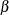 is used to compute
is used to compute 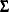 .
.
Tests of Trend
For the nonhomogeneous models in Table 17.72, you can request a test for a homogeneous Poisson process by specifying the HPPTEST
option in the MODEL statement. In this case the test is a likelihood ratio test for 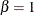 for the power, Crow-AMSAA, and proportional intensity models, and
for the power, Crow-AMSAA, and proportional intensity models, and 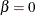 for the log-linear model.
for the log-linear model.
You can request other tests of trend by using the TREND= option in the MODEL statement. These tests are not available for the kind of grouped data that are described in the section Recurrent Events Data with Interval Event Ages. See Lindqvist and Doksum (2003), Kvaloy and Lindqvist (1998), and Meeker and Escobar (1998) for a discussion of these kinds of tests.
Let there be m independent systems observed, and let 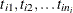 be the times of observed events for system i. Let the last time of observation of system i be
be the times of observed events for system i. Let the last time of observation of system i be 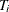 , with
, with 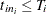 . The following test statistics can be computed. These are extended versions of trend tests for a single system, and they
allow valid tests for HPP versus NHPP even if the intensities vary from system to system.
. The following test statistics can be computed. These are extended versions of trend tests for a single system, and they
allow valid tests for HPP versus NHPP even if the intensities vary from system to system.
-
Military Handbook (MH)
![\[ \mr{MH} = 2\sum _{i=1}^{m}\sum _{j=1}^{n_ i}\log \left(\frac{T_ i}{t_{ij}}\right) \]](images/qcug_reliability0479.png)
The asymptotic distribution of
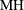 is the chi-square with
is the chi-square with 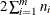 degrees of freedom. This test statistic is powerful for testing HPP versus NHPP in the power law model.
degrees of freedom. This test statistic is powerful for testing HPP versus NHPP in the power law model.
-
Laplace (LA)
![\[ \mr{LA} = \frac{\sum _{i=1}^{m}\sum _{j=1}^{n_ i}(t_{ij} - \frac{1}{2}T_ i)}{\sqrt {{\frac{1}{12}\sum _{i=1}^{m}n_ iT_ i^2}}} \]](images/qcug_reliability0482.png)
The asymptotic distribution of
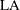 is the standard normal. This test statistic is powerful for testing HPP versus NHPP in a log-linear model.
is the standard normal. This test statistic is powerful for testing HPP versus NHPP in a log-linear model.
-
Lewis-Robinson (LR)
Let
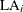 be the Laplace test statistic for system i,
be the Laplace test statistic for system i,
![\[ \mr{LA}_ i = \frac{\sum _{j=1}^{n_ i}(t_{ij} - \frac{1}{2}T_ i ) }{\sqrt {\frac{1}{12}n_ i} } \]](images/qcug_reliability0485.png)
The extended Lewis-Robinson test statistic is defined as
![\[ \mr{LR} = \sum _{i=1}^{m} \frac{\bar{X}_ i}{\sigma _ i}\mr{LA}_ i \]](images/qcug_reliability0486.png)
where
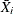 and
and 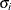 are the estimated mean and standard deviation of the event interarrival times for system i. The asymptotic distribution of
are the estimated mean and standard deviation of the event interarrival times for system i. The asymptotic distribution of 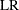 is the standard normal. This test statistic is powerful for testing HPP versus NHPP in a log-linear model.
is the standard normal. This test statistic is powerful for testing HPP versus NHPP in a log-linear model.
INEST Data Set for Recurrent Events Models
You can specify a SAS data set to set lower bounds, upper bounds, equality constraints, or initial values for estimating
the intercept and shape parameters of the models in Table 17.72 by using the INEST=
option in the MODEL statement. The data set must contain a variable named _TYPE_ that specifies the action that you want to take in the iterative estimation process, and some combination of variables named
_INTERCEPT_ and _SHAPE_ that represent the distribution parameters. If BY processing is used, the INEST= data set should also include the BY variables,
and there must be at least one observation for each BY group.
The possible values of _TYPE_ and corresponding actions are summarized in Table 17.75.
Table 17.75: _TYPE_ Variable Values
|
Value of |
Action |
|---|---|
|
LB |
Lower bound |
|
UB |
Upper bound |
|
EQ |
Equality |
|
PARMS |
Initial value |
For example, you can use the INEST data set In created by the following SAS statements to specify an equality constraint for the shape parameter. The data set In specifies that the shape parameter be constrained to be 1.5. Since the variable _Intercept_ is set to missing, no action is taken for it, and this variable could be omitted from the data set.
data In ; input _Type_$ 1-5 _Intercept_ _Shape_; datalines; eq . 1.5 ;
Recurrent Events Data with Exact Event Ages
Let there be m independent systems observed, and let 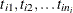 be the times of observed events for system i. Let the last time of observation of system i be
be the times of observed events for system i. Let the last time of observation of system i be 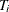 , with
, with 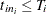 .
.
If there are no regression parameters in the model, or there are regression parameters and they are constant for each system, then the log-likelihood function is
![\[ LL = \sum _{i=1}^{m}\{ \sum _{j=1}^{n_ i}[\log (\lambda (t_{ij})] - \mr{M}(T_ i)\} \]](images/qcug_reliability0490.png)
If there are regression parameters that can change over time for individual systems, the RELIABILITY procedure uses the convention
that a covariate value specified at a given event time takes effect immediately after the event time; that is, the value of
a covariate used at an event time is the value specified at the previous event time. The value used at the first event time
is the value specified at that event time. You can establish a different value for the first event time by specifying a zero
cost event previous to the first actual event. The zero cost event is not used in the analysis, but it is used to establish
a covariate value for the next event time. The covariate value used at the end time 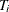 is the value established at the last event time.
is the value established at the last event time.
With these conventions, the log likelihood is
![\[ LL = \sum _{i=1}^{m}\{ \sum _{j=1}^{n_ i}[\log (\lambda (t_{ij}) - (\mr{M}(t_{ij})-\mr{M}(t_{i,j-1})] - (\mr{M}(T_ i)-\mr{M}(t_{in_ i})\} \]](images/qcug_reliability0491.png)
with 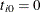 for each
for each 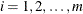 . Note that this log likelihood reduces to the previous log likelihood if covariate values do not change over time for each
system.
. Note that this log likelihood reduces to the previous log likelihood if covariate values do not change over time for each
system.
In order to specify a parametric model for recurrence data with exact event times, you specify the event times, end of observation times, and regression model, if any, with a MODEL statement, as described in the section MODEL Statement. In addition, you specify a variable that uniquely identifies each system with a UNITID statement. See the section Parametric Model for Recurrent Events Data for an example of fitting a parametric recurrent events model to data with exact recurrence times.
Recurrent Events Data with Interval Event Ages
If n independent and statistically identical systems are observed in the time interval ![$(t_ a, t_ b]$](images/qcug_reliability0494.png) , then the number r of events that occur in the interval is a Poisson random variable with mean
, then the number r of events that occur in the interval is a Poisson random variable with mean ![$n\mr{M}(t_ a,t_ b)=n[\mr{M}(t_ a)-\mr{M}(t_ b)]$](images/qcug_reliability0495.png) , where
, where 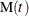 is the cumulative mean function for an individual system.
is the cumulative mean function for an individual system.
Let ![$(t_0, t_1], (t_1, t_2], \ldots , (t_{m-1}, t_ m]$](images/qcug_reliability0496.png) be nonoverlapping time intervals for which
be nonoverlapping time intervals for which  events are observed among the
events are observed among the 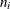 systems observed in time interval
systems observed in time interval ![$(t_{i-1}, t_ i]$](images/qcug_reliability0498.png) . The parameters in the mean function
. The parameters in the mean function 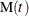 are estimated by maximizing the log likelihood
are estimated by maximizing the log likelihood
![\[ LL = \sum _{i=1}^ m[r_ i\log (n_ i) + r_ i\log (\mr{M}(t_{i-1},t_ i)) - n_ i\mr{M}(t_{i-1},t_ i) - \log (r_ i!)] \]](images/qcug_reliability0499.png)
The time intervals do not have to be of the same length, and they do not have to be adjacent, although the preceding formula shows them as adjacent.
If you have data from groups of systems to which you are fitting a regression model (for example, to model the effects of different manufacturing lines or different vendors), the time intervals in the different groups do not have to coincide. The only requirement is that the data in the different groups be independent; for example, you cannot have data from the same systems in two different groups.
In order to specify a parametric model for interval recurrence data, you specify the time intervals and regression model,
if any, with a MODEL
statement, as described in the section MODEL Statement. In addition, you specify a variable that contains the number 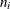 of systems under observation in time interval i with an NENTER
statement, and the number of events
of systems under observation in time interval i with an NENTER
statement, and the number of events  observed with a FREQ
statement. See the section Parametric Model for Interval Recurrent Events Data for an example of fitting a parametric recurrent events model to data with interval recurrence times.
observed with a FREQ
statement. See the section Parametric Model for Interval Recurrent Events Data for an example of fitting a parametric recurrent events model to data with interval recurrence times.
Duane Plots
A Duane plot is defined as a graph of the quantity 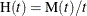 versus t, where
versus t, where 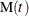 is the MCF. The graph axes are usually both on the log scale, so that if
is the MCF. The graph axes are usually both on the log scale, so that if 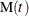 is the power law type in Table 17.72, a linear graph is produced. Duane plots are traditionally used as a visual assessment of the goodness of fit of a power
law model. You should exercise caution in using Duane plots, because even if the underlying model is a power law process,
a nonlinear Duane plot can result. See Rigdon and Basu (2000, section 4.1.1) for a discussion of Duane plots. You can create a Duane plot by specifying the DUANE
option in the MCFPLOT
statement. A scatter plot of nonparametric estimates of
is the power law type in Table 17.72, a linear graph is produced. Duane plots are traditionally used as a visual assessment of the goodness of fit of a power
law model. You should exercise caution in using Duane plots, because even if the underlying model is a power law process,
a nonlinear Duane plot can result. See Rigdon and Basu (2000, section 4.1.1) for a discussion of Duane plots. You can create a Duane plot by specifying the DUANE
option in the MCFPLOT
statement. A scatter plot of nonparametric estimates of 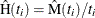 versus
versus 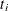 is created on a log-log scale, where
is created on a log-log scale, where 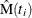 are the nonparametric estimates of the MCF that are described in the section Nonparametric Analysis. If you specify a parametric model with the FIT=MODEL
option in the MCFPLOT
statement, the corresponding parametric estimate of
are the nonparametric estimates of the MCF that are described in the section Nonparametric Analysis. If you specify a parametric model with the FIT=MODEL
option in the MCFPLOT
statement, the corresponding parametric estimate of 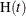 is plotted on the same graph as the scatter plot.
is plotted on the same graph as the scatter plot.
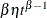
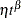
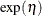
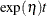
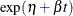
![$\frac{\exp (\eta )}{\beta }[\exp (\beta t)-1]$](images/qcug_reliability0451.png)