The RELIABILITY Procedure
- Overview
-
Getting Started
 Analysis of Right-Censored Data from a Single PopulationWeibull Analysis Comparing Groups of DataAnalysis of Accelerated Life Test DataWeibull Analysis of Interval Data with Common Inspection ScheduleLognormal Analysis with Arbitrary CensoringRegression ModelingRegression Model with Nonconstant ScaleRegression Model with Two Independent VariablesWeibull Probability Plot for Two Combined Failure ModesAnalysis of Recurrence Data on RepairsComparison of Two Samples of Repair DataAnalysis of Interval Age Recurrence DataAnalysis of Binomial DataThree-Parameter WeibullParametric Model for Recurrent Events DataParametric Model for Interval Recurrent Events Data
Analysis of Right-Censored Data from a Single PopulationWeibull Analysis Comparing Groups of DataAnalysis of Accelerated Life Test DataWeibull Analysis of Interval Data with Common Inspection ScheduleLognormal Analysis with Arbitrary CensoringRegression ModelingRegression Model with Nonconstant ScaleRegression Model with Two Independent VariablesWeibull Probability Plot for Two Combined Failure ModesAnalysis of Recurrence Data on RepairsComparison of Two Samples of Repair DataAnalysis of Interval Age Recurrence DataAnalysis of Binomial DataThree-Parameter WeibullParametric Model for Recurrent Events DataParametric Model for Interval Recurrent Events Data -
Syntax
 Primary StatementsSecondary StatementsGraphical Enhancement StatementsPROC RELIABILITY StatementANALYZE StatementBY StatementCLASS StatementDISTRIBUTION StatementEFFECTPLOT StatementESTIMATE StatementFMODE StatementFREQ StatementINSET StatementLOGSCALE StatementLSMEANS StatementLSMESTIMATE StatementMAKE StatementMCFPLOT StatementMODEL StatementNENTER StatementNLOPTIONS StatementPROBPLOT StatementRELATIONPLOT StatementSLICE StatementSTORE StatementTEST StatementUNITID Statement
Primary StatementsSecondary StatementsGraphical Enhancement StatementsPROC RELIABILITY StatementANALYZE StatementBY StatementCLASS StatementDISTRIBUTION StatementEFFECTPLOT StatementESTIMATE StatementFMODE StatementFREQ StatementINSET StatementLOGSCALE StatementLSMEANS StatementLSMESTIMATE StatementMAKE StatementMCFPLOT StatementMODEL StatementNENTER StatementNLOPTIONS StatementPROBPLOT StatementRELATIONPLOT StatementSLICE StatementSTORE StatementTEST StatementUNITID Statement -
Details
 Abbreviations and NotationTypes of Lifetime DataProbability DistributionsProbability PlottingNonparametric Confidence Intervals for Cumulative Failure ProbabilitiesParameter Estimation and Confidence IntervalsRegression Model Statistics Computed for Each Observation for Lifetime DataRegression Model Statistics Computed for Each Observation for Recurrent Events DataRecurrence Data from Repairable SystemsODS Table NamesODS Graphics
Abbreviations and NotationTypes of Lifetime DataProbability DistributionsProbability PlottingNonparametric Confidence Intervals for Cumulative Failure ProbabilitiesParameter Estimation and Confidence IntervalsRegression Model Statistics Computed for Each Observation for Lifetime DataRegression Model Statistics Computed for Each Observation for Recurrent Events DataRecurrence Data from Repairable SystemsODS Table NamesODS Graphics - References
Parameter Estimation and Confidence Intervals
Maximum Likelihood Estimation
Maximum likelihood estimation of the parameters of a statistical model involves maximizing the likelihood or, equivalently, the log likelihood with respect to the parameters. The parameter values at which the maximum occurs are the maximum likelihood estimates of the model parameters. The likelihood is a function of the parameters and of the data.
Let ![]() be the observations in a random sample, including the failures and censoring times (if the data are censored). Let
be the observations in a random sample, including the failures and censoring times (if the data are censored). Let ![]() be the probability density of failure time,
be the probability density of failure time, ![]() be the reliability function, and
be the reliability function, and ![]() be the cumulative distribution function, where
be the cumulative distribution function, where ![]() is the vector of parameters to be estimated,
is the vector of parameters to be estimated, ![]() . The probability density, reliability function, and CDF are determined by the specific distribution selected as a model for
the data. The log likelihood is defined as
. The probability density, reliability function, and CDF are determined by the specific distribution selected as a model for
the data. The log likelihood is defined as
|
|
|
|
|
|
|
|
where
-
 is the sum over failed units
is the sum over failed units
-
 is the sum over right-censored units
is the sum over right-censored units
-
 is the sum over left-censored units
is the sum over left-censored units
-
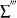 is the sum over interval-censored units
is the sum over interval-censored units
and ![]() is the interval in which the ith unit is interval censored. Only the sums appropriate to the type of censoring in the data are included when the preceding
equation is used.
is the interval in which the ith unit is interval censored. Only the sums appropriate to the type of censoring in the data are included when the preceding
equation is used.
The RELIABILITY procedure maximizes the log likelihood with respect to the parameters ![]() by using a Newton-Raphson algorithm. The Newton-Raphson algorithm is a recursive method for computing the maximum of a function.
On the rth iteration, the algorithm updates the parameter vector
by using a Newton-Raphson algorithm. The Newton-Raphson algorithm is a recursive method for computing the maximum of a function.
On the rth iteration, the algorithm updates the parameter vector ![]() with
with
|
|
where ![]() is the Hessian (second derivative) matrix, and
is the Hessian (second derivative) matrix, and ![]() is the gradient (first derivative) vector of the log-likelihood function, both evaluated at the current value of the parameter
vector. That is,
is the gradient (first derivative) vector of the log-likelihood function, both evaluated at the current value of the parameter
vector. That is,
|
|
and
|
|
Iteration continues until the parameter estimates converge. The convergence criterion is
|
|
|
|
|
|
for all ![]() where c is the convergence criterion. The default value of c is
where c is the convergence criterion. The default value of c is ![]() , and it can be specified with the CONVERGE= option in the MODEL, PROBPLOT, RELATIONPLOT, and ANALYZE statements.
, and it can be specified with the CONVERGE= option in the MODEL, PROBPLOT, RELATIONPLOT, and ANALYZE statements.
After convergence by the preceding criterion, the quantity
|
|
is computed. If ![]() then a warning is printed that the algorithm did not converge.
then a warning is printed that the algorithm did not converge. ![]() is called the relative Hessian convergence criterion. The default value of d is 0.0001. You can specify other values for d with the CONVH= option. The relative Hessian criterion is useful in detecting the occasional case where no progress can be
made in increasing the log likelihood, yet the gradient g is not zero.
is called the relative Hessian convergence criterion. The default value of d is 0.0001. You can specify other values for d with the CONVH= option. The relative Hessian criterion is useful in detecting the occasional case where no progress can be
made in increasing the log likelihood, yet the gradient g is not zero.
A location-scale model has a CDF of the form
|
|
where ![]() is the location parameter,
is the location parameter, ![]() is the scale parameter, and G is a standardized form
is the scale parameter, and G is a standardized form ![]() of the cumulative distribution function. The parameter vector is
of the cumulative distribution function. The parameter vector is ![]() =(
=(![]()
![]() ). It is more convenient computationally to maximize log likelihoods that arise from location-scale models. If you specify
a distribution from Table 16.57 that is not a location-scale model, it is transformed to a location-scale model by taking the natural (base e) logarithm of the response. If you specify the lognormal base 10 distribution, the logarithm (base 10) of the response is
used. The Weibull, lognormal, and log-logistic distributions in Table 16.57 are not location-scale models. Table 16.58 shows the corresponding location-scale models that result from taking the logarithm of the response.
). It is more convenient computationally to maximize log likelihoods that arise from location-scale models. If you specify
a distribution from Table 16.57 that is not a location-scale model, it is transformed to a location-scale model by taking the natural (base e) logarithm of the response. If you specify the lognormal base 10 distribution, the logarithm (base 10) of the response is
used. The Weibull, lognormal, and log-logistic distributions in Table 16.57 are not location-scale models. Table 16.58 shows the corresponding location-scale models that result from taking the logarithm of the response.
Maximum likelihood is the default method of estimating the location and scale parameters in the MODEL, PROBPLOT, RELATIONPLOT,
and ANALYZE statements. If the Weibull distribution is specified, the logarithms of the responses are used to obtain maximum
likelihood estimates (![]()
![]() ) of the location and scale parameters of the extreme value distribution. The maximum likelihood estimates (
) of the location and scale parameters of the extreme value distribution. The maximum likelihood estimates (![]() ,
, ![]() ) of the Weibull scale and shape parameters are computed as
) of the Weibull scale and shape parameters are computed as ![]() and
and ![]() .
.
Three-Parameter Weibull
The parameters of the three-parameter Weibull distribution are estimated by maximizing the log likelihood function. The threshold
parameter ![]() must be less than the minimum failure time
must be less than the minimum failure time ![]() , unless
, unless ![]() , in which case,
, in which case, ![]() can be equal to
can be equal to ![]() . The RELIABILITY procedure sets a default upper bound of
. The RELIABILITY procedure sets a default upper bound of ![]() for the threshold in the iterative estimation computations and a default lower bound of 0.0. You can set different bounds
by specifying an INEST data set as described in the section INEST Data Set for the Three-Parameter Weibull.
for the threshold in the iterative estimation computations and a default lower bound of 0.0. You can set different bounds
by specifying an INEST data set as described in the section INEST Data Set for the Three-Parameter Weibull.
If the shape parameter ![]() is less than one, then the density function in Table 16.57 has a singularity at
is less than one, then the density function in Table 16.57 has a singularity at ![]() , and the log likelihood is unbounded above as the threshold parameter approaches the minimum failure time
, and the log likelihood is unbounded above as the threshold parameter approaches the minimum failure time ![]() . For any fixed
. For any fixed ![]() , maximum likelihood estimates of the scale and shape parameters
, maximum likelihood estimates of the scale and shape parameters ![]() and
and ![]() exist. If
exist. If ![]() in the iterative estimation procedure, the estimate of the threshold
in the iterative estimation procedure, the estimate of the threshold ![]() is set to the upper bound and maximum likelihood estimates of
is set to the upper bound and maximum likelihood estimates of ![]() and
and ![]() are computed.
are computed.
INEST Data Set for the Three-Parameter Weibull
You can specify a SAS data set to set lower bounds, upper bounds, equality constraints, or initial values for estimating
the parameters of a three-parameter Weibull distribution by using the INEST= option in the ANALYZE or PROBPLOT statement.
The data set must contain a variable named _TYPE_ that specifies the action that you want to take in the iterative estimation process, and some combination of variables named
_SCALE_, _SHAPE_, and _THRESHOLD_ that represent the distribution parameters. If BY processing is used, the INEST= data set should also include the BY variables,
and there must be at least one observation for each BY group.
The possible values of _TYPE_ and corresponding actions are summarized in Table 16.66.
Table 16.66: _TYPE_ Variable Values
|
Value of |
Action |
|---|---|
|
LB |
Lower bound |
|
UB |
Upper bound |
|
EQ |
Equality |
|
PARMS |
Initial value |
For example, you can use the INEST data set In created by using the following SAS statements to specify bounds for data that contain the BY variable Group with three BY groups: A, B, and D. The data set In specifies a lower bound for the threshold parameter of –100 for groups A, B, and D, and an upper bound of 3 for the threshold
parameter for group D. Since the variables _Scale_ and _Shape_ are set to missing, no action is taken for them, and these variables could be omitted from the data set.
data In; input Group$1 _Type_$ 2-11 _Scale_ _Shape_ _Threshold_; datalines; A lb . . -100 B lb . . -100 D lb . . -100 D ub . . 3 ;
Regression Models
You can specify a regression model by using the MODEL statement. For example, if you want to relate the lifetimes of electronic parts in a test to Arrhenius-transformed operating temperature, then an appropriate model might be
|
|
where ![]() , and
, and ![]() is the centigrade temperature at which the ith unit is tested. Here,
is the centigrade temperature at which the ith unit is tested. Here, ![]() [ 1
[ 1 ![]() ].
].
There are two types of explanatory variables: continuous variables and classification variables. Continuous variables represent physical quantities, such as temperature or voltage, and they must be numeric. Continuous explanatory variables are sometimes called covariates.
Classification variables identify classification levels and are declared in the CLASS statement. These are also referred to
as categorical, dummy, qualitative, discrete, or nominal variables. Classification variables can be either character or numeric. The values of classification variables are called
levels. For example, the classification variable Batch could have levels ‘batch1’ and ‘batch2’ to identify items from two production batches. An indicator (0-1) variable is generated
for each level of a classification variable and is used as an explanatory variable. See Nelson (1990, p. 277) for an example that uses an indicator variable in the analysis of accelerated life test data. In a model, an explanatory
variable that is not declared in a CLASS statement is assumed to be continuous.
By default, all regression models automatically contain an intercept term; that is, the model is of the form
|
|
where ![]() does not have an explanatory variable multiplier. The intercept term can be excluded from the model by specifying INTERCEPT=0
as a MODEL statement option.
does not have an explanatory variable multiplier. The intercept term can be excluded from the model by specifying INTERCEPT=0
as a MODEL statement option.
For numerical stability, continuous explanatory variables are centered and scaled internally to the procedure. This transforms
the parameters ![]() in the original model to a new set of parameters. The parameter estimates
in the original model to a new set of parameters. The parameter estimates ![]() and covariances are transformed back to the original scale before reporting, so that the parameters should be interpreted
in terms of the originally specified model. Covariates that are indicator variables—that is, those specified in a CLASS statement—are
not centered and scaled.
and covariances are transformed back to the original scale before reporting, so that the parameters should be interpreted
in terms of the originally specified model. Covariates that are indicator variables—that is, those specified in a CLASS statement—are
not centered and scaled.
Initial values of the regression parameters used in the Newton-Raphson method are computed by ordinary least squares. The
parameters ![]() and the scale parameter
and the scale parameter ![]() are jointly estimated by maximum likelihood, taking a logarithmic transformation of the responses, if necessary, to get a
location-scale model.
are jointly estimated by maximum likelihood, taking a logarithmic transformation of the responses, if necessary, to get a
location-scale model.
The generalized gamma distribution is fit using log lifetime as the response variable. The regression parameters ![]() , the scale parameter
, the scale parameter ![]() , and the shape parameter
, and the shape parameter ![]() are jointly estimated.
are jointly estimated.
The Weibull distribution shape parameter estimate is computed as ![]() , where
, where ![]() is the scale parameter from the corresponding extreme value distribution. The Weibull scale parameter
is the scale parameter from the corresponding extreme value distribution. The Weibull scale parameter ![]() is not computed by the procedure. Instead, the regression parameters
is not computed by the procedure. Instead, the regression parameters ![]() and the shape
and the shape ![]() are reported.
are reported.
In a model with one to three continuous explanatory variables x, you can use the RELATION= option in the MODEL statement to specify a transformation that is applied to the variables before model fitting. Table 16.67 shows the available transformations.
Table 16.67: Variable Transformations
|
Relation |
Transformed variable |
|---|---|
|
ARRHENIUS (Nelson parameterization) |
|
|
ARRHENIUS2 (activation energy parameterization) |
|
|
POWER |
|
|
LINEAR |
x |
|
LOGISTIC |
|
Nonconstant Scale Parameter
In some situations, it is desirable for the scale parameter to change with the values of explanatory variables. For example, Meeker and Escobar (1998, section 17.5) present an analysis of accelerated life test data where the spread of the data is greater at lower levels of the stress. You can use the LOGSCALE statement to specify the scale parameter as a function of explanatory variables. You must also have a MODEL statement to specify the location parameter. Explanatory variables can be continuous variables, indicator variables specified in the CLASS statement, or any interaction combination. The variables can be the same as specified in the MODEL statement, or they can be different variables. Any transformation specified with the RELATION= MODEL statement option will be applied to the same variable appearing in the LOGSCALE statement. See the section Regression Model with Nonconstant Scale for an example of fitting a model with nonconstant scale parameter.
The form of the model for the scale parameter is
|
|
where ![]() is the intercept term. The intercept term can be excluded from the model by specifying INTERCEPT=0 as a LOGSCALE statement
option.
is the intercept term. The intercept term can be excluded from the model by specifying INTERCEPT=0 as a LOGSCALE statement
option.
The parameters ![]() are estimated by maximum likelihood jointly with all the other parameters in the model.
are estimated by maximum likelihood jointly with all the other parameters in the model.
Stable Parameters
The location and scale parameters ![]() are estimated by maximizing the likelihood function by numerical methods, as described previously. An alternative parameterization
that is likely to have better numerical properties for heavy censoring is
are estimated by maximizing the likelihood function by numerical methods, as described previously. An alternative parameterization
that is likely to have better numerical properties for heavy censoring is ![]() , where
, where ![]() and
and ![]() is the pth quantile of the standardized distribution. See Meeker and Escobar (1998, p. 90) and Doganaksoy and Schmee (1993) for more details on alternate parameterizations.
is the pth quantile of the standardized distribution. See Meeker and Escobar (1998, p. 90) and Doganaksoy and Schmee (1993) for more details on alternate parameterizations.
By default, RELIABILITY estimates a value of ![]() from the data that will improve the numerical properties of the estimation. You can also specify values of p from which the value of
from the data that will improve the numerical properties of the estimation. You can also specify values of p from which the value of ![]() will be computed with the PSTABLE= option in the ANALYZE, PROBPLOT, RELATIONPLOT, or MODEL statement. Note that a value of
p = 0.632 for the Weibull and extreme value and p = 0.5 for all other distributions will give
will be computed with the PSTABLE= option in the ANALYZE, PROBPLOT, RELATIONPLOT, or MODEL statement. Note that a value of
p = 0.632 for the Weibull and extreme value and p = 0.5 for all other distributions will give ![]() and the parameterization will then be the usual location-scale parameterization.
and the parameterization will then be the usual location-scale parameterization.
All estimates and related statistics are reported in terms of the location and scale parameters ![]() . If you specify the ITPRINT option in the ANALYZE, PROBPLOT, or RELATIONPLOT statement, a table showing the values of p,
. If you specify the ITPRINT option in the ANALYZE, PROBPLOT, or RELATIONPLOT statement, a table showing the values of p, ![]() ,
, ![]() , and the last evaluation of the gradient and Hessian for these parameters is produced.
, and the last evaluation of the gradient and Hessian for these parameters is produced.
Covariance Matrix
An estimate of the covariance matrix of the maximum likelihood estimators (MLEs) of the parameters ![]() is given by the inverse of the negative of the matrix of second derivatives of the log likelihood, evaluated at the final
parameter estimates:
is given by the inverse of the negative of the matrix of second derivatives of the log likelihood, evaluated at the final
parameter estimates:
|
|
The negative of the matrix of second derivatives is called the observed Fisher information matrix. The diagonal term ![]() is an estimate of the variance of
is an estimate of the variance of ![]() . Estimates of standard errors of the MLEs are provided by
. Estimates of standard errors of the MLEs are provided by
|
|
An estimator of the correlation matrix is
|
|
The covariance matrix for the Weibull distribution parameter estimators is computed by a first-order approximation from the
covariance matrix of the estimators of the corresponding extreme value parameters ![]() as
as
|
|
|
|
|
|
|
|
|
|
|
|
For the regression model, the variance of the Weibull shape parameter estimator ![]() is computed from the variance of the estimator of the extreme value scale parameter
is computed from the variance of the estimator of the extreme value scale parameter ![]() as shown previously. The covariance of the regression parameter estimator
as shown previously. The covariance of the regression parameter estimator ![]() and the Weibull shape parameter estimator
and the Weibull shape parameter estimator ![]() is computed in terms of the covariance between
is computed in terms of the covariance between ![]() and
and ![]() as
as
|
|
Confidence Intervals for Distribution Parameters
Table 16.68 shows the method of computation of approximate two-sided ![]() confidence limits for distribution parameters. The default value of confidence is
confidence limits for distribution parameters. The default value of confidence is ![]() . Other values of confidence are specified using the CONFIDENCE= option. In Table 16.68,
. Other values of confidence are specified using the CONFIDENCE= option. In Table 16.68, ![]() represents the
represents the ![]() percentile of the standard normal distribution, and
percentile of the standard normal distribution, and ![]() and
and ![]() are the MLEs of the location and scale parameters for the normal, extreme value, and logistic distributions. For the lognormal,
Weibull, and log-logistic distributions,
are the MLEs of the location and scale parameters for the normal, extreme value, and logistic distributions. For the lognormal,
Weibull, and log-logistic distributions, ![]() and
and ![]() represent the MLEs of the corresponding location and scale parameters of the location-scale distribution that results when
the logarithm of the lifetime is used as the response. For the Weibull distribution,
represent the MLEs of the corresponding location and scale parameters of the location-scale distribution that results when
the logarithm of the lifetime is used as the response. For the Weibull distribution, ![]() and
and ![]() are the location and scale parameters of the extreme value distribution for the logarithm of the lifetime.
are the location and scale parameters of the extreme value distribution for the logarithm of the lifetime. ![]() denotes the standard error of the MLE of
denotes the standard error of the MLE of ![]() , computed as the square root of the appropriate diagonal element of the inverse of the Fisher information matrix.
, computed as the square root of the appropriate diagonal element of the inverse of the Fisher information matrix.
Table 16.68: Confidence Limit Computation
|
Parameters |
|||
|---|---|---|---|
|
Distribution |
Location |
Scale |
Shape |
|
Threshold |
|||
|
Normal |
|
|
|
|
|
|
||
|
Lognormal |
|
|
|
|
|
|
||
|
Lognormal |
|
|
|
|
(base 10) |
|
|
|
|
Extreme value |
|
|
|
|
|
|
||
|
Weibull |
|
|
|
|
|
|
||
|
Exponential |
|
|
|
|
|
|
||
|
Logistic |
|
|
|
|
|
|
||
|
Log-logistic |
|
|
|
|
|
|
||
|
Generalized |
|
|
|
|
Gamma |
|
|
|
|
Three-parameter |
|
|
|
|
Weibull |
|
|
|
Regression Parameters
Approximate ![]() confidence limits for the regression parameter
confidence limits for the regression parameter ![]() are given by
are given by
|
|
|
|
Percentiles
The maximum likelihood estimate of the ![]() percentile
percentile ![]() for the extreme value, normal, and logistic distributions is given by
for the extreme value, normal, and logistic distributions is given by
|
|
where ![]() , G is the standardized CDF shown in Table 16.69, and
, G is the standardized CDF shown in Table 16.69, and ![]() are the maximum likelihood estimates of the location and scale parameters of the distribution. The maximum likelihood estimate
of the percentile
are the maximum likelihood estimates of the location and scale parameters of the distribution. The maximum likelihood estimate
of the percentile ![]() for the Weibull, lognormal, and log-logistic distributions is given by
for the Weibull, lognormal, and log-logistic distributions is given by
|
|
where ![]() , and G is the standardized CDF of the location-scale model corresponding to the logarithm of the response. For the lognormal (base
10) distribution,
, and G is the standardized CDF of the location-scale model corresponding to the logarithm of the response. For the lognormal (base
10) distribution,
|
|
The maximum likelihood estimate of the percentile ![]() for the three-parameter Weibull distribution is computed by
for the three-parameter Weibull distribution is computed by
|
|
where ![]() , and G is the standardized CDF of extreme value distribution.
, and G is the standardized CDF of extreme value distribution.
Table 16.69: Standardized Cumulative Distribution Functions
|
Location-Scale |
Location-Scale |
|
|---|---|---|
|
Distribution |
Distribution |
CDF |
|
Weibull |
Extreme value |
|
|
Lognormal |
Normal |
|
|
Log-logistic |
Logistic |
|
Confidence Intervals
The variance of the MLE of the ![]() percentile for the normal, extreme value, or logistic distribution is
percentile for the normal, extreme value, or logistic distribution is
|
|
Two-sided approximate ![]() confidence limits for
confidence limits for ![]() are
are
|
|
|
|
|
|
|
|
where ![]() represents the
represents the ![]() percentile of the standard normal distribution.
percentile of the standard normal distribution.
The limits for the lognormal, Weibull, or log-logistic distributions are
|
|
|
|
|
|
|
|
where ![]() refers to the percentile of the corresponding location-scale distribution (normal, extreme value, or logistic) for the logarithm
of the lifetime. For the lognormal (base 10) distribution,
refers to the percentile of the corresponding location-scale distribution (normal, extreme value, or logistic) for the logarithm
of the lifetime. For the lognormal (base 10) distribution,
|
|
|
|
|
|
|
|
Approximate limits for the three-parameter Weibull distribution are computed as
|
|
|
|
|
|
|
|
where ![]() refers to the percentile of the standard extreme value distribution.
refers to the percentile of the standard extreme value distribution.
Reliability Function
For the extreme value, normal, and logistic distributions shown in Table 16.69, the maximum likelihood estimate of the reliability function ![]() is given by
is given by
|
|
The MLE of the CDF is ![]() .
.
Confidence Intervals
Let ![]() . The approximate variance of u is
. The approximate variance of u is
|
|
Two-sided approximate ![]() confidence intervals for
confidence intervals for ![]() are computed as
are computed as
|
|
|
|
where
|
|
|
|
and ![]() represents the
represents the ![]() percentile of the standard normal distribution. The corresponding limits for the CDF are
percentile of the standard normal distribution. The corresponding limits for the CDF are
|
|
|
|
As an alternative, you can request that two-sided ![]() likelihood ratio confidence limits for the reliability function and the CDF be computed by specifying the LRCLSURV option in the ANALYZE statement or the LRCLSURV option in the PROBPLOT statement.
likelihood ratio confidence limits for the reliability function and the CDF be computed by specifying the LRCLSURV option in the ANALYZE statement or the LRCLSURV option in the PROBPLOT statement.
Limits for the Weibull, lognormal, and log-logistic reliability function ![]() are the same as those for the corresponding extreme value, normal, or logistic reliability
are the same as those for the corresponding extreme value, normal, or logistic reliability ![]() , where
, where ![]() . Limits for the three-parameter Weibull use
. Limits for the three-parameter Weibull use ![]() and the extreme value CDF.
and the extreme value CDF.
You can create a table containing estimates of the reliability function, the CDF, and confidence limits computed as described in this section with the SURVTIME= option in the ANALYZE statement or with the SURVTIME= option in the PROBPLOT statement. You can plot confidence limits for the CDF on probability plots created with the PROBPLOT statement with the PINTERVALS=CDF option in the PROBPLOT statement. PINTERVALS=CDF is the default option for parametric confidence limits on probability plots.
Estimation with the Binomial and Poisson Distributions
In addition to estimating the parameters of the distributions in Table 16.57, you can estimate parameters, compute confidence limits, compute predicted values and prediction limits, and compute chi-square tests for differences in groups for the binomial and Poisson distributions by using the ANALYZE statement. Specify either BINOMIAL or POISSON in the DISTRIBUTION statement to use one of these distributions. The ANALYZE statement options available for the binomial and Poisson distributions are given in Table 16.5. See the section Analysis of Binomial Data for an example of an analysis of binomial data.
Binomial Distribution
If r is the number of successes and n is the number of trials in a binomial experiment, then the maximum likelihood estimator of the probability p in the binomial distribution in Table 16.59 is computed as
|
|
Two-sided ![]() confidence limits for p are computed as in Johnson, Kotz, and Kemp (1992, p. 130):
confidence limits for p are computed as in Johnson, Kotz, and Kemp (1992, p. 130):
|
|
with ![]() and
and ![]() and
and
|
|
with ![]() and
and ![]() , where
, where ![]() is the
is the ![]() percentile of the F distribution with
percentile of the F distribution with ![]() degrees of freedom in the numerator and
degrees of freedom in the numerator and ![]() degrees of freedom in the denominator.
degrees of freedom in the denominator.
You can compute a sample size required to estimate p within a specified tolerance w with probability ![]() . Nelson (1982, p. 206) gives the following formula for the approximate sample size:
. Nelson (1982, p. 206) gives the following formula for the approximate sample size:
|
|
where ![]() is the
is the ![]() percentile of the standard normal distribution. The formula is based on the normal approximation for the distribution of
percentile of the standard normal distribution. The formula is based on the normal approximation for the distribution of
![]() . Nelson recommends using this formula if
. Nelson recommends using this formula if ![]() and
and ![]() . The value of
. The value of ![]() used for computing confidence limits is used in the sample size computation. The default value of confidence is
used for computing confidence limits is used in the sample size computation. The default value of confidence is ![]() . Other values of confidence are specified using the CONFIDENCE= option. You specify a tolerance of number with the TOLERANCE(number) option.
. Other values of confidence are specified using the CONFIDENCE= option. You specify a tolerance of number with the TOLERANCE(number) option.
The predicted number of successes X in a future sample of size m, based on the previous estimate of p, is computed as
|
|
Two-sided approximate ![]() prediction limits are computed as in Nelson (1982, p. 208). The prediction limits are the solutions
prediction limits are computed as in Nelson (1982, p. 208). The prediction limits are the solutions ![]() and
and ![]() of
of
|
|
|
|
where ![]() is the
is the ![]() % percentile of the F distribution with
% percentile of the F distribution with ![]() degrees of freedom in the numerator and
degrees of freedom in the numerator and ![]() degrees of freedom in the denominator. You request predicted values and prediction limits for a future sample of size number with the PREDICT(number) option.
degrees of freedom in the denominator. You request predicted values and prediction limits for a future sample of size number with the PREDICT(number) option.
You can test groups of binomial data for equality of their binomial probability by using the ANALYZE statement. You specify the K groups to be compared with a group variable having K levels.
Nelson (1982, p. 450) discusses a chi-square test statistic for comparing K binomial proportions for equality. Suppose there are ![]() successes in
successes in ![]() trials for
trials for ![]() . The grouped estimate of the binomial probability is
. The grouped estimate of the binomial probability is
|
|
The chi-square test statistic for testing the hypothesis ![]() against
against ![]() for some i and j is
for some i and j is
|
|
The statistic Q has an asymptotic chi-square distribution with K – 1 degrees of freedom. The RELIABILITY procedure computes the contribution of each group to Q, the value of Q, and the p-value for Q based on the limiting chi-square distribution with K – 1 degrees of freedom. If you specify the PREDICT option, predicted values and prediction limits are computed for each group,
as well as for the pooled group. The p-value is defined as ![]() , where
, where ![]() is the chi-square CDF with K – 1 degrees of freedom, and Q is the observed value. A test of the hypothesis of equal binomial probabilities among the groups with significance level
is the chi-square CDF with K – 1 degrees of freedom, and Q is the observed value. A test of the hypothesis of equal binomial probabilities among the groups with significance level
![]() is
is
-
 : do not reject the equality hypothesis
: do not reject the equality hypothesis
-
 : reject the equality hypothesis
: reject the equality hypothesis
Poisson Distribution
You can use the ANALYZE statement to model data by using the Poisson distribution. The data consist of a count Y of occurrences in a “length” of observation T. Observation T is typically an exposure time, but it can have other units, such as distance. The ANALYZE statement enables you to compute the rate of occurrences, confidence limits, and prediction limits.
An estimate of the rate ![]() is computed as
is computed as
|
|
Two-sided ![]() confidence limits for
confidence limits for ![]() are computed as in Nelson (1982, p. 201):
are computed as in Nelson (1982, p. 201):
|
|
|
|
where ![]() is the
is the ![]() percentile of the chi-square distribution with
percentile of the chi-square distribution with ![]() degrees of freedom.
degrees of freedom.
You can compute a length T required to estimate ![]() within a specified tolerance w with probability
within a specified tolerance w with probability ![]() . Nelson (1982, p. 202) provides the following approximate formula:
. Nelson (1982, p. 202) provides the following approximate formula:
|
|
where ![]() is the
is the ![]() percentile of the standard normal distribution. The formula is based on the normal approximation for
percentile of the standard normal distribution. The formula is based on the normal approximation for ![]() and is more accurate for larger values of
and is more accurate for larger values of ![]() . Nelson recommends using the formula when
. Nelson recommends using the formula when ![]() . The value of
. The value of ![]() used for computing confidence limits is also used in the length computation. The default value of confidence is
used for computing confidence limits is also used in the length computation. The default value of confidence is ![]() . Other values of confidence are specified using the CONFIDENCE= option. You specify a tolerance of number with the TOLERANCE(number) option.
. Other values of confidence are specified using the CONFIDENCE= option. You specify a tolerance of number with the TOLERANCE(number) option.
The predicted future number of occurrences in a length S is
|
|
Two-sided approximate ![]() prediction limits are computed as in Nelson (1982, p. 203). The prediction limits are the solutions
prediction limits are computed as in Nelson (1982, p. 203). The prediction limits are the solutions ![]() and
and ![]() of
of
|
|
|
|
where ![]() is the
is the ![]() percentile of the F distribution with
percentile of the F distribution with ![]() degrees of freedom in the numerator and
degrees of freedom in the numerator and ![]() degrees of freedom in the denominator. You request predicted values and prediction limits for a future exposure number with the PREDICT(number) option.
degrees of freedom in the denominator. You request predicted values and prediction limits for a future exposure number with the PREDICT(number) option.
You can compute a chi-square test statistic for comparing K Poisson rates for equality. You specify the K groups to be compared with a group variable having K levels.
See Nelson (1982, p. 444) for more information. Suppose that there are ![]() Poisson counts in lengths
Poisson counts in lengths ![]() for
for ![]() and that the
and that the ![]() are independent. The grouped estimate of the Poisson rate is
are independent. The grouped estimate of the Poisson rate is
|
|
The chi-square test statistic for testing the hypothesis ![]() against
against ![]() for some i and j is
for some i and j is
|
|
The statistic Q has an asymptotic chi-square distribution with K – 1 degrees of freedom. The RELIABILITY procedure computes the contribution of each group to Q, the value of Q, and the p-value for Q based on the limiting chi-square distribution with K – 1 degrees of freedom. If you specify the PREDICT option, predicted values and prediction limits are computed for each group,
as well as for the pooled group. The p-value is defined as ![]() , where
, where ![]() is the chi-square CDF with K – 1 degrees of freedom and Q is the observed value. A test of the hypothesis of equal Poisson rates among the groups with significance level
is the chi-square CDF with K – 1 degrees of freedom and Q is the observed value. A test of the hypothesis of equal Poisson rates among the groups with significance level ![]() is
is
-
 : accept the equality hypothesis
: accept the equality hypothesis
-
 : reject the equality hypothesis
: reject the equality hypothesis
Least Squares Fit to the Probability Plot
Fitting to the probability plot by least squares is an alternative to maximum likelihood estimation of the parameters of a
life distribution. Only the failure times are used. A least squares fit is computed using points ![]() , where
, where ![]() and
and ![]() are the plotting positions as defined in the section Probability Plotting. The
are the plotting positions as defined in the section Probability Plotting. The ![]() are either the lifetimes for the normal, extreme value, or logistic distributions or the log lifetimes for the lognormal,
Weibull, or log-logistic distributions. The ANALYZE, PROBPLOT, or RELATIONPLOT statement option FITTYPE=LSXY specifies the
are either the lifetimes for the normal, extreme value, or logistic distributions or the log lifetimes for the lognormal,
Weibull, or log-logistic distributions. The ANALYZE, PROBPLOT, or RELATIONPLOT statement option FITTYPE=LSXY specifies the
![]() as the dependent variable (’y-coordinate’) and the
as the dependent variable (’y-coordinate’) and the ![]() as the independent variable (’x-coordinate’). You can optionally reverse the quantities used as dependent and independent
variables by specifying the FITTYPE=LSYX option.
as the independent variable (’x-coordinate’). You can optionally reverse the quantities used as dependent and independent
variables by specifying the FITTYPE=LSYX option.
Weibayes Estimation
Weibayes estimation is a method of performing a Weibull analysis when there are few or no failures. The FITTYPE=WEIBAYES option
requests this method. The method of Nelson (1985) is used to compute a one-sided confidence interval for the Weibull scale parameter when the Weibull shape parameter is specified.
See Abernethy (2006) for more discussion and examples. The Weibull shape parameter ![]() is assumed to be known and is specified to the procedure with the SHAPE=number option. Let
is assumed to be known and is specified to the procedure with the SHAPE=number option. Let ![]() be the failure and censoring times, and let
be the failure and censoring times, and let ![]() be the number of failures in the data. If there are no failures
be the number of failures in the data. If there are no failures ![]() , a lower
, a lower ![]() confidence limit for the Weibull scale parameter
confidence limit for the Weibull scale parameter ![]() is computed as
is computed as
|
|
The default value of confidence is ![]() . Other values of confidence are specified using the CONFIDENCE= option.
. Other values of confidence are specified using the CONFIDENCE= option.
If ![]() , the MLE of
, the MLE of ![]() is given by
is given by
|
|
and a lower ![]() confidence limit for the Weibull scale parameter
confidence limit for the Weibull scale parameter ![]() is computed as
is computed as
|
|
where ![]() is the
is the ![]() percentile of a chi-square distribution with
percentile of a chi-square distribution with ![]() degrees of freedom. The procedure uses the specified value of
degrees of freedom. The procedure uses the specified value of ![]() and the computed value of
and the computed value of ![]() to compute distribution percentiles and the reliability function.
to compute distribution percentiles and the reliability function.
Estimation With Multiple Failure Modes
In many applications, units can experience multiple causes of failure, or failure modes. For example, in the section Weibull Probability Plot for Two Combined Failure Modes, insulation specimens can experience either early failures due to manufacturing defects or degradation failures due to aging. The FMODE statement is used to analyze this type of data. See the section FMODE Statement for the syntax of the FMODE statement. This section describes the analysis of data when units experience multiple failure modes.
The assumptions used in the analysis are
-
a cause, or mode, can be identified for each failure
-
failure modes follow a series-system model; i.e., a unit fails when a failure due to one of the modes occurs
-
each failure mode has the specified lifetime distribution with different parameters
-
failure modes act statistically independently
Suppose there are m failure modes, with lifetime distribution functions ![]() .
.
If you wish to estimate the lifetime distribution of a failure mode, say mode i, acting alone, specify the KEEP keyword in the FMODE statement. The failures from all other modes are treated as right-censored observations, and the lifetime distribution is estimated by one of the methods described in other sections, such as maximum likelihood. This lifetime distribution is interpreted as the distribution if the specified failure mode is acting alone, with all other modes eliminated. You can also specify more than one mode to KEEP, but the assumption is that all the specified modes have the same distribution.
If you specify the ELIMINATE keyword, failures due to the specified modes are treated as right censored. The resulting distribution estimate is the failure distribution if the specified modes are eliminated.
If you specify the COMBINE keyword, the failure distribution when all the modes specified in the FMODE statement modes act
is estimated. The failure distribution ![]() , from each individual mode is first estimated by treating all failures from other modes as right censored. The estimated
failure distributions are then combined to get an estimate of the lifetime distribution when all modes act,
, from each individual mode is first estimated by treating all failures from other modes as right censored. The estimated
failure distributions are then combined to get an estimate of the lifetime distribution when all modes act,
|
|
Pointwise approximate asymptotic normal confidence limits for ![]() can be obtained by the delta method. See Meeker and Escobar (1998, appendix B.2). The delta method variance of
can be obtained by the delta method. See Meeker and Escobar (1998, appendix B.2). The delta method variance of ![]() is, assuming independence of failure modes,
is, assuming independence of failure modes,
|
|
where ![]() , y is t for the extreme value, normal, and logistic distributions or
, y is t for the extreme value, normal, and logistic distributions or ![]() for the Weibull, lognormal or log-logistic distributions,
for the Weibull, lognormal or log-logistic distributions, ![]() and
and ![]() are location and scale parameter estimates for mode i, and
are location and scale parameter estimates for mode i, and ![]() and
and ![]() are the standard (
are the standard (![]() ) survival function and density function for the specified distribution.
) survival function and density function for the specified distribution.
Two-sided approximate ![]() pointwise confidence intervals are computed as in Meeker and Escobar (1998, section 3.6) as
pointwise confidence intervals are computed as in Meeker and Escobar (1998, section 3.6) as
|
|
where
|
|
where ![]() and
and ![]() is the pth quantile of the standard normal distribution.
is the pth quantile of the standard normal distribution.