The MVPMONITOR Procedure
Computing 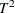 Control Limits
Control Limits
The control limits for the ![]() chart are the same for all the
chart are the same for all the ![]() statistics in the chart. The control limits are computed using the method of Tracy, Young, and Mason (1992), in which the distribution of the
statistics in the chart. The control limits are computed using the method of Tracy, Young, and Mason (1992), in which the distribution of the ![]() statistic is shown to follow a scaled beta distribution:
statistic is shown to follow a scaled beta distribution:
|
|
where i is the observation, j is the number of principal components in the model, and n is the number of observations used to build the principal component model.
The upper control limit is computed as the ![]() quantile of this distribution, and the lower control limit is computed by the
quantile of this distribution, and the lower control limit is computed by the ![]() quantile. You can use the ALPHA= option in the TSQUARECHART statement to specify
quantile. You can use the ALPHA= option in the TSQUARECHART statement to specify ![]() .
.
See the section Computing the ![]() and SPE Statistics for details of computing the
and SPE Statistics for details of computing the ![]() statistic based on a principal component model.
statistic based on a principal component model.
