The MVPMONITOR Procedure
Overview: MVPMONITOR Procedure
The MVPMONITOR procedure is used in conjunction with the MVPMODEL and MVPDIAGNOSE procedures to monitor multivariate process variation over time, to determine whether the process is stable, and to detect and diagnose changes in a stable process. Collectively, these three procedures are referred to as the MVP procedures. See Chapter 10: Introduction to Multivariate Process Monitoring Procedures, for a description of how the MVP procedures work together, and Chapter 12: The MVPMODEL Procedure, and Chapter 11: The MVPDIAGNOSE Procedure, for detailed descriptions of the other MVP procedures.
The MVPMONITOR procedure produces control charts for multivariate process data. It reads data sets that contain statistics
and principal component model information such as those created by the MVPMODEL procedure. The MVPMONITOR procedure creates
two types of multivariate control chart: 
charts and squared prediction error (SPE) charts. It can also produce contribution plots for out-of-control points in the
control charts.
Multivariate control charts detect unusual variation that would not be uncovered by individually monitoring the process variables with univariate control charts, such as Shewhart charts. A major impetus in the development of multivariate control charts is the inadequacy of individual univariate control charts in handling correlated measurement variables. A multivariate control chart can detect changes in the linear relationships of the variables in addition to their marginal means and variances.
The multivariate control charts that the MVPMONITOR procedure produces are based on principal component models that reduce
the dimensionality of the data by projecting the process measurements to a low-dimensional subspace that is defined by a small
number of principal components. This subspace is also known as the model hyperplane. charts are used to monitor variation within the model hyperplane, whereas SPE charts show variation from the model hyperplane.
The principal component approach offers several advantages over the construction of the classical chart:
-
It avoids computational issues that arise when the process variables are collinear and their covariance matrix is nearly singular.
-
It offers diagnostic tools for interpreting unusual values of
.
-
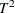By projecting the data to a low-dimensional subspace, it more adequately describes the variation in a multivariate process, which is often driven by a small number of underlying factors that are not directly observable.