Example 13.4 Creating a Classical 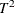Chart :: SAS/QC(R) 12.1 User's Guide

Example 13.4 Creating a Classical Chart

The following statements use PROC MVPMODEL to create a model from which classical charts can be produced:

proc mvpmodel data=flightDelays ncomp=all noprint out=mvpout;
   var AA CO DL F9 FL NW UA US WN;
run;

The NCOMP=ALL option specifies that the number of principal components equal the number of process variables, so the mvpout data set contains the classical statistic for each observation. The mvpout data set contains six observations per time point—one for each region.

The following statements create the classical chart:

proc mvpmonitor history=mvpout;
   time flightDate;
   series region;
   tsquarechart / seriesvalue='NE';
run;

The SERIES statement specifies region as the variable that identifies sequences of statistics, and the SERIESVALUE= option selects the region to be plotted, the Northeast. The classical chart is shown in Output 13.4.1.

Output 13.4.1: Classical Chart

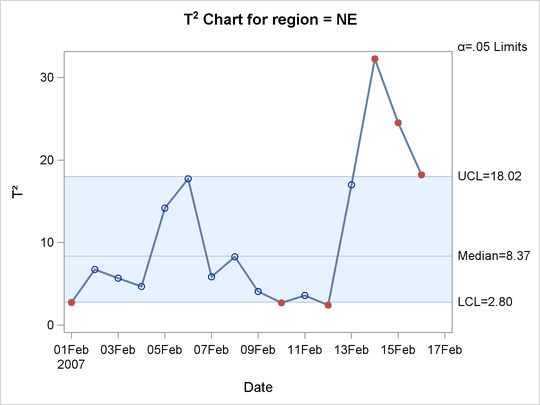
In this case, the classical chart finds out-of-control observations above the upper control limit during February 14–16 and below the lower control limit on February 1, 10, and 12.

Output 13.4.2 shows a partial listing of the mvpout data set. It contains statistics based on the model that has nine principal components, in addition to the original variables and other observationwise statistics.

Output 13.4.2: Partial Listing of Output Data Set mvpout

flightDate	region	AA	CO	DL	F9	FL	NW	UA	US	WN	Prin1	Prin2	Prin3	Prin4	Prin5	Prin6	Prin7	Prin8	Prin9	_NOBS_	_TSQUARE_	_SPE_
02/01/07	MW	14.9	7.1	7.9	8.5	14.8	4.5	5.1	13.4	5.1	-1.16440	0.89425	0.00118	-0.84496	0.07443	-0.05231	-0.27403	0.31880	-0.06726	96	3.2122	.
02/01/07	NE	15.7	7.1	8.6	6.3	14.6	6.2	7.0	11.0	6.4	-1.08197	0.55936	0.05859	-0.84487	-0.02092	-0.16851	-0.30596	0.25090	0.12804	96	2.7349	.
02/01/07	NW	17.8	2.6	6.1	28.8	11.6	6.1	11.6	27.3	3.7	-0.31223	2.23593	-0.03824	0.58893	0.21628	0.67149	0.85708	1.07348	-0.49530	96	18.5555	.
02/01/07	SC	19.9	8.3	13.9	4.9	25.8	15.3	9.0	15.1	12.8	0.22974	-0.16976	0.56118	-1.30139	0.22990	-0.34406	0.11471	0.30201	0.46481	96	6.3335	.
02/01/07	SE	16.1	1.9	8.7	8.7	15.1	18.3	4.0	10.4	6.5	-0.87056	0.01044	1.06975	-0.50179	0.38041	-0.33789	0.63114	0.45028	0.21437	96	6.1537	.

Notice that no SPE statistics are produced when the number of principal components equals the number of process variables.

The MVPMONITOR Procedure

Example 13.4 Creating a Classical Chart