The MVPMODEL Procedure
Relationship of Principal Components to Multivariate Control Charts
Multivariate control charts typically plot the ![]() statistic, which is a summary of multivariate variation. The classical
statistic, which is a summary of multivariate variation. The classical ![]() statistic is defined in Classical
statistic is defined in Classical ![]() Charts. When there is high correlation among the process variables, the correlation matrix is nearly singular. The subspace in which
the process varies can be adequately explained by fewer variables than the original p variables. Thus, the principal component approach to multivariate control charts is to project the original p variables into a lower-dimensional subspace by using a model based on j principal components, where
Charts. When there is high correlation among the process variables, the correlation matrix is nearly singular. The subspace in which
the process varies can be adequately explained by fewer variables than the original p variables. Thus, the principal component approach to multivariate control charts is to project the original p variables into a lower-dimensional subspace by using a model based on j principal components, where ![]() .
.
The key to the relationship between principal components and multivariate control charts is the decomposition of the sample
covariance matrix, ![]() , into the form
, into the form ![]() , where
, where ![]() is a diagonal matrix (Jackson, 1991; Mardia, Kent, and Bibby, 1979). This is also the eigenvalue decomposition of
is a diagonal matrix (Jackson, 1991; Mardia, Kent, and Bibby, 1979). This is also the eigenvalue decomposition of ![]() , where the columns of
, where the columns of ![]() are the eigenvectors and the diagonal elements of
are the eigenvectors and the diagonal elements of ![]() are the eigenvalues.
are the eigenvalues.
Equivalence of 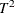 Statistics
Statistics
The ![]() statistic that is produced by the full principal component model is equivalent to the classical
statistic that is produced by the full principal component model is equivalent to the classical ![]() statistic. This is seen in the matrix representation of the
statistic. This is seen in the matrix representation of the ![]() statistic computed from a principal component model that uses all p components,
statistic computed from a principal component model that uses all p components,
|
|
Because ![]() is the zero matrix by construction, then
is the zero matrix by construction, then
|
|
Because ![]() , then
, then
![\[ \begin{array}{rl} T^2_ i & = \mb {t}_ i^{\prime } \mb {L}^{-1}_ n \mb {t}_ i \\ & = \left( \bP ^{\prime } \left( \mb {x_ i}- \bar{ \mb {x} } \right) \right)^{\prime } \mb {L}^{-1}_ n \left( \bP ^{\prime } \left( \mb {x_ i}- \bar{\mb {x} } \right) \right) \\ & = \left( \mb {x}_ i- \bar{ \mb {x} } \right)^{\prime } \mb {P} \mb {L}^{-1}_ n \mb {P}^{\prime } \left( \mb {x}_ i - \bar{ \mb {x} } \right) \\ & = \left( \mb {x}_ i- \bar{ \mb {x} } \right)^{\prime } \bS ^{-1} \left( \mb {x}_ i- \bar{ \mb {x} } \right) \end{array} \]](images/qcug_mvpmodel0038.png) |
which is the classical form. Consequently the classical ![]() statistic can be expressed as a sum of squares,
statistic can be expressed as a sum of squares,
|
|
where ![]() is the variance of the kth principal component.
is the variance of the kth principal component.
Computing the 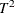 and SPE Statistics
and SPE Statistics
Creating a ![]() chart that is based on a principal component model begins with choosing the number (j) of principal components. Effectively, this involves selecting a subspace in
chart that is based on a principal component model begins with choosing the number (j) of principal components. Effectively, this involves selecting a subspace in ![]() dimensions and then creating a
dimensions and then creating a ![]() statistic based on that j-component model.
statistic based on that j-component model.
The ![]() statistic is meant to monitor variation in the model space. However, if variation appears in the
statistic is meant to monitor variation in the model space. However, if variation appears in the ![]() subspace orthogonal to model space, then the model assumptions and physical process should be reexamined. Variation outside
the model space can be detected with an SPE chart.
subspace orthogonal to model space, then the model assumptions and physical process should be reexamined. Variation outside
the model space can be detected with an SPE chart.
In a model with j principal components, the ![]() statistic is calculated as
statistic is calculated as
|
|
where ![]() is the principal component score for the kth principal component of the ith observation and
is the principal component score for the kth principal component of the ith observation and ![]() is the standard deviation of
is the standard deviation of ![]() .
.
The information in the remaining ![]() principal components is monitored with charts for the SPE statistic, which is calculated as
principal components is monitored with charts for the SPE statistic, which is calculated as
|
|
