The MVPMODEL Procedure
Classical 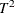 Charts
Charts
Classical ![]() charts are defined as follows. Assume that there are n observations for p variables, denoted by
charts are defined as follows. Assume that there are n observations for p variables, denoted by ![]() , where
, where ![]() is a p-dimensional vector. The
is a p-dimensional vector. The ![]() statistic for observation i is
statistic for observation i is
|
|
where
![\[ \begin{array}{lcr} \bar{X}_ j = \frac{1}{n} \sum _{i=1}^ n X_{ij}~ ~ , & \mb {X}_ i = \left[ \begin{array}{c} X_{i1} \\ X_{i2} \\ \vdots \\ X_{ip} \end{array} \right] , & \bar{\mb {X}}_ n = \left[ \begin{array}{c} \bar{X}_{1} \\ \bar{X}_{2} \\ \vdots \\ \bar{X}_{p} \end{array} \right] \end{array} \]](images/qcug_mvpmodel0011.png) |
and
|
|
For purposes of deriving control limits for the ![]() chart, it is assumed that
chart, it is assumed that ![]() has a p-dimensional multivariate normal distribution with mean vector
has a p-dimensional multivariate normal distribution with mean vector ![]() and covariance matrix
and covariance matrix ![]() for
for ![]() . The classical formulation of the
. The classical formulation of the ![]() chart does not involve a principal component model for the data, and it bases the computation of
chart does not involve a principal component model for the data, and it bases the computation of ![]() on the sample covariance matrix
on the sample covariance matrix ![]() . See Alt (1985) for theoretical details and the section Multivariate Control Charts for an example.
. See Alt (1985) for theoretical details and the section Multivariate Control Charts for an example.
A classical ![]() chart is equivalent to a
chart is equivalent to a ![]() chart based on a full principal component model (with p components), as discussed in the section Relationship of Principal Components to Multivariate Control Charts. See Example 12.2 for more information.
chart based on a full principal component model (with p components), as discussed in the section Relationship of Principal Components to Multivariate Control Charts. See Example 12.2 for more information.
