XCHART Statement: CUSUM Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Basic Notation for Cusum ChartsFormulas for Cumulative SumsDefining the Decision Interval for a One-Sided Cusum SchemeDefining the V-Mask for a Two-Sided Cusum SchemeDesigning a Cusum SchemeCusum Charts Compared with Shewhart ChartsMethods for Estimating the Standard DeviationOutput Data SetsODS TablesODS GraphicsInput Data SetsMissing Values
Basic Notation for Cusum ChartsFormulas for Cumulative SumsDefining the Decision Interval for a One-Sided Cusum SchemeDefining the V-Mask for a Two-Sided Cusum SchemeDesigning a Cusum SchemeCusum Charts Compared with Shewhart ChartsMethods for Estimating the Standard DeviationOutput Data SetsODS TablesODS GraphicsInput Data SetsMissing Values -
Examples

Example 6.1 Cusum and Standard Deviation Charts
See CUSXS in the SAS/QC Sample LibraryWhen you are working with subgrouped data, it can be helpful to accompany a cusum chart for means with a Shewhart s chart for monitoring the variability of the process. This example creates this combination for the variable Weight in the data set Oil (see Creating a V-Mask Cusum Chart from Raw Data).
The first step is to create a one-sided cusum chart for means that detects a shift of one standard error (![]() ) below the target mean.
) below the target mean.
proc cusum data=Oil;
xchart Weight*Hour /
nochart
mu0=8.100 /* target mean for process */
sigma0=0.050 /* known standard deviation */
delta=-1 /* shift to be detected */
h=3 /* cusum parameter h */
k=0.5 /* cusum parameter k */
scheme=onesided
outtable = Tabcusum
( drop = _var_ _subn_ _subx_ _exlim_
rename = ( _cusum_ = _subx_ _h_ = _uclx_ ) )
;
run;
The results are saved in an OUTTABLE= data set named Tabcusum. The cusum variable (_CUSUM_) and the decision interval variable (_H_) are renamed to _SUBX_ and _LCLX_ so that they can later be read by the SHEWHART procedure.
The next step is to construct a Shewhart ![]() and s chart for
and s chart for Weight and save the results in a data set named Tabxscht.
proc shewhart data=Oil;
xschart Weight*Hour /
nochart
outtable = Tabxscht
( drop = _subx_ _uclx_ );
run;
Note that the variables _SUBX_ and _UCLX_ are dropped from Tabxscht.
The third step is to merge the data sets Tabcusum and Tabxscht.
data taball; merge Tabxscht Tabcusum; by Hour; _mean_ = _uclx_ * 0.5; _lclx_ = 0.0; run;
The variable _LCLX_ is assigned the role of the lower limit for the cusums, and the variable _MEAN_ is assigned a dummy value. Now, TABALL, which is listed in Output 6.1.1, has the structure required for a TABLE= data set used with the XSCHART statement in the SHEWHART procedure (see TABLE= Data Set).
Output 6.1.1: Listing of the Data Set TABALL
| Obs | _VAR_ | Hour | _SIGMAS_ | _LIMITN_ | _SUBN_ | _LCLX_ | _MEAN_ | _STDDEV_ | _EXLIM_ | _LCLS_ | _SUBS_ | _S_ | _UCLS_ | _EXLIMS_ | _subx_ | _uclx_ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Weight | 1 | 3 | 4 | 4 | 0 | 1.5 | 0.05 | 0 | 0.059640 | 0.049943 | 0.11317 | 0.00 | 3 | ||
| 2 | Weight | 2 | 3 | 4 | 4 | 0 | 1.5 | 0.05 | 0 | 0.090220 | 0.049943 | 0.11317 | 0.00 | 3 | ||
| 3 | Weight | 3 | 3 | 4 | 4 | 0 | 1.5 | 0.05 | 0 | 0.076346 | 0.049943 | 0.11317 | 0.00 | 3 | ||
| 4 | Weight | 4 | 3 | 4 | 4 | 0 | 1.5 | 0.05 | 0 | 0.025552 | 0.049943 | 0.11317 | 0.00 | 3 | ||
| 5 | Weight | 5 | 3 | 4 | 4 | 0 | 1.5 | 0.05 | 0 | 0.026500 | 0.049943 | 0.11317 | 0.00 | 3 | ||
| 6 | Weight | 6 | 3 | 4 | 4 | 0 | 1.5 | 0.05 | 0 | 0.075617 | 0.049943 | 0.11317 | 0.30 | 3 | ||
| 7 | Weight | 7 | 3 | 4 | 4 | 0 | 1.5 | 0.05 | 0 | 0.037242 | 0.049943 | 0.11317 | 0.00 | 3 | ||
| 8 | Weight | 8 | 3 | 4 | 4 | 0 | 1.5 | 0.05 | 0 | 0.059290 | 0.049943 | 0.11317 | 0.18 | 3 | ||
| 9 | Weight | 9 | 3 | 4 | 4 | 0 | 1.5 | 0.05 | 0 | 0.005737 | 0.049943 | 0.11317 | 1.21 | 3 | ||
| 10 | Weight | 10 | 3 | 4 | 4 | 0 | 1.5 | 0.05 | 0 | 0.046522 | 0.049943 | 0.11317 | 0.62 | 3 | ||
| 11 | Weight | 11 | 3 | 4 | 4 | 0 | 1.5 | 0.05 | 0 | 0.040542 | 0.049943 | 0.11317 | 0.00 | 3 | ||
| 12 | Weight | 12 | 3 | 4 | 4 | 0 | 1.5 | 0.05 | 0 | 0.056103 | 0.049943 | 0.11317 | 0.00 | 3 |
The final step is to use the SHEWHART procedure to read TABALL as a TABLE= data set and to display the cusum and s charts.
ods graphics off;
symbol v=dot color=salmon h=1.8 pct;
title 'Cusum Chart for Mean and s chart';
proc shewhart table=taball;
xschart Weight * Hour /
nolimitslegend
ucllabel = 'h=3.0'
noctl
split = '/'
nolegend ;
label _subx_ = 'Lower Cusum/Std Dev';
run;
The central line for the primary (cusum) chart is suppressed with the NOCTL option, and the default 3![]() Limits legend is suppressed with the NOLIMITLEGEND option. The charts are shown in Output 6.1.2.
Limits legend is suppressed with the NOLIMITLEGEND option. The charts are shown in Output 6.1.2.
Output 6.1.2: Combined Cusum Chart and s Chart
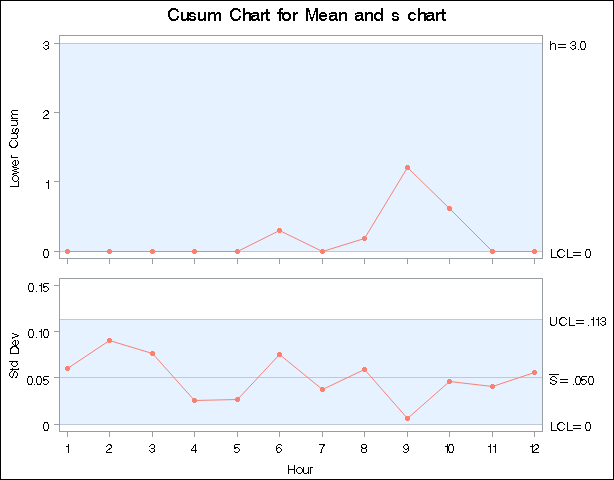
The process variability is stable, and there is no signal of a downward shift in the process mean.