XCHART Statement: CUSUM Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Basic Notation for Cusum ChartsFormulas for Cumulative SumsDefining the Decision Interval for a One-Sided Cusum SchemeDefining the V-Mask for a Two-Sided Cusum SchemeDesigning a Cusum SchemeCusum Charts Compared with Shewhart ChartsMethods for Estimating the Standard DeviationOutput Data SetsODS TablesODS GraphicsInput Data SetsMissing Values
Basic Notation for Cusum ChartsFormulas for Cumulative SumsDefining the Decision Interval for a One-Sided Cusum SchemeDefining the V-Mask for a Two-Sided Cusum SchemeDesigning a Cusum SchemeCusum Charts Compared with Shewhart ChartsMethods for Estimating the Standard DeviationOutput Data SetsODS TablesODS GraphicsInput Data SetsMissing Values -
Examples

Cusum Charts Compared with Shewhart Charts
Although cusum charts and Shewhart charts are both used to detect shifts in the process mean, there are important differences in the two methods.
-
Each point on a Shewhart chart is based on information for a single subgroup sample or measurement. Each point on a cusum chart is based on information from all samples (measurements) up to and including the current sample (measurement).
-
On a Shewhart chart, upper and lower control limits are used to decide whether a point signals an out-of-control condition. On a cusum chart, the limits take the form of a decision interval or a V-mask.
-
On a Shewhart chart, the control limits are commonly computed as 3
 limits. On a cusum chart, the limits are determined from average run length specifications, specified error probabilities,
or an economic design.
limits. On a cusum chart, the limits are determined from average run length specifications, specified error probabilities,
or an economic design.
A cusum chart offers several advantages over a Shewhart chart.
-
A cusum chart is more efficient for detecting small shifts in the process mean, in particular, shifts of 0.5 to 2 standard deviations from the target mean (refer to Montgomery 1996). Lucas (1976) noted that “a V-mask designed to detect a
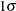 shift will detect it about four times as fast as a competing Shewhart chart.”
shift will detect it about four times as fast as a competing Shewhart chart.”
-
Shifts in the process mean are visually easy to detect on a cusum chart since they produce a change in the slope of the plotted points. The point at which the slope changes is the point at which the shift has occurred.
These advantages are not as pronounced if the Shewhart chart is augmented by the tests for special causes described by Nelson (1984, 1985). Also see Tests for Special Causes: SHEWHART Procedure. Moreover,
-
cusum schemes are more complicated to design.
-
a cusum chart can be slower to detect large shifts in the process mean.
-
it can be difficult to interpret point patterns on a cusum chart since the cusums are correlated.