XCHART Statement: CUSUM Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Basic Notation for Cusum ChartsFormulas for Cumulative SumsDefining the Decision Interval for a One-Sided Cusum SchemeDefining the V-Mask for a Two-Sided Cusum SchemeDesigning a Cusum SchemeCusum Charts Compared with Shewhart ChartsMethods for Estimating the Standard DeviationOutput Data SetsODS TablesODS GraphicsInput Data SetsMissing Values
Basic Notation for Cusum ChartsFormulas for Cumulative SumsDefining the Decision Interval for a One-Sided Cusum SchemeDefining the V-Mask for a Two-Sided Cusum SchemeDesigning a Cusum SchemeCusum Charts Compared with Shewhart ChartsMethods for Estimating the Standard DeviationOutput Data SetsODS TablesODS GraphicsInput Data SetsMissing Values -
Examples

Creating a One-Sided Cusum Chart with a Decision Interval
See CUSONES1 in the SAS/QC Sample LibraryAn alternative to the V-mask cusum chart is the one-sided cusum chart with a decision interval, which is sometimes referred to as the “computational form of the cusum chart.” This example illustrates how you can create a one-sided cusum chart for individual measurements.
A can of oil is selected every hour for fifteen hours. The cans are weighed, and their weights are saved in a SAS data set
named Cans:[27]
data Cans; length comment $16; label Hour = 'Hour'; input Hour Weight comment $16. ; datalines; 1 8.024 2 7.971 3 8.125 4 8.123 5 8.068 6 8.177 Pump Adjusted 7 8.229 Pump Adjusted 8 8.072 9 8.066 10 8.089 11 8.058 12 8.147 13 8.141 14 8.047 15 8.125 ;
Suppose the problem is to detect a positive shift in the process mean of one standard deviation (![]() ) from the target of 8.100 ounces. Furthermore, suppose that
) from the target of 8.100 ounces. Furthermore, suppose that
-
a known value
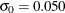 is available for the process standard deviation
is available for the process standard deviation
-
an in-control average run length (ARL) of approximately 100 is required
-
an ARL of approximately five is appropriate for detecting the shift
Table 6.3 indicates that these ARLs can be achieved with the decision interval h = 3 and the reference value k = 0.5. The following statements use these parameters to create the chart and tabulate the cusum scheme:
options nogstyle;
goptions ftext=swiss;
symbol v=dot color=salmon h=1.8 pct;
title "One-Sided Cusum Analysis";
proc cusum data=Cans;
xchart Weight*Hour /
mu0 = 8.100 /* target mean for process */
sigma0 = 0.050 /* known standard deviation */
delta = 1 /* shift to be detected */
h = 3 /* cusum parameter h */
k = 0.5 /* cusum parameter k */
scheme = onesided /* one-sided decision interval */
tableall /* table */
cinfill = ywh
cframe = bigb
cout = salmon
cconnect = salmon
climits = black
coutfill = bilg;
label Weight = 'Cusum of Weight';
run;
options gstyle;
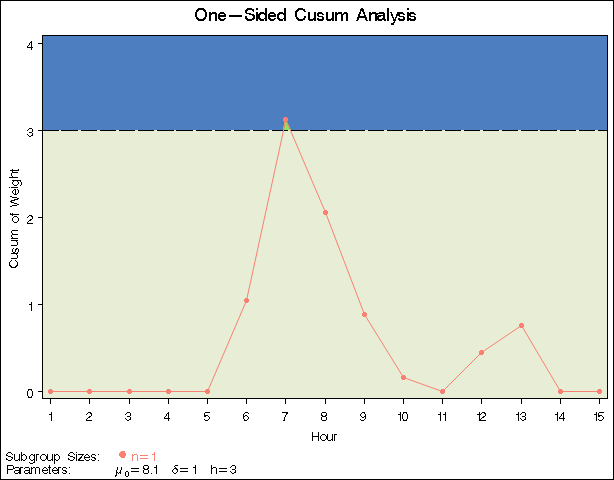
The NOGSTYLE system option causes ODS styles not to affect traditional graphics. Instead, the SYMBOL statement, GOPTIONS, and XCHART statement options control the appearance of the graph. The GSTYLE system option restores the use of ODS styles for traditional graphics produced subsequently. The chart is shown in Figure 6.6.
Figure 6.6: One-Sided Cusum Chart with Decision Interval
The cusum plotted at Hour=t is
|
|
where ![]() , and
, and ![]() is the standardized deviation of the tth measurement from the target.
is the standardized deviation of the tth measurement from the target.
|
|
The cusum ![]() is referred to as an upper cumulative sum. A shift is signaled at the seventh hour since
is referred to as an upper cumulative sum. A shift is signaled at the seventh hour since ![]() exceeds h. For further details, see One-Sided Cusum Schemes.
exceeds h. For further details, see One-Sided Cusum Schemes.
The option TABLEALL requests the tables shown in Figure 6.7, Figure 6.8, and Figure 6.9. The table in Figure 6.7 summarizes the cusum scheme, and it confirms that an in-control ARL of 117.6 and an ARL of 6.4 at ![]() are achieved with the specified h and k.
are achieved with the specified h and k.
Figure 6.7: Summary Table
| Cusum Parameters | |
|---|---|
| Process Variable | Weight (Cusum of Weight) |
| Subgroup Variable | Hour (Hour) |
| Scheme | One-Sided |
| Target Mean (Mu0) | 8.1 |
| Sigma0 | 0.05 |
| Delta | 1 |
| Nominal Sample Size | 1 |
| h | 3 |
| k | 0.5 |
| Average Run Length (Delta) | 6.40390895 |
| Average Run Length (0) | 117.595692 |
The table in Figure 6.8 tabulates the information displayed in Figure 6.6.
Figure 6.8: Tabulation of One-Sided Chart
| One-Sided Cusum Analysis |
| Cumulative Sum Chart Summary for Weight | |||||
|---|---|---|---|---|---|
| Hour | Subgroup Sample Size |
Individual Value |
Cusum | Decision Interval |
Decision Interval Exceeded |
| 1 | 1 | 8.0240000 | 0.0000000 | 3.0000 | |
| 2 | 1 | 7.9710000 | 0.0000000 | 3.0000 | |
| 3 | 1 | 8.1250000 | 0.0000000 | 3.0000 | |
| 4 | 1 | 8.1230000 | 0.0000000 | 3.0000 | |
| 5 | 1 | 8.0680000 | 0.0000000 | 3.0000 | |
| 6 | 1 | 8.1770000 | 1.0400000 | 3.0000 | |
| 7 | 1 | 8.2290000 | 3.1200000 | 3.0000 | Upper |
| 8 | 1 | 8.0720000 | 2.0600000 | 3.0000 | |
| 9 | 1 | 8.0660000 | 0.8800000 | 3.0000 | |
| 10 | 1 | 8.0890000 | 0.1600000 | 3.0000 | |
| 11 | 1 | 8.0580000 | 0.0000000 | 3.0000 | |
| 12 | 1 | 8.1470000 | 0.4400000 | 3.0000 | |
| 13 | 1 | 8.1410000 | 0.7600000 | 3.0000 | |
| 14 | 1 | 8.0470000 | 0.0000000 | 3.0000 | |
| 15 | 1 | 8.1250000 | 0.0000000 | 3.0000 | |
The table in Figure 6.9 presents the computational form of the cusum scheme described by Lucas (1976).
Figure 6.9: Computational Form of Cusum Scheme
| One-Sided Cusum Analysis |
| Computational Cumulative Sum for Weight | ||||
|---|---|---|---|---|
| Hour | Subgroup Sample Size |
Individual Value |
Upper Cusum |
Number of Consecutive Upper Sums > 0 |
| 1 | 1 | 8.0240000 | 0.0000000 | 0 |
| 2 | 1 | 7.9710000 | 0.0000000 | 0 |
| 3 | 1 | 8.1250000 | 0.0000000 | 0 |
| 4 | 1 | 8.1230000 | 0.0000000 | 0 |
| 5 | 1 | 8.0680000 | 0.0000000 | 0 |
| 6 | 1 | 8.1770000 | 1.0400000 | 1 |
| 7 | 1 | 8.2290000 | 3.1200000 | 2 |
| 8 | 1 | 8.0720000 | 2.0600000 | 3 |
| 9 | 1 | 8.0660000 | 0.8800000 | 4 |
| 10 | 1 | 8.0890000 | 0.1600000 | 5 |
| 11 | 1 | 8.0580000 | 0.0000000 | 0 |
| 12 | 1 | 8.1470000 | 0.4400000 | 1 |
| 13 | 1 | 8.1410000 | 0.7600000 | 2 |
| 14 | 1 | 8.0470000 | 0.0000000 | 0 |
| 15 | 1 | 8.1250000 | 0.0000000 | 0 |
Following the method of Lucas (1976), the process average at the out-of-control point (Hour=7) can be estimated as
|
|
||
|
|
|
|
|
|
|
|
where ![]() is the upper sum at
is the upper sum at Hour=7, and ![]() is the number of successive positive upper sums at
is the number of successive positive upper sums at Hour=7.