The Nonlinear Programming Solver

Example 10.6 Maximum Likelihood Weibull Estimation

The following data are taken from Lawless (1982, p. 193) and represent the number of days that it took rats that were painted with a carcinogen to develop carcinoma. The last two observations are censored data from a group of 19 rats. 

data pike;
   input days cens @@;
   datalines;
143  0  164  0  188  0  188  0
190  0  192  0  206  0  209  0
213  0  216  0  220  0  227  0
230  0  234  0  246  0  265  0
304  0  216  1  244  1
;

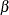Suppose you want to compute the maximum likelihood estimates of the scale parameter $\sigma $ ($\alpha $ in Lawless), the shape parameter $ c$ ($\beta $ in Lawless), and the location parameter 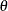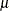$\theta $ ($\mu $ in Lawless). The observed likelihood function of the three-parameter Weibull transformation (Lawless 1982, p. 191) is

\[ L(\theta ,\sigma ,c) = \frac{c^ m}{\sigma ^ m} \prod _{i \in D} \left( \frac{t_ i - \theta }{\sigma } \right) ^{c-1} \prod _{i=1}^ n \exp \left( - \left( \frac{t_ i - \theta }{\sigma } \right) ^{c} \right) \]

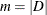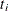where n is the number of individuals involved in the experiment, D is the set of individuals whose lifetimes are observed, $m=|D|$, and $t_ i$ is defined by the data set. Then the log-likelihood function is

\[ l(\theta ,\sigma ,c) = m \log c - mc \log \sigma + (c-1) \sum _{i \in D} \log (t_ i - \theta ) - \sum _{i=1}^ n \left( \frac{t_ i - \theta }{\sigma } \right) ^{c} \]

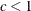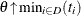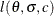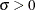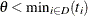For $c<1$, the logarithmic terms become infinite as $\theta \! \uparrow \! \min _{i\in D}(t_ i)$. That is, $l(\theta ,\sigma ,c)$ is unbounded. Thus our interest is restricted to c values greater than or equal to 1. Further, for the logarithmic terms to be defined, it is required that $\sigma >0$ and $\theta <\min _{i\in D}(t_ i)$.

The following PROC OPTMODEL call specifies the maximization of the log-likelihood function for the three-parameter Weibull estimation: 

proc optmodel;
   set OBS;
   num days {OBS};
   num cens {OBS};
   read data pike into OBS=[_N_] days cens;
   var sig   >= 1.0e-6 init 10;
   var c     >= 1.0e-6 init 10;
   var theta >= 0 <= min {i in OBS: cens[i] = 0} days[i] init 10;

   impvar fi {i in OBS} =
      (if cens[i] = 0 then
         log(c) - c * log(sig) + (c - 1) * log(days[i] - theta)
      )
    - ((days[i] - theta) / sig)^c;
   max logf = sum {i in OBS} fi[i];

   set VARS = 1.._NVAR_;
   num mycov {i in VARS, j in 1..i};
   solve with NLP / covest=(cov=2 covout=mycov);
   print sig c theta;
   print mycov;
   create data covdata from [i j]={i in VARS, j in 1..i}
      var_i=_VAR_[i].name var_j=_VAR_[j].name mycov;
quit;

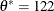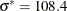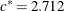The solution is displayed in Output 10.6.1. The solution that the NLP solver obtains closely matches the local maximum $\theta ^*=122$, $\sigma ^*=108.4$, and $c^*=2.712$ that are given in Lawless (1982, p. 193).

Output 10.6.1: Three-Parameter Weibull Estimation Results

The OPTMODEL Procedure

Problem Summary
Objective Sense Maximization
Objective Function logf
Objective Type Nonlinear
   
Number of Variables 3
Bounded Above 0
Bounded Below 2
Bounded Below and Above 1
Free 0
Fixed 0
   
Number of Constraints 0

Performance Information
Execution Mode Single-Machine
Number of Threads 4

Solution Summary
Solver NLP
Algorithm Interior Point
Objective Function logf
Solution Status Optimal
Objective Value -87.32424712
   
Optimality Error 5E-7
Infeasibility 0
   
Iterations 17
Presolve Time 0.00
Solution Time 0.03

sig c theta
108.38 2.7115 122.03

mycov
  1 2 3
1 1259.9694    
2 35.5375 1.3312  
3 -1056.9867 -31.6630 977.6173