The Nonlinear Programming Solver

Example 10.1 Solving Highly Nonlinear Optimization Problems

This example demonstrates the use of the NLP solver to solve the following highly nonlinear optimization problem, which appears in Hock and Schittkowski (1981):

\[ \begin{array}{ll} \displaystyle \mathop {\textrm{minimize}}& f(x) = 0.4 (x_{1}/x_{7})^{0.67} + 0.4 (x_{2}/x_{8})^{0.67} + 10 - x_{1} - x_{2} \\ \textrm{subject to}& 1 - 0.0588 x_5 x_7 - 0.1 x_1 \ge 0 \\ & 1 - 0.0588x_6 x_8 - 0.1 x_1 - 0.1 x_2 \ge 0 \\ & 1 - 4 x_3/x_5 - 2/(x_3^{0.71} x_5) - 0.0588 x_7/x_3^{1.3} \ge 0 \\ & 1 - 4 x_4/x_6 - 2/(x_4^{0.71} x_6) - 0.0588 x_8/x_4^{1.3} \ge 0 \\ & 0.1 \le f(x) \le 4.2 \\ & 0.1 \le x_ i \le 10, i=1,2, \ldots , 8 \end{array} \]

The initial point used is 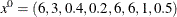$x^{0} = (6,3,0.4,0.2,6,6,1,0.5)$. You can call the NLP solver within PROC OPTMODEL to solve the problem by writing the following SAS statements: 

proc optmodel;
   var x{1..8} >= 0.1 <= 10;

   min f = 0.4*(x[1]/x[7])^0.67 + 0.4*(x[2]/x[8])^0.67 + 10 - x[1] - x[2];

   con c1: 1 - 0.0588*x[5]*x[7] - 0.1*x[1] >= 0;
   con c2: 1 - 0.0588*x[6]*x[8] - 0.1*x[1] - 0.1*x[2] >= 0;
   con c3: 1 - 4*x[3]/x[5] - 2/(x[3]^0.71*x[5]) - 0.0588*x[7]/x[3]^1.3 >= 0;
   con c4: 1 - 4*x[4]/x[6] - 2/(x[4]^0.71*x[6]) - 0.0588*x[8]/x[4]^1.3 >= 0;
   con c5: 0.1 <= f <= 4.2;

   /* starting point */
   x[1] = 6;
   x[2] = 3;
   x[3] = 0.4;
   x[4] = 0.2;
   x[5] = 6;
   x[6] = 6;
   x[7] = 1;
   x[8] = 0.5;

   solve with nlp / algorithm=activeset;
   print x;
 quit;

The summaries and the solution are shown in Output 10.1.1.

Output 10.1.1: Summaries and the Returned Solution

The OPTMODEL Procedure

Problem Summary
Objective Sense Minimization
Objective Function f
Objective Type Nonlinear
   
Number of Variables 8
Bounded Above 0
Bounded Below 0
Bounded Below and Above 8
Free 0
Fixed 0
   
Number of Constraints 5
Linear LE (<=) 0
Linear EQ (=) 0
Linear GE (>=) 0
Linear Range 0
Nonlinear LE (<=) 0
Nonlinear EQ (=) 0
Nonlinear GE (>=) 4
Nonlinear Range 1

Performance Information
Execution Mode Single-Machine
Number of Threads 4

Solution Summary
Solver NLP
Algorithm Active Set
Objective Function f
Solution Status Optimal
Objective Value 3.9511594994
   
Optimality Error 3.7138163E-7
Infeasibility 9.8486624E-7
   
Iterations 23
Presolve Time 0.00
Solution Time 0.03

[1] x
1 6.46511
2 2.23272
3 0.66740
4 0.59576
5 5.93268
6 5.52723
7 1.01332
8 0.40067