The NLP Procedure
- Overview
-
Getting Started

-
Syntax
 Functional SummaryDictionary of OptionsPROC NLP StatementARRAY StatementBOUNDS StatementBY StatementCRPJAC StatementDECVAR StatementGRADIENT StatementHESSIAN StatementINCLUDE StatementJACNLC StatementJACOBIAN StatementLABEL StatementLINCON StatementMATRIX StatementMIN, MAX, and LSQ StatementsMINQUAD and MAXQUAD StatementsNLINCON StatementPROFILE StatementProgram Statements
Functional SummaryDictionary of OptionsPROC NLP StatementARRAY StatementBOUNDS StatementBY StatementCRPJAC StatementDECVAR StatementGRADIENT StatementHESSIAN StatementINCLUDE StatementJACNLC StatementJACOBIAN StatementLABEL StatementLINCON StatementMATRIX StatementMIN, MAX, and LSQ StatementsMINQUAD and MAXQUAD StatementsNLINCON StatementPROFILE StatementProgram Statements -
Details
 Criteria for OptimalityOptimization AlgorithmsFinite-Difference Approximations of DerivativesHessian and CRP Jacobian ScalingTesting the Gradient SpecificationTermination CriteriaActive Set MethodsFeasible Starting PointLine-Search MethodsRestricting the Step LengthComputational ProblemsCovariance MatrixInput and Output Data SetsDisplayed OutputMissing ValuesComputational ResourcesMemory LimitRewriting NLP Models for PROC OPTMODEL
Criteria for OptimalityOptimization AlgorithmsFinite-Difference Approximations of DerivativesHessian and CRP Jacobian ScalingTesting the Gradient SpecificationTermination CriteriaActive Set MethodsFeasible Starting PointLine-Search MethodsRestricting the Step LengthComputational ProblemsCovariance MatrixInput and Output Data SetsDisplayed OutputMissing ValuesComputational ResourcesMemory LimitRewriting NLP Models for PROC OPTMODEL -
Examples

- References
JACNLC Statement
-
JACNLC variables;
The JACNLC statement defines the Jacobian matrix for the system of constraint functions 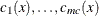 . The statements list the
. The statements list the 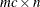 variable names which correspond to the elements
variable names which correspond to the elements 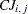 ,
, 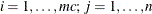 , of the Jacobian matrix by rows.
, of the Jacobian matrix by rows.
For example, the statements
nlincon c1-c3;
decvar x1-x2;
jacnlc cj1-cj6;
correspond to the Jacobian matrix
![\[ CJ = \left[ \begin{array}{cc} CJ1 & CJ2 \\ CJ3 & CJ4 \\ CJ5 & CJ6 \\ \end{array} \right] = \left[ \begin{array}{cc} \partial c_1/ \partial x_1 & \partial c_1/ \partial x_2 \\ \partial c_2/ \partial x_1 & \partial c_2/ \partial x_2 \\ \partial c_3/ \partial x_1 & \partial c_3/ \partial x_2 \\ \end{array} \right] \]](images/ormplpug_nlp0143.png)
The 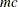 rows of the Jacobian matrix must be in the same order as the
rows of the Jacobian matrix must be in the same order as the 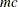 corresponding names of nonlinear constraints listed in the NLINCON
statement. The n columns of the Jacobian matrix must be in the same order as the n corresponding parameter names listed in the DECVAR
statement. To specify the values of nonzero derivatives, the variables specified in the JACNLC statement must be defined
on the left-hand side of algebraic expressions in programming statements.
corresponding names of nonlinear constraints listed in the NLINCON
statement. The n columns of the Jacobian matrix must be in the same order as the n corresponding parameter names listed in the DECVAR
statement. To specify the values of nonzero derivatives, the variables specified in the JACNLC statement must be defined
on the left-hand side of algebraic expressions in programming statements.
For example,
array cd[3,4] cd1-cd12;
nlincon c1-c3 >= 0;
jacnlc cd1-cd12;
c1 = 8 - x1 * x1 - x2 * x2 - x3 * x3 - x4 * x4 -
x1 + x2 - x3 + x4;
c2 = 10 - x1 * x1 - 2 * x2 * x2 - x3 * x3 - 2 * x4 * x4 +
x1 + x4;
c3 = 5 - 2 * x1 * x2 - x2 * x2 - x3 * x3 - 2 * x1 + x2 + x4;
cd[1,1]= -1 - 2 * x1; cd[1,2]= 1 - 2 * x2;
cd[1,3]= -1 - 2 * x3; cd[1,4]= 1 - 2 * x4;
cd[2,1]= 1 - 2 * x1; cd[2,2]= -4 * x2;
cd[2,3]= -2 * x3; cd[2,4]= 1 - 4 * x4;
cd[3,1]= -2 - 4 * x1; cd[3,2]= 1 - 2 * x2;
cd[3,3]= -2 * x3; cd[3,4]= 1;