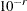The NLP Procedure

Finite-Difference Approximations of Derivatives

Subsections:

The FD= and FDHESSIAN= options specify the use of finite-difference approximations of the derivatives. The FD= option specifies that all derivatives are approximated using function evaluations, and the FDHESSIAN= option specifies that second-order derivatives are approximated using gradient evaluations.

Computing derivatives by finite-difference approximations can be very time-consuming, especially for second-order derivatives based only on values of the objective function ( FD= option). If analytical derivatives are difficult to obtain (for example, if a function is computed by an iterative process), you might consider one of the optimization techniques that uses first-order derivatives only (TECH= QUANEW, TECH= DBLDOG, or TECH= CONGRA).

Forward-Difference Approximations

The forward-difference derivative approximations consume less computer time but are usually not as precise as those using central-difference formulas.

  • First-order derivatives: n additional function calls are needed:

    \[ g_ i = \frac{\partial f}{\partial x_ i} = \frac{f(x + h_ ie_ i) - f(x)}{h_ i} \]

  • Second-order derivatives based on function calls only (Dennis and Schnabel 1983, p. 80, 104): for dense Hessian, 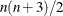$ n(n+3)/2$ additional function calls are needed:

    \[ \frac{\partial ^2 f}{\partial x_ i \partial x_ j} = \frac{f(x+h_ ie_ i+h_ je_ j) - f(x+h_ ie_ i) - f(x+h_ je_ j) + f(x)}{h_ j} \]

  • Second-order derivatives based on gradient calls (Dennis and Schnabel 1983, p. 103): n additional gradient calls are needed:

    \[ \frac{\partial ^2 f}{\partial x_ i \partial x_ j} = \frac{g_ i(x + h_ je_ j) - g_ i(x)}{2h_ j} + \frac{g_ j(x + h_ ie_ i) - g_ j(x)}{2h_ i} \]

Central-Difference Approximations

  • First-order derivatives: 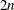$ 2n$ additional function calls are needed:

    \[ g_ i = \frac{\partial f}{\partial x_ i} = \frac{f(x + h_ ie_ i) - f(x - h_ ie_ i)}{2h_ i} \]

  • Second-order derivatives based on function calls only (Abramowitz and Stegun 1972, p. 884): for dense Hessian, 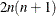$ 2n(n+1)$ additional function calls are needed:

    \begin{eqnarray*} \frac{\partial ^2 f}{\partial x^2_ i} & = & \frac{-f(x + 2h_ ie_ i) + 16f(x + h_ ie_ i) - 30f(x) + 16f(x - h_ ie_ i) - f(x - 2h_ ie_ i)}{12h^2_ i} \\[0.1in] \frac{\partial ^2 f}{\partial x_ i \partial x_ j} & = & \frac{f(x+h_ ie_ i+h_ je_ j) - f(x+h_ ie_ i-h_ je_ j) - f(x-h_ ie_ i+h_ je_ j) + f(x-h_ ie_ i-h_ je_ j)}{4h_ ih_ j} \nonumber \end{eqnarray*}

  • Second-order derivatives based on gradient: 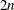$ 2n$ additional gradient calls are needed:

    \[ \frac{\partial ^2 f}{\partial x_ i \partial x_ j} = \frac{g_ i(x + h_ je_ j) - g_ i(x - h_ je_ j)}{4h_ j} + \frac{g_ j(x + h_ ie_ i) - g_ j(x - h_ ie_ i)}{4h_ i} \]

The FDIGITS= and CDIGITS= options can be used for specifying the number of accurate digits in the evaluation of objective function and nonlinear constraints. These specifications are helpful in determining an appropriate interval length h to be used in the finite-difference formulas.

The FDINT= option specifies whether the finite-difference intervals h should be computed using an algorithm of Gill, Murray, Saunders, and Wright (1983) or based only on the information of the FDIGITS= and CDIGITS= options. For FDINT= OBJ, the interval h is based on the behavior of the objective function; for FDINT= CON, the interval h is based on the behavior of the nonlinear constraints functions; and for FDINT= ALL, the interval h is based on the behaviors of both the objective function and the nonlinear constraints functions. Note that the algorithm of Gill, Murray, Saunders, and Wright (1983) to compute the finite-difference intervals 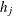$ h_ j$ can be very expensive in the number of function calls. If the FDINT= option is specified, it is currently performed twice, the first time before the optimization process starts and the second time after the optimization terminates.

If FDINT= is not specified, the step lengths 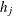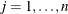$ h_ j$, $ j=1,\ldots ,n$, are defined as follows:

  • for the forward-difference approximation of first-order derivatives using function calls and second-order derivatives using gradient calls: $h_ j = \sqrt [2]{\eta _ j} (1 + |x_ j|)$,

  • for the forward-difference approximation of second-order derivatives that use only function calls and all central-difference formulas: $h_ j = \sqrt [3]{\eta _ j} (1 + |x_ j|)$,

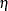where $\eta $ is defined using the FDIGITS= option:

  • If the number of accurate digits is specified with FDIGITS= r, $\eta $ is set to $ 10^{-r}$.

  • If FDIGITS= is not specified, $\eta $ is set to the machine precision $\epsilon $.

For FDINT= OBJ and FDINT= ALL, the FDIGITS= specification is used in computing the forward and central finite-difference intervals.

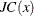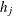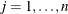If the problem has nonlinear constraints and the FD= option is specified, the first-order formulas are used to compute finite-difference approximations of the Jacobian matrix $ JC(x)$. You can use the CDIGITS= option to specify the number of accurate digits in the constraint evaluations to define the step lengths $ h_ j$, $ j=1,\ldots ,n$. For FDINT= CON and FDINT= ALL, the CDIGITS= specification is used in computing the forward and central finite-difference intervals.

Note: If you are unable to specify analytic derivatives and the finite-difference approximations provided by PROC NLP are not good enough to solve your problem, you may program better finite-difference approximations using the GRADIENT , JACOBIAN , CRPJAC , or HESSIAN statement and the program statements.