The CLP Procedure

LINCON Statement

  • LINCON linear_constraint-1 <…,linear_constraint-n>;

  • LINEAR linear_constraint-1 <…,linear_constraint-n>;

where linear_constraint has the form

linear_expression-l type linear_expression-r

where linear_expression has the form

<+|->linear_term-1 <…, (+|-) linear_term-n>

where linear_term has the form

(variable | number<* variable>)

The keyword type can be one of the following:

<, <=, =, >=, >, <>, LT, LE, EQ, GE, GT, NE

The LINCON statement allows for a very general specification of linear constraints. In particular, it allows for specification of the following types of equality or inequality constraints:

\[ \sum _{j=1}^ n a_{ij} x_ j \: \{ \le | < | = | \ge | > | \ne \} \: b_ i \quad \mr{for} \; i=1,\ldots ,m \]

For example, the constraint 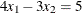$ 4x_1 - 3x_2 = 5$ can be expressed as 

var x1 x2;
lincon 4 * x1 - 3 * x2 = 5;

and the constraints

\[ \begin{array}{rcl} 10x_1 - x_2 & \geq & 10 \\ x_1 + 5x_2 & \ne & 15 \end{array} \]

can be expressed as 

var x1 x2;
lincon 10 <= 10 * x1 - x2,
       x1 + 5 * x2 <> 15;

Note that variables can be specified on either side of an equality or inequality in a LINCON statement. Linear constraints can also be specified by using the CONDATA= data set.

Regardless of the specification, you must define the variables by using a VARIABLE statement or implicitly by specifying the USECONDATAVARS= option.

User-specified scalar values are subject to rounding based upon a platform-dependent tolerance.