The CLP Procedure

Example 3.6 Scene Allocation Problem

The scene allocation problem consists of deciding when to shoot each scene of a movie in order to minimize the total production cost (Van Hentenryck 2002). Each scene involves a number of actors, and at most five scenes a day can be shot. All actors who appear in a scene must be present on the day the scene is shot. Each actor has a daily rate for each day spent in the studio, regardless of the number of scenes in which he or she appears on that day. The goal is to minimize the production costs of the studio.

The actor names, daily fees, and the scenes they appear are given in the SCENE data set shown in Output 3.6.1. The variables S_Var1, …, S_Var9 indicate the scenes in which the actor appears. For example, the first observation indicates that Patt’s daily fee is 26,481 and that Patt appears in scenes 2, 5, 7, 10, 11, 13, 15, and 17.

Output 3.6.1: The Scene Data Set

Obs	Number	Actor	DailyFee	S_Var1	S_Var2	S_Var3	S_Var4	S_Var5	S_Var6	S_Var7	S_Var8	S_Var9
1	1	Patt	26481	2	5	7	10	11	13	15	17	.
2	2	Casta	25043	4	7	9	10	13	16	19	.	.
3	3	Scolaro	30310	3	6	9	10	14	16	17	18	.
4	4	Murphy	4085	2	8	12	13	15	.	.	.	.
5	5	Brown	7562	2	3	12	17	.	.	.	.	.
6	6	Hacket	9381	1	2	12	13	18	.	.	.	.
7	7	Anderson	8770	5	6	14	.	.	.	.	.	.
8	8	McDougal	5788	3	5	6	9	10	12	15	16	18
9	9	Mercer	7423	3	4	5	8	9	16	.	.	.
10	10	Spring	3303	5	6	.	.	.	.	.	.	.
11	11	Thompson	9593	6	9	12	15	18	.	.	.	.

There are 19 scenes and at most five scenes can be filmed in one day, so at least four days are needed to schedule all the scenes (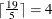 $\lceil \frac{19}{5} \rceil =4$ ). Let 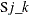$\mbox{S}j\_ k$ be a binary variable that equals 1 if scene j is shot on day k. Let 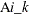$\mbox{A}i\_ k$ be another binary variable that equals 1 if actor i is present on day k. The variable 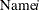$\mbox{Name}i$ is the name of the ith actor; 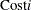$\mbox{Cost}i$ is the daily cost of the ith actor. 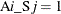$\mbox{A}i\_ \mbox{S}j = 1$ if actor i appears in scene j, and 0 otherwise.

The objective function representing the total production cost is given by

$\min \sum _{i=1}^{11}\sum _{k=1}^4 {Costi \times Ai\_ k }$

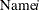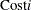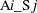The %SCENE macro first reads the data set scene and produces three sets of macro variables: $\mbox{Name}i$ , $\mbox{Cost}i$ , and $\mbox{A}i\_ \mbox{S}j$ . The data set cost is created next to specify the objective function. Finally, the CLP procedure is invoked. There are two sets of GCC constraints in the CLP call: one to make sure each scene is shot exactly once, and one to limit the number of scenes shot per day to be at least four and at most five. There are two sets of LINCON constraints: one to indicate that an actor must be present if any of his or her scenes are shot that day, and one for breaking symmetries to improve efficiency. Additionally, an OBJ statement specifies upper and lower bounds on the objective function to be minimized.

%macro scene;
   /* Ai_Sj=1 if actor i appears in scene j    */
   /* Ai_Sj=0 otherwise                        */
   /* Initialize to 0                          */
   %do i=1 %to 11; /* 11 actors */
      %do j=1 %to 19; /* 19 scenes */
         %let A&i._S&j=0;
      %end;
   %end;

   data scene_cost;
      set scene;
      keep DailyFee A;
      retain DailyFee A;
      do day=1 to 4;
         A='A'||left(strip(_N_))||'_'||left(strip(day));
         output;
      end;
      call symput("Name"||strip(_n_), Actor); /* read actor name */
      call symput("Cost"||strip(_n_), DailyFee); /* read actor cost */
      /* read whether an actor appears in a scene */
      %do i=1 %to 9; /* 9 scene variables in the data set */
         if S_Var&i > 0 then
            call symput("A"||strip(_n_)||"_S"||strip(S_Var&i), 1);
      %end;
   run;
   /* Create constraint data set which defines the objective function */
   proc transpose data=scene_cost out=cost(drop=_name_);
      var DailyFee;
      id A;
   run;
   data cost;
      set cost;
      _TYPE_='MIN';
      _RHS_=.;
   run;

   /* Find the minimum objective value.                   */
   proc clp condata=cost out=out varselect=maxc;
      /* Set lower and upper bounds for the objective value   */
      /* Lower bound: every actor appears on one day.         */
      /* Upper bound: every actor appears on all four days.   */
      obj lb=137739 ub=550956;

      /* Declare variables. */
      %do k=1 %to 4; /* 4 days */
      %do j=1 %to 19; /* 19 scenes */
         var S&j._&k=[0,1]; /* Indicates if scene j is shot on day k.   */
      %end;
      %do i=1 %to 11; /* 11 actors */
         var A&i._&k=[0,1]; /* Indicates if actor i is present on day k.*/
      %end;
      %end;

      /* Every scene is shot exactly once.*/
      %do j=1 %to 19;
         gcc (
            %do k=1 %to 4;
               S&j._&k
            %end;
            )=( (1, 1, 1) );
      %end;

      /* At least 4 and at most 5 scenes are shot per day. */
      %do k=1 %to 4;
         gcc (
            %do j=1 %to 19;
               S&j._&k
            %end;
            )=( (1, 4, 5) );
      %end;

      /* Actors for a scene must be present on day of shooting.*/
      %do k=1 %to 4;
         %do j=1 %to 19;
            %do i=1 %to 11;
               %if (&&A&i._S&j>0) %then %do;
                  lincon S&j._&k <= A&i._&k;
               %end;
            %end;
         %end;
      %end;

      /* Symmetry breaking constraints. Without loss of any generality, we */
      /* can assume Scene1 to be shot on day 1, Scene2 to be shot on day 1 */
      /* or day 2, and Scene3 to be shot on either day 1, day 2 or day 3.  */
      lincon S1_1 = 1, S1_2 = 0, S1_3 = 0, S1_4 = 0,
         S2_3 = 0, S2_4 = 0, S3_4 = 0;

      /* If Scene2 is shot on day 1,                */
      /* then Scene3 can be shot on day 1 or day 2. */
      lincon S2_1 + S3_3 <= 1;

   run;
   %put &_ORCLP_;

%mend scene;

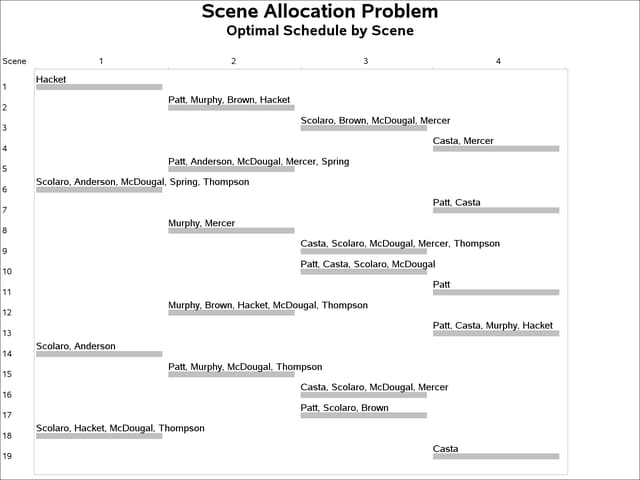
The optimal production cost is 334,144, as reported in the _ORCLP_ macro variable. The corresponding actor schedules and scene schedules are displayed in Output 3.6.2 and Output 3.6.3, respectively.

Output 3.6.2: Scene Allocation Problem: Actor Schedules

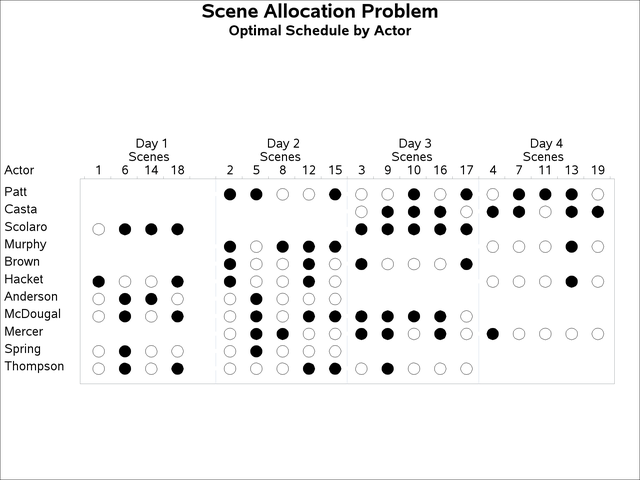
Output 3.6.3: Scene Allocation Problem: Scene Schedules