The CLP Procedure

ELEMENT Statement

ELEMENT element_constraint-1 <…element_constraint-n>;

An element_constraint is specified in the following form:

(index variable, (integer list), variable)

The ELEMENT statement specifies one or more element constraints. An element constraint enables you to define dependencies, not necessarily functional, between variables. The statement

ELEMENT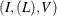 $(I, (L), V)$

sets the variable V to be equal to the Ith element in the list L. The list of integers 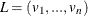$L = (v_1,...,v_ n)$ is a list of values that the variable V can take and are not necessarily distinct. The variable I is the index variable, and its domain is considered to be $[1, n]$ . Each time the domain of I is modified, the domain of V is updated and vice versa.

An element constraint enforces the following propagation rules:

$V=v \Leftrightarrow I \in \{ i_1, ..., i_ m\}$

where v is a value in the list L and 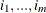$i_1, ..., i_ m$ are all the indices in L whose value is v.

The following statements use the element constraint to implement the quadratic function 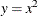$y=x^2$ :

proc clp out=clpout;
   var x=[1,5] y=[1,25];
   element (x,(1, 4, 9, 16, 25), y);
run;

An element constraint is equivalent to a conjunction of reify and linear constraints. For example, the preceding statements are equivalent to:


proc clp out=clpout;
        var x=[1,5] y=[1,25] (R1-R5)=[0,1];
        reify R1: (x=1);
        reify R1: (y=1);
        reify R2: (x=2);
        reify R2: (y=4);
        reify R3: (x=3);
        reify R3: (y=9);
        reify R4: (x=4);
        reify R4: (y=16);
        reify R5: (x=5);
        reify R5: (y=25);
        lincon R1 + R2 + R3 + R4 + R5 = 1;
run;

Element constraints can also be used to define positional mappings between two variables. For example, suppose the function 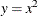$y=x^2$ is defined on only odd numbers in the interval $[-5, 5]$ . You can model this by using two element constraints and an artificial index variable:

   element (i, ( -5, -3, -1, 1, 3,  5), x)
           (i, ( 25,  9,  1, 1, 9, 25), y);

The list of values L can also be specified by using a convenient syntax of the form start TO end or start TO end BY increment. For example, the previous element specification is equivalent to:

   element (i, ( -5 to 5 by 2), x)
           (i, ( 25,  9,  1, 1, 9, 25), y);