The CLP Procedure

Round-robin tournaments (and variations of them) are a popular format in the scheduling of many sports league tournaments. In a single round-robin tournament, each team plays every other team just once. In a double round-robin (DRR) tournament, each team plays every other team twice: once at home and once away.

This particular example deals with a single round-robin tournament by modeling it as a scheduling CSP. A special case of a double round-robin tournament can be found in Example 3.12, "Scheduling a Major Basketball Conference" and features a different modeling approach.

Consider 14 teams that participate in a single round-robin tournament. Four rooms are provided for the tournament. Thus, 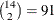games and 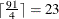time slots (rounds) need to be scheduled. Since each game requires two teams, a room, and an available time slot, you can regard each game as an activity, the two teams and the room as resources required by the activity, and the time slot as defined by the start and finish times of the activity.

In other words, you can treat this as a scheduling CSP with activities ACT_i_j where 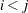, and resources TEAM1 through TEAM14 and ROOM1 through ROOM4. For a given i and j, activity ACT_i_j requires the resources TEAMi, TEAMj, and one of ROOM1 through ROOM4. The resulting start time for activity A_i_j is the time slot for the game between TEAMi and TEAMj and the assigned ROOM is the venue for the game.

The following SAS macro, %ROUND_ROBIN, uses the CLP procedure to solve this problem. The %ROUND_ROBIN macro uses the number of teams as a parameter.

The ACTDATA= data set defines all activities ACT_i_j with duration one. The RESOURCE statement declares the TEAM and ROOM resources. The REQUIRES statement defines the resource requirements for each activity ACT_i_j. The SCHEDULE statement defines the activity selection strategy as MINLS, which selects an activity with minimum late start time from the set of activities that begin prior to the earliest early finish time.

%macro round_robin(nteams);

   %let nrounds = %eval(%sysfunc(ceil((&nteams * (&nteams - 1)/2)/4)));

   data actdata;
      do i = 1 to &nteams - 1;
         do j = i + 1 to &nteams;
            _activity_ = compress('ACT_'||put(i,best.)||'_'||put(j,best.));
            _duration_ = 1;
            output;
         end;
      end;
   run;

   proc clp actdata = actdata schedule = schedule;
      schedule finish = &nrounds actselect=minls;
      resource (TEAM1-TEAM&nteams);
      resource (ROOM1-ROOM4);
      requires
         %do i = 1 %to &nteams - 1;
            %do j = &i + 1 %to &nteams;
               ACT_&i._&j = ( TEAM&i )
               ACT_&i._&j = ( TEAM&j )
               ACT_&i._&j = ( ROOM1, ROOM2, ROOM3, ROOM4)
            %end;
         %end;
      ;
      run;

   proc sort data=schedule;
      by start finish;
   run;

%mend round_robin;

%round_robin(14);

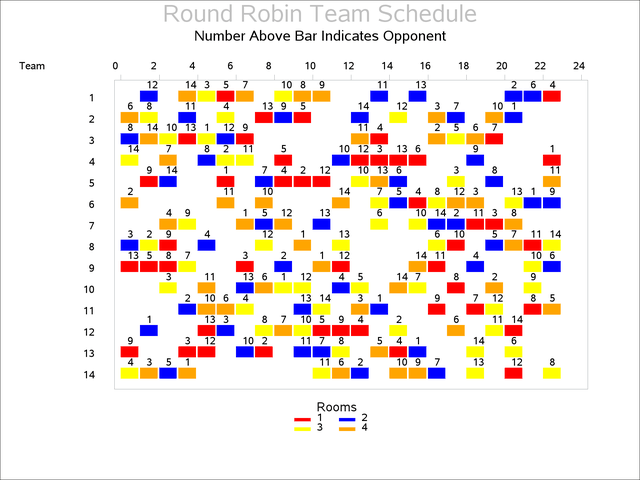
The resulting team schedule is displayed in Output 3.8.1. The vertical axis lists the teams, and the horizontal axis indicates the time slot of each game. The color of the bar indicates the room the game is played in, while the text above each bar identifies the opponent.

Another view of the complete schedule is the room schedule, which is shown in Output 3.8.2. The vertical axis lists each room, and the horizontal axis indicates the time slot of each game. The numbers inside each bar identify the team pairings for the corresponding room and time slot.