The CLP Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details

-
Examples
 Logic-Based PuzzlesAlphabet Blocks ProblemWork-Shift Scheduling ProblemA Nonlinear Optimization ProblemCar Painting ProblemScene Allocation ProblemCar Sequencing ProblemRound-Robin ProblemResource-Constrained Scheduling with Nonstandard Temporal ConstraintsScheduling with Alternate Resources10×10 Job Shop Scheduling ProblemScheduling a Major Basketball ConferenceBalanced Incomplete Block DesignProgressive Party ProblemStatement and Option Cross-Reference Table
Logic-Based PuzzlesAlphabet Blocks ProblemWork-Shift Scheduling ProblemA Nonlinear Optimization ProblemCar Painting ProblemScene Allocation ProblemCar Sequencing ProblemRound-Robin ProblemResource-Constrained Scheduling with Nonstandard Temporal ConstraintsScheduling with Alternate Resources10×10 Job Shop Scheduling ProblemScheduling a Major Basketball ConferenceBalanced Incomplete Block DesignProgressive Party ProblemStatement and Option Cross-Reference Table - References
The Constraint Satisfaction Problem
Many important problems in areas such as artificial intelligence (AI) and operations research (OR) can be formulated as constraint satisfaction problems. A CSP is defined by a finite set of variables that take values from finite domains and by a finite set of constraints that restrict the values that the variables can simultaneously take.
More formally, a CSP can be defined as a triple ![]() :
:
-
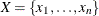 is a finite set of variables.
is a finite set of variables.
-
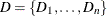 is a finite set of domains, where
is a finite set of domains, where 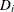 is a finite set of possible values that the variable
is a finite set of possible values that the variable 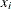 can take.
can take. 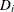 is known as the domain of variable
is known as the domain of variable 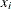 .
.
-
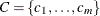 is a finite set of constraints that restrict the values that the variables can simultaneously take.
is a finite set of constraints that restrict the values that the variables can simultaneously take.
The domains need not represent consecutive integers. For example, the domain of a variable could be the set of all even numbers in the interval [0, 100]. A domain does not even need to be totally numeric. In fact, in a scheduling problem with resources, the values are typically multidimensional. For example, an activity can be considered as a variable, and each element of the domain would be an n-tuple that represents a start time for the activity and one or more resources that must be assigned to the activity that corresponds to the start time.
A solution to a CSP is an assignment of values to the variables in order to satisfy all the constraints. The problem amounts to finding one or more solutions, or possibly determining that a solution does not exist.
The CLP procedure can be used to find one or more (and in some instances, all) solutions to a CSP with linear, logical, global, and scheduling constraints. The numeric components of all variable domains are assumed to be integers.