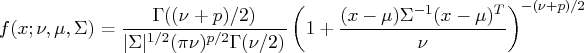| Module Library |
RANDMVT Function
generates a random sample from a multivariate
Student's ![]() distribution
distribution
- RANDMVT( N, DF, Mean, Cov )
The inputs are as follows:
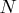
- is the number of desired observations sampled from the
multivariate Student's
 distribution.
distribution.
- DF
- is a scalar value representing the degrees of
freedom for the
 distribution.
distribution.
- Mean
- is a
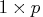 vector of means.
vector of means.
- Cov
- is a
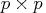 symmetric positive definite
variance-covariance matrix.
symmetric positive definite
variance-covariance matrix.
The RANDMVT function returns an
If
- the probability density function for
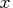 is
is
- if
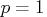 , the probability density function reduces to a univariate Student's
, the probability density function reduces to a univariate Student's 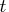 distribution.
distribution.
- the expected value of
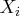 is
is 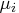 .
. - the covariance of
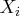 and
and 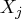 is
is
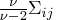 when
when 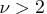 .
.
The following example generates 1000 samples from a two-dimensional ![]() distribution with 7 degrees of freedom, mean vector
distribution with 7 degrees of freedom, mean vector ![]() , and
covariance matrix S.
Each row of the returned matrix x is a row vector
sampled from the
, and
covariance matrix S.
Each row of the returned matrix x is a row vector
sampled from the ![]() distribution.
The example then computes the sample mean and covariance and compares
them with the expected values. Here are the code and the output:
distribution.
The example then computes the sample mean and covariance and compares
them with the expected values. Here are the code and the output:
call randseed(1);
N=1000;
DF = 4;
Mean = {1 2};
S = {1 1, 1 5};
x = RandMVT( N, DF, Mean, S );
SampleMean = x[:,];
n = nrow(x);
y = x - repeat( SampleMean, n );
SampleCov = y`*y / (n-1);
Cov = (DF/(DF-2)) * S;
print SampleMean Mean, SampleCov Cov;
SampleMean Mean
1.0768636 2.0893911 1 2
SampleCov Cov
1.8067811 1.8413406 2 2
1.8413406 9.7900638 2 10
In the preceding example, the columns (marginals) of x do
not follow univariate ![]() distributions. If you want a sample whose
marginals are univariate
distributions. If you want a sample whose
marginals are univariate ![]() , then you need to scale each column of
the output matrix:
, then you need to scale each column of
the output matrix:
x = RandMVT( N, DF, Mean, S );
StdX = x / sqrt(diag(S)); /* StdX columns are univariate t */
Equivalently, you can generate samples whose marginals are univariate
![]() by passing in a correlation matrix instead of a general covariance matrix.
by passing in a correlation matrix instead of a general covariance matrix.
For further details about sampling from the multivariate ![]() distribution, see
Kotz and Nadarajah (2004, pp. 1 - 11).
distribution, see
Kotz and Nadarajah (2004, pp. 1 - 11).
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.