GPROJECT Procedure
About Types of Map Projections
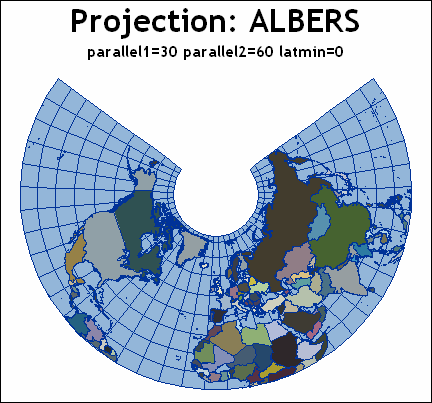
Albers' Equal-Area Projection
The Albers' projection
is a conic projection from the surface of the sphere to a cone secant
to the sphere, cutting it at two standard parallels of latitude. The
axis of the cone coincides with an extension of the polar axis of
the sphere. Each section of the resulting map bears a constant ratio
to the area of the sphere. In general, distortion in shape tends to
increase toward the poles in latitudes outside of the two standard
parallels.
Albers' Projection illustrates an Albers' equal-area projection of the northern
hemisphere.(footnote1)
The Albers' projection
is suitable for portraying areas of large and small east-to-west
extent and produces satisfactory results in most cases. However,
both standard parallels must lie on the same side of the equator,
so this method might not be suitable for map data sets of large north-to-south
extent that span the equator. For those map data sets, use the gnomonic
projection method.
Lambert's Conformal Projection
The Lambert's projection
is obtained from a secant cone in the same manner as Albers' projection.
In the Lambert's projection, meridians of longitude are straight lines
that radiate from the apex of the cone, while parallels of latitude
are concentric circles. The Lambert's projection is somewhat better
than the Albers' projection at representing the original shape of
projected unit areas, while the Albers' projection is somewhat better
at representing relative sizes of projected unit areas.
Lambert's Projection illustrates a Lambert's conformal projection of Europe.
The Lambert's projection
is ideal for navigational charts and maps of relatively small east-to-west
extent. However, as in the Albers' projection, both standard parallels
must lie on the same side of the equator, so this method might not
be suitable for map data sets that span the equator. For those map
data sets, use the gnomonic projection method.
Gnomonic Projection
The gnomonic projection
is a planar projection from the surface of the sphere directly onto
an imaginary plane tangent to the sphere at the map projection pole.
By default, the projection pole is placed at the center of the map
data set that is to be projected, but you can specify the projection
pole to be anywhere on the surface of the sphere. (See the POLELAT=latitude POLELONG=longitude.)
Gnomonic Projection illustrates a gnomonic projection of Africa.
In the gnomonic projection,
distortion increases as the distance from the map pole increases.
Because of this distortion, the PROC GPROJECT procedure deletes all
of the observations that lie more than 85 degrees from the map pole.
The gnomonic projection is best suited for mapping areas of small
east-to-west extent.
FOOTNOTE 1:The projection
examples in this topic include grid lines that were added with the
Annotate facility. See the Samples area at
support.sas.com for
an example of adding latitude and longitude lines to a map.[return]