The SEVERITY Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Predefined DistributionsCensoring and TruncationParameter Estimation MethodParameter InitializationEstimating Regression EffectsLevelization of Classification VariablesSpecification and Parameterization of Model EffectsEmpirical Distribution Function Estimation MethodsStatistics of FitDefining a Severity Distribution Model with the FCMP ProcedurePredefined Utility FunctionsScoring FunctionsCustom Objective FunctionsMultithreaded ComputationInput Data SetsOutput Data SetsDisplayed OutputODS Graphics
Predefined DistributionsCensoring and TruncationParameter Estimation MethodParameter InitializationEstimating Regression EffectsLevelization of Classification VariablesSpecification and Parameterization of Model EffectsEmpirical Distribution Function Estimation MethodsStatistics of FitDefining a Severity Distribution Model with the FCMP ProcedurePredefined Utility FunctionsScoring FunctionsCustom Objective FunctionsMultithreaded ComputationInput Data SetsOutput Data SetsDisplayed OutputODS Graphics -
Examples
 Defining a Model for Gaussian DistributionDefining a Model for the Gaussian Distribution with a Scale ParameterDefining a Model for Mixed-Tail DistributionsEstimating Parameters Using Cramér-von Mises EstimatorFitting a Scaled Tweedie Model with RegressorsFitting Distributions to Interval-Censored DataDefining a Finite Mixture Model That Has a Scale ParameterPredicting Mean and Value-at-Risk by Using Scoring FunctionsScale Regression with Rich Regression Effects
Defining a Model for Gaussian DistributionDefining a Model for the Gaussian Distribution with a Scale ParameterDefining a Model for Mixed-Tail DistributionsEstimating Parameters Using Cramér-von Mises EstimatorFitting a Scaled Tweedie Model with RegressorsFitting Distributions to Interval-Censored DataDefining a Finite Mixture Model That Has a Scale ParameterPredicting Mean and Value-at-Risk by Using Scoring FunctionsScale Regression with Rich Regression Effects - References
PROC SEVERITY supports formation of regression effects in the SCALEMODEL statement. A regression effect is formed from one or more regressor variables according to effect construction rules (parameterization). Each regression effect forms one element of ![]() in the linear model structure
in the linear model structure ![]() that affects the scale parameter. The SCALEMODEL statement in conjunction with the CLASS
statement supports a rich set of effects. In order to correctly interpret the results, you need to understand the specification
and parameterization of effects that are discussed in this section.
that affects the scale parameter. The SCALEMODEL statement in conjunction with the CLASS
statement supports a rich set of effects. In order to correctly interpret the results, you need to understand the specification
and parameterization of effects that are discussed in this section.
Effects are specified by a special notation that uses variable names and operators. There are two types of regressor variables: classification (or CLASS) variables and continuous variables. Classification variables can be either numeric or character and are specified in a CLASS statement. For more information, see the section Levelization of Classification Variables. A regressor variable that is not declared in the CLASS statement is assumed to be continuous.
Two primary operators (crossing and nesting) are used for combining the variables, and several additional operators are used to simplify effect specification. Operators are discussed in the section Effect Operators.
If you specify the CLASS statement, then PROC SEVERITY supports a general linear model (GLM) parameterization and a reference parameterization for the classification variables. The GLM parameterization is the default. For more information, see the sections GLM Parameterization of Classification Variables and Effects and Reference Parameterization.
Table 23.8 summarizes the operators that are available for selecting and constructing effects. These operators are discussed in the following sections.
Table 23.8: Available Effect Operators
|
Operator |
Example |
Description |
|---|---|---|
|
A*B |
Crosses the levels of the effects |
|
|
A(B) |
Nests A levels within B levels |
|
|
A | B | C |
Specifies all interactions |
|
|
A | B | C@2 |
Reduces interactions in bar effects |
|
|
A1-A10 |
Specifies sequentially numbered variables |
|
|
A: |
Specifies variables that have a common prefix |
|
|
A- -C |
Specifies sequential variables in data set order |
You can shorten the specification of a large factorial model by using the bar operator. For example, two ways of writing the model for a full three-way factorial model follow:
scalemodel A B C A*B A*C B*C A*B*C; scalemodel A|B|C;
When you use the bar (|), the right and left sides become effects, and the cross of them becomes an effect. Multiple bars are permitted. The expressions are expanded from left to right, using rules 2–4 from Searle (1971, p. 390).
-
Multiple bars are evaluated from left to right. For example,
A|B|Cis evaluated as follows:A|B|C
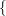
A|B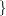 |
| C
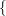
ABA*B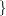 |
| C
ABA*BCA*CB*CA*B*C -
Crossed and nested groups of variables are combined. For example,
A(B) |C(D) generatesA*C(BD), among other terms. -
Duplicate variables are removed. For example,
A(C) |B(C) generatesA*B(CC), among other terms, and the extraCis removed. -
Effects are discarded if a variable occurs on both the crossed and nested parts of an effect. For example,
A(B) |B(DE) generatesA*B(BDE), but this effect is eliminated immediately.
You can also specify the maximum number of variables involved in any effect that results from bar evaluation by specifying that maximum number, preceded by an at sign (@), at the end of the bar effect. For example, the following specification selects only those effects that contain two or fewer variables:
scalemodel A|B|C@2;
The preceding example is equivalent to the following SCALEMODEL statement:
scalemodel A B C A*B A*C B*C;
More examples of using the bar and at sign operators follow:
|
|
is equivalent to |
|
|
|
is equivalent to |
|
|
|
is equivalent to |
|
|
|
is equivalent to |
|
|
|
is equivalent to |
|
|
|
is equivalent to |
|
|
|
is equivalent to |
|
Note: The preceding examples assume the following CLASS statement specification:
class A B C D;
You can simplify the specification of a large model when some of your variables have a common prefix by using the colon (:) operator and the dash (-) operator. The colon operator selects all variables that have a particular prefix, and the dash operator enables you to list variables that are numbered sequentially. For example, if your data set contains the variables X1 through X9, the following SCALEMODEL statements are equivalent:
scalemodel X1 X2 X3 X4 X5 X6 X7 X8 X9; scalemodel X1-X9; scalemodel X:;
If your data set contains only the three covariates X1, X2, and X9, then the colon operator selects all three variables:
scalemodel X:;
However, the following specification returns an error because X3 through X8 are not in the data set:
scalemodel X1-X9;
The double dash (- -) operator enables you to select variables that are stored sequentially in the SAS data set, whether or not they have a common prefix. You can use the CONTENTS procedure (see Base SAS Procedures Guide) to determine your variable ordering. For example, if you replace the dash in the preceding SCALEMODEL statement with a double dash, as follows, then all three variables are selected:
scalemodel X1--X9;
If your data set contains the variables A, B, and C, then you can use the double dash operator to select these variables by specifying the following:
scalemodel A--C;
Table 23.9 shows the types of effects that are available in the SEVERITY procedure; they are discussed in more detail in the following
sections. Let A, B, and C represent classification variables, and let X and Z represent continuous variables.
Table 23.9: Available Types of Effects
|
Effect |
Example |
Description |
|---|---|---|
|
X Z |
Continuous variables |
|
|
X*Z |
Interaction of continuous variables |
|
|
A B |
CLASS variables |
|
|
A*B |
Crossing of CLASS variables |
|
|
A(B) |
Main effect A nested within CLASS effect B |
|
|
X*A |
Crossing of continuous and CLASS variables |
|
|
X(A) |
Continuous variable X nested within CLASS variable A |
|
|
X*Z*A(B) |
Combinations of different types of effects |
Continuous variables or polynomial terms that involve them can be included in the model as continuous effects. An effect
that contains a single continuous variable is referred to as a singleton continuous effect, and an effect that contains an interaction of only continuous variables is referred to as a polynomial continuous effect. The actual values of such terms are included as columns of the relevant model matrices. You can use the bar operator
along with a continuous variable to generate polynomial effects. For example, X | X | X expands to X X*X X*X*X, which is a cubic model.
If a classification variable has m levels, the GLM parameterization generates m columns for its main effect in the model matrix. Each column is an indicator variable for a given level. The order of the columns is the sort order of the values of their levels and can be controlled by the ORDER= option in the CLASS statement.
Table 23.10 is an example where ![]() denotes the intercept and
denotes the intercept and A and B are classification variables that have two and three levels, respectively.
Table 23.10: Example of Main Effects
|
Data |
I |
|
|
|||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
A1 |
A2 |
B1 |
B2 |
B3 |
|||
|
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
|||
|
1 |
2 |
1 |
1 |
0 |
0 |
1 |
0 |
|||
|
1 |
3 |
1 |
1 |
0 |
0 |
0 |
1 |
|||
|
2 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
|||
|
2 |
2 |
1 |
0 |
1 |
0 |
1 |
0 |
|||
|
2 |
3 |
1 |
0 |
1 |
0 |
0 |
1 |
|||
There are usually more columns for these effects than there are degrees of freedom to estimate them. In other words, the GLM parameterization of main effects is singular.
Often a regression model includes interaction (crossed) effects to account for how the effect of a variable changes along
with the values of other variables. In an interaction, the terms are first reordered to correspond to the order of the variables
in the CLASS
statement. Thus, B*A becomes A*B if A precedes B in the CLASS
statement. Then, the GLM parameterization generates columns for all combinations of levels that occur in the data. The order
of the columns is such that the rightmost variables in the interaction change faster than the leftmost variables, as illustrated
in Table 23.11.
Table 23.11: Example of Interaction Effects
|
Data |
I |
|
|
|
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
A1 |
A2 |
B1 |
B2 |
B3 |
A1B1 |
A1B2 |
A1B3 |
A2B1 |
A2B2 |
A2B3 |
||||
|
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
||||
|
1 |
2 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
||||
|
1 |
3 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
||||
|
2 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
||||
|
2 |
2 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
||||
|
2 |
3 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
||||
In the matrix in Table 23.11, main-effects columns are not linearly independent of crossed-effects columns. In fact, the column space for the crossed effects contains the space of the main effect.
When your regression model contains many interaction effects, you might be able to code them more parsimoniously by using
the bar operator
( | ). The bar operator generates all possible interaction effects. For example, A | B | C expands to A B A*B C A*C B*C A*B*C. To eliminate higher-order interaction effects, use the at sign
(@) in conjunction with the bar operator. For example, A | B | C | D@2 expands to A B A*B C A*C B*C D A*D B*D C*D.
Nested effects are generated in the same manner as crossed effects. Hence, the design columns that are generated by the following two statements are the same (but the ordering of the columns is different):
scalemodel A B(A); scalemodel A A*B;
The nesting operator in PROC SEVERITY is more of a notational convenience than an operation that is distinct from crossing. Nested effects are usually characterized by the property that the nested variables do not appear as main effects. The order of the variables within nesting parentheses is made to correspond to the order of these variables in the CLASS statement. The order of the columns is such that variables outside the parentheses index faster than those inside the parentheses, and the rightmost nested variables index faster than the leftmost variables, as illustrated in Table 23.12.
Table 23.12: Example of Nested Effects
|
Data |
I |
|
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
A1 |
A2 |
B1A1 |
B2A1 |
B3A1 |
B1A2 |
B2A2 |
B3A2 |
|||
|
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|||
|
1 |
2 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|||
|
1 |
3 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|||
|
2 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|||
|
2 |
2 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|||
|
2 |
3 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
|||
When a continuous variable nests or crosses with a classification variable, the design columns are constructed by multiplying the continuous values into the design columns for the classification effect, as illustrated in Table 23.13.
Table 23.13: Example of Continuous-Nesting-Class Effects
|
Data |
I |
|
|
||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
A1 |
A2 |
X(A1) |
X(A2) |
|||
|
21 |
1 |
1 |
1 |
0 |
21 |
0 |
|||
|
24 |
1 |
1 |
1 |
0 |
24 |
0 |
|||
|
22 |
1 |
1 |
1 |
0 |
22 |
0 |
|||
|
28 |
2 |
1 |
0 |
1 |
0 |
28 |
|||
|
19 |
2 |
1 |
0 |
1 |
0 |
19 |
|||
|
23 |
2 |
1 |
0 |
1 |
0 |
23 |
|||
Continuous-by-class effects generate the same design columns as continuous-nesting-class effects. Table 23.14 shows the construction of the X*A effect. The two columns for this effect are the same as the columns for the X(A) effect in Table 23.13.
Table 23.14: Example of Continuous-by-Class Effects
|
Data |
I |
X |
|
|
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
X |
A1 |
A2 |
X*A1 |
X*A2 |
||||
|
21 |
1 |
1 |
21 |
1 |
0 |
21 |
0 |
||||
|
24 |
1 |
1 |
24 |
1 |
0 |
24 |
0 |
||||
|
22 |
1 |
1 |
22 |
1 |
0 |
22 |
0 |
||||
|
28 |
2 |
1 |
28 |
0 |
1 |
0 |
28 |
||||
|
19 |
2 |
1 |
19 |
0 |
1 |
0 |
19 |
||||
|
23 |
2 |
1 |
23 |
0 |
1 |
0 |
23 |
||||
An example that combines all the effects is X1*X2*A*B*C(D E). The continuous list comes first, followed by the crossed list, followed by the nested list in parentheses. PROC SEVERITY
might rename effects to correspond to ordering rules. For example, B*A(E D) might be renamed A*B(D E) to satisfy the following:
-
Classification variables that occur outside parentheses (crossed effects) are sorted in the order in which they appear in the CLASS statement.
-
Variables within parentheses (nested effects) are sorted in the order in which they appear in the CLASS statement.
The sequencing of the parameters that are generated by an effect is determined by the variables whose levels are indexed faster:
-
Variables in the crossed list index faster than variables in the nested list.
-
Within a crossed or nested list, variables to the right index faster than variables to the left.
For example, suppose a model includes four effects—A, B, C, and D—each of which has two levels, 1 and 2. Assume the CLASS
statement is
class A B C D;
Then the order of the parameters for the effect B*A(C D), which is renamed A*B(C D), is
![\[ \begin{array}{cccccc} A_1 B_1 C_1 D_1 \rightarrow & A_1 B_2 C_1 D_1 \rightarrow & A_2 B_1 C_1 D_1 \rightarrow & A_2 B_2 C_1 D_1 \rightarrow & \\ A_1 B_1 C_1 D_2 \rightarrow & A_1 B_2 C_1 D_2 \rightarrow & A_2 B_1 C_1 D_2 \rightarrow & A_2 B_2 C_1 D_2 \rightarrow & \\ A_1 B_1 C_2 D_1 \rightarrow & A_1 B_2 C_2 D_1 \rightarrow & A_2 B_1 C_2 D_1 \rightarrow & A_2 B_2 C_2 D_1 \rightarrow & \\ A_1 B_1 C_2 D_2 \rightarrow & A_1 B_2 C_2 D_2 \rightarrow & A_2 B_1 C_2 D_2 \rightarrow & A_2 B_2 C_2 D_2 \phantom{\rightarrow } \end{array} \]](images/etsug_severity0344.png)
Note that first the crossed effects B and A are sorted in the order in which they appear in the CLASS
statement so that A precedes B in the parameter list. Then, for each combination of the nested effects in turn, combinations of A and B appear. The B effect changes fastest because it is rightmost in the cross list. Then A changes next fastest, and D changes next fastest after that. The C effect changes most slowly because it is leftmost in the nested list.
Classification variables can be represented in the reference parameterization. Consider the classification variable A that has four values, 1, 2, 5, and 7. The reference parameterization generates three columns (one less than the number of
variable levels). The columns indicate group membership of the nonreference levels. For the reference level, the three dummy
variables have a value of 0. If the reference level is 7 (REF=’7’), the design columns for variable A are as shown in Table 23.15.
Parameter estimates of CLASS main effects that use the reference coding scheme estimate the difference in the effect of each nonreference level compared to the effect of the reference level.