The COUNTREG Procedure
- Overview
- Getting Started
-
Syntax
 Functional SummaryPROC COUNTREG StatementBAYES StatementBOUNDS StatementBY StatementCLASS StatementDISPMODEL StatementFREQ StatementINIT StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPERFORMANCE StatementPRIOR StatementRESTRICT StatementSCORE StatementSHOW StatementSTORE StatementWEIGHT StatementZEROMODEL Statement
Functional SummaryPROC COUNTREG StatementBAYES StatementBOUNDS StatementBY StatementCLASS StatementDISPMODEL StatementFREQ StatementINIT StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPERFORMANCE StatementPRIOR StatementRESTRICT StatementSCORE StatementSHOW StatementSTORE StatementWEIGHT StatementZEROMODEL Statement -
Details
 Specification of RegressorsMissing ValuesPoisson RegressionConway-Maxwell-Poisson RegressionNegative Binomial RegressionZero-Inflated Count Regression OverviewZero-Inflated Poisson RegressionZero-Inflated Conway-Maxwell-Poisson RegressionZero-Inflated Negative Binomial RegressionVariable SelectionPanel Data AnalysisBY Groups and Scoring with an Item StoreComputational ResourcesNonlinear Optimization OptionsCovariance Matrix TypesDisplayed OutputBayesian AnalysisPrior DistributionsAutomated MCMC AlgorithmOUTPUT OUT= Data SetOUTEST= Data SetODS Table NamesODS Graphics
Specification of RegressorsMissing ValuesPoisson RegressionConway-Maxwell-Poisson RegressionNegative Binomial RegressionZero-Inflated Count Regression OverviewZero-Inflated Poisson RegressionZero-Inflated Conway-Maxwell-Poisson RegressionZero-Inflated Negative Binomial RegressionVariable SelectionPanel Data AnalysisBY Groups and Scoring with an Item StoreComputational ResourcesNonlinear Optimization OptionsCovariance Matrix TypesDisplayed OutputBayesian AnalysisPrior DistributionsAutomated MCMC AlgorithmOUTPUT OUT= Data SetOUTEST= Data SetODS Table NamesODS Graphics -
Examples

- References
The BAYES statement controls the Metropolis sampling scheme that is used to obtain samples from the posterior distribution of the underlying model and data. You can specify the following options.
- AGGREGATION=WEIGHTED |NOWEIGHTED
-
specifies how multiple posterior samples should be aggregated.
- WEIGHTED
-
implements a weighted resampling scheme for the aggregation of multiple posterior chains. You can use this option when the posterior distribution is characterized by several very distinct posterior modes.
- NOWEIGHTED
-
aggregates multiple posterior chains without any adjustment. You can use this option when the posterior distribution is characterized by one or few relatively close posterior modes.
By default, AGGREGATION=NOWEIGHTED. For more information, see the section Aggregation of Multiple Chains.
- AUTOMCMC<=(automcmc-options)>
-
specifies an algorithm for the automated initialization of the MCMC sampling algorithm. For more information, see the section Automated Initialization of MCMC.
- ACCURACY=(accuracy-options)
-
customizes the behavior of the AUTOMCMC algorithm when you are searching for an accurate representation of the posterior distribution. By default, it implements the TARGETSTATS option. You can specify the following accuracy-options:
- ATTEMPTS=number
-
specifies the maximum number of attempts that are required in order to obtain accurate samples from the posterior distribution. By default, ATTEMPTS=10.
- TARGETESS=number
-
requests that the accuracy search be based on the effective sample size (ESS) analysis and specifies the minimum number of effective samples.
- TARGETSTATS<=(targetstats-option)>
-
requests that the accuracy search be based on the analysis of the posterior mean and a posterior quantile of interest. You can customize the behavior of the analysis of the posterior mean by adjusting the HEIDELBERGER suboptions. You can customize the behavior of the analysis of the posterior quantile by adjusting the RAFTERY suboptions. If you specify TARGETSTATS, you can also specify how the Raftery-Lewis test should be interpreted by using the following option:
- TOL=value
-
specifies the proportion of parameters that are required to be accurate. By default, TOL=0.95.
- MAXNMC=number
-
specifies the maximum number of posterior samples that the AUTOMCMC option allows. By default, MAXNMC=700000.
- RANDINIT<=(randinit-options)>
-
specifies random starting points for the MCMC algorithm. The starting points can be sampled around the maximum likelihood estimate and around the prior mean. You can specify the following randinit-options:
- MULTIPLIER=(value)
-
specifies the radius of the area where the starting points are sampled. For the starting points that are sampled around the maximum likelihood estimate, the radius equals the standard deviation of the maximum likelihood estimate multiplied by the multiplier value. For the starting points that are sampled around the prior mean, the radius equals the standard deviation of the prior distribution multiplied by the multiplier value. By default, MULTIPLIER=2.
- PROPORTION=(value)
-
specifies the proportion of starting points that are sampled around the maximum likelihood estimate and around the prior mean. By default, PROPORTION=0, which implies that all the initial points are sampled around the maximum likelihood estimate. If you choose to sample starting points around the prior mean, the convergence of the MCMC algorithm could be very slow.
- STATIONARITY=(stationarity-options)
-
customizes the behavior of the AUTOMCMC algorithm when you are trying to sample from the posterior distribution. You can specify the following stationarity-options:
-
DIAGNOSTICS=ALL | NONE | (keyword-list)
DIAG=ALL | NONE | (keyword-list) -
controls which diagnostics are produced. All the following diagnostics are produced by using DIAGNOSTICS=ALL. If you do not want any of these diagnostics, specify DIAGNOSTICS=NONE. If you want some but not all of the diagnostics, or if you want to change certain settings of these diagnostics, specify a subset of the following keywords. By default, DIAGNOSTICS=NONE.
- AUTOCORR<(LAGS=numeric-list)>
-
computes the autocorrelations at lags that are specified in the numeric-list. Elements in the numeric-list are truncated to integers, and repeated values are removed. If you do not specify the LAGS= option, autocorrelations of lags 1, 5, and 10 are computed.
- ESS
-
computes Carlin’s estimate of the effective sample size, the correlation time, and the efficiency of the chain for each parameter.
- GEWEKE<(geweke-options)>
-
computes the Geweke spectral density diagnostics, which are essentially a two-sample t test between the first
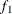 portion and the last
portion and the last 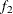 portion of the chain. The default is
portion of the chain. The default is 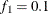 and
and 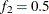 , but you can choose other fractions by using the following geweke-options:
, but you can choose other fractions by using the following geweke-options:
- HEIDELBERGER<(heidel-options)>
-
computes the Heidelberger-Welch diagnostic for each variable, which consists of a stationarity test of the null hypothesis that the sample values form a stationary process. If the stationarity test is not rejected, a halfwidth test is then performed. Optionally, you can specify one or more of the following heidel-options:
- SALPHA=value
-
specifies the
 level
level 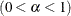 for the stationarity test. By default, SALPHA=0.05.
for the stationarity test. By default, SALPHA=0.05.
- HALPHA=value
-
specifies the
 level
level 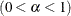 for the halfwidth test. By default, HALPHA=0.1.
for the halfwidth test. By default, HALPHA=0.1.
- EPS=value
-
specifies a positive number
 such that if the halfwidth is less than
such that if the halfwidth is less than  times the sample mean of the retained iterates, the halfwidth test is passed. By default, EPS=0.05.
times the sample mean of the retained iterates, the halfwidth test is passed. By default, EPS=0.05.
-
MCSE
MCERROR -
computes the Monte Carlo standard error for each parameter. The Monte Carlo standard error, which measures the simulation accuracy, is the standard error of the posterior mean estimate and is calculated as the posterior standard deviation divided by the square root of the effective sample size.
- RAFTERY<(raftery-options)>
-
computes the Raftery-Lewis diagnostics, which evaluate the accuracy of the estimated quantile (
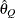 for a given
for a given 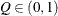 ) of a chain.
) of a chain. 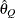 can achieve any degree of accuracy when the chain is allowed to run for a long time. The computation is stopped when the
estimated probability
can achieve any degree of accuracy when the chain is allowed to run for a long time. The computation is stopped when the
estimated probability 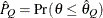 reaches within
reaches within 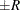 of the value Q with probability S; that is,
of the value Q with probability S; that is, 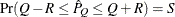 . The following raftery-options enable you to specify
. The following raftery-options enable you to specify 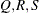 , and a precision level
, and a precision level  for the test:
for the test:
- QUANTILE | Q=value
-
specifies the order (a value between 0 and 1) of the quantile of interest. By default, Q=0.025.
- ACCURACY | R=value
-
specifies a small positive number as the margin of error for measuring the accuracy of estimation of the quantile. By default, R=0.005.
- PROBABILITY | S=value
-
specifies the probability of attaining the accuracy of the estimation of the quantile. By default, S=0.95.
- EPSILON | EPS=value
-
specifies the tolerance level (a small positive number) for the stationary test. By default, EPS=0.001.
- MAXTUNE=number
-
specifies the maximum number of tuning phases. By default, MAXTUNE=24.
- MINTUNE=number
-
specifies the minimum number of tuning phases. By default, MINTUNE=2.
- NBI=number
-
specifies the number of burn-in iterations before the chains are saved. By default, NBI=1000.
- NMC=number
-
specifies the number of iterations after the burn-in. By default, NMC=1000.
-
NTRDS=number
THREADS=number -
specifies the number of threads to be used. The number of threads cannot exceed the number of computer cores available. Each core samples the number of iterations that is specified by the NMC= option. By default, NTRDS=1.
- NTU=number
-
specifies the number of samples for each tuning phase. By default, NTU=500.
- OUTPOST=SAS-data-set
-
names the SAS data set to contain the posterior samples. Alternatively, you can create the output data set by specifying an ODS OUTPUT statement as follows:
- PROPCOV=value
-
specifies the method to use in constructing the initial covariance matrix for the Metropolis-Hastings algorithm. The quasi-Newton (PROPCOV=QUANEW) and Nelder-Mead simplex (PROPCOV=NMSIMP) methods find numerically approximated covariance matrices at the optimum of the posterior density function with respect to all continuous parameters. The tuning phase starts at the optimized values; in some problems, this can greatly increase convergence performance. If the approximated covariance matrix is not positive definite, then an identity matrix is used instead.
You can specify the following values:
- CONGRA
-
performs a conjugate-gradient optimization.
- DBLDOG
-
performs a version of double-dogleg optimization.
- NEWRAP
-
performs a Newton-Raphson optimization that combines a line-search algorithm with ridging.
- NMSIMP
-
performs a Nelder-Mead simplex optimization.
- NRRIDG
-
performs a Newton-Raphson optimization with ridging.
- QUANEW
-
performs a quasi-Newton optimization.
- TRUREG
-
performs a trust-region optimization.
- SAMPLING=MULTIMETROPOLIS |UNIMETROPOLIS
-
specifies how to sample from the posterior distribution.
- MULTIMETROPOLIS
-
implements a Metropolis sampling scheme in a single block that contains all the parameters of the model.
- UNIMETROPOLIS
-
implements a Metropolis sampling scheme in multiple blocks, one for each parameter of the model.
By default, SAMPLING=MULTIMETROPOLIS.
- SEED=number
-
specifies an integer seed in the range 1 to
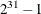 for the random number generator in the simulation. Specifying a seed enables you to reproduce identical Markov chains for
the same specification. If you do not specify the SEED= option, or if you specify SEED=0, a random seed is derived from the
time of day, which is read from the computer’s clock.
for the random number generator in the simulation. Specifying a seed enables you to reproduce identical Markov chains for
the same specification. If you do not specify the SEED= option, or if you specify SEED=0, a random seed is derived from the
time of day, which is read from the computer’s clock.
- SIMTIME
-
STATISTICS<(global-options)>=ALL | NONE | keyword | (keyword-list)
STATS<(global-options)>=ALL | NONE | keyword | (keyword-list) -
controls the number of posterior statistics that are produced. Specifying STATISTICS=ALL is equivalent to specifying STATISTICS=(CORR COV INTERVAL PRIOR SUMMARY). If you do not want any posterior statistics, specify STATISTICS=NONE. By default, STATISTICS=(SUMMARY INTERVAL).
You can specify the following global-options:
- ALPHA=numeric-list
-
controls the probabilities of the credible intervals. The values in the numeric-list must be between 0 and 1. Each ALPHA= value produces a pair of 100(1–ALPHA)% equal-tail and HPD intervals for each parameter. By default, ALPHA=0.05, which yields the 95% credible intervals for each parameter.
- PERCENT=numeric-list
-
requests the percentile points of the posterior samples. The values in the numeric-list must be between 0 and 100. By default, PERCENT=25, 50, 75, which yields the 25th, 50th, and 75th percentile points, respectively, for each parameter.
You can specify the following keywords:
- CORR
-
produces the posterior correlation matrix.
- COV
-
produces the posterior covariance matrix.
- INTERVAL
-
produces equal-tail credible intervals and HPD intervals. The default is to produce the 95% equal-tail credible intervals and 95% HPD intervals, but you can use the ALPHA= global-option to request intervals of any probabilities.
- NONE
-
suppresses printing of all summary statistics.
- PRIOR
-
produces a summary table of the prior distributions that are used in the Bayesian analysis.
- SUMMARY
-
produces the means, standard deviations, and percentile points (25th, 50th, and 75th) of the posterior samples. You can use the global PERCENT= global-option to request specific percentile points.
-
THIN=number
THINNING=number -
controls the thinning of the Markov chain. Only one in every k samples is used when THIN=k, and if NBI=
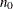 and NMC=n, the number of samples that are kept is
and NMC=n, the number of samples that are kept is
![\[ \biggl \lfloor \frac{n_0+n}{k} \biggr \rfloor - \biggl \lfloor \frac{n_0}{k} \biggr \rfloor \]](images/etsug_countreg0036.png)
where
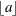 represents the integer part of the number a. By default, THIN=1.
represents the integer part of the number a. By default, THIN=1.