The COUNTREG Procedure
- Overview
- Getting Started
-
Syntax
 Functional SummaryPROC COUNTREG StatementBAYES StatementBOUNDS StatementBY StatementCLASS StatementDISPMODEL StatementFREQ StatementINIT StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPERFORMANCE StatementPRIOR StatementRESTRICT StatementSCORE StatementSHOW StatementSTORE StatementWEIGHT StatementZEROMODEL Statement
Functional SummaryPROC COUNTREG StatementBAYES StatementBOUNDS StatementBY StatementCLASS StatementDISPMODEL StatementFREQ StatementINIT StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPERFORMANCE StatementPRIOR StatementRESTRICT StatementSCORE StatementSHOW StatementSTORE StatementWEIGHT StatementZEROMODEL Statement -
Details
 Specification of RegressorsMissing ValuesPoisson RegressionConway-Maxwell-Poisson RegressionNegative Binomial RegressionZero-Inflated Count Regression OverviewZero-Inflated Poisson RegressionZero-Inflated Conway-Maxwell-Poisson RegressionZero-Inflated Negative Binomial RegressionVariable SelectionPanel Data AnalysisBY Groups and Scoring with an Item StoreComputational ResourcesNonlinear Optimization OptionsCovariance Matrix TypesDisplayed OutputBayesian AnalysisPrior DistributionsAutomated MCMC AlgorithmOUTPUT OUT= Data SetOUTEST= Data SetODS Table NamesODS Graphics
Specification of RegressorsMissing ValuesPoisson RegressionConway-Maxwell-Poisson RegressionNegative Binomial RegressionZero-Inflated Count Regression OverviewZero-Inflated Poisson RegressionZero-Inflated Conway-Maxwell-Poisson RegressionZero-Inflated Negative Binomial RegressionVariable SelectionPanel Data AnalysisBY Groups and Scoring with an Item StoreComputational ResourcesNonlinear Optimization OptionsCovariance Matrix TypesDisplayed OutputBayesian AnalysisPrior DistributionsAutomated MCMC AlgorithmOUTPUT OUT= Data SetOUTEST= Data SetODS Table NamesODS Graphics -
Examples

- References
The most widely used model for count data analysis is Poisson regression. This assumes that ![]() , given the vector of covariates
, given the vector of covariates ![]() , is independently Poisson-distributed with
, is independently Poisson-distributed with
and the mean parameter (that is, the mean number of events per period) is given by
where ![]() is a
is a ![]() parameter vector. (The intercept is
parameter vector. (The intercept is ![]() ; the coefficients for the k regressors are
; the coefficients for the k regressors are ![]() .) Taking the exponential of
.) Taking the exponential of ![]() ensures that the mean parameter
ensures that the mean parameter ![]() is nonnegative. It can be shown that the conditional mean is given by
is nonnegative. It can be shown that the conditional mean is given by
The name log-linear model is also used for the Poisson regression model because the logarithm of the conditional mean is linear in the parameters:
Note that the conditional variance of the count random variable is equal to the conditional mean in the Poisson regression model:
The equality of the conditional mean and variance of ![]() is known as equidispersion.
is known as equidispersion.
The marginal effect of a regressor is given by
Thus, a one-unit change in the jth regressor leads to a proportional change in the conditional mean ![]() of
of ![]() .
.
The standard estimator for the Poisson model is the maximum likelihood estimator (MLE). Because the observations are independent, the log-likelihood function is written as
where ![]() is defined as follows:
is defined as follows:
- 1
-
if neither the WEIGHT nor FREQ statement is used.
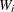
-
where
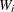 are the nonnormalized values of the variable that are specified in the WEIGHT statement in which the NONORMALIZE option is
specified.
are the nonnormalized values of the variable that are specified in the WEIGHT statement in which the NONORMALIZE option is
specified.
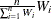
-
where
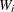 are the nonnormalized values of the variable that is specified in the WEIGHT statement.
are the nonnormalized values of the variable that is specified in the WEIGHT statement.
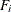
-
where
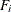 are the values of the variable that is specified in the FREQ statement.
are the values of the variable that is specified in the FREQ statement.
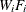
-
if both the WEIGHT statement, without the NONORMALIZE option, and the FREQ statement are specified.
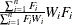
-
if both the FREQ and WEIGHT statements are specified.
The gradient and the Hessian are, respectively,
The Poisson model has been criticized for its restrictive property that the conditional variance must equal the conditional mean. Real-life data are often characterized by overdispersion (that is, the variance exceeds the mean). Allowing for overdispersion can improve model predictions because the Poisson restriction of equal mean and variance results in the underprediction of zeros when overdispersion exists. The most commonly used model that accounts for overdispersion is the negative binomial model. Conway-Maxwell-Poisson regression enables you to model both overdispersion and underdispersion.