The COUNTREG Procedure
- Overview
- Getting Started
-
Syntax
 Functional SummaryPROC COUNTREG StatementBAYES StatementBOUNDS StatementBY StatementCLASS StatementDISPMODEL StatementFREQ StatementINIT StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPERFORMANCE StatementPRIOR StatementRESTRICT StatementSCORE StatementSHOW StatementSTORE StatementWEIGHT StatementZEROMODEL Statement
Functional SummaryPROC COUNTREG StatementBAYES StatementBOUNDS StatementBY StatementCLASS StatementDISPMODEL StatementFREQ StatementINIT StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPERFORMANCE StatementPRIOR StatementRESTRICT StatementSCORE StatementSHOW StatementSTORE StatementWEIGHT StatementZEROMODEL Statement -
Details
 Specification of RegressorsMissing ValuesPoisson RegressionConway-Maxwell-Poisson RegressionNegative Binomial RegressionZero-Inflated Count Regression OverviewZero-Inflated Poisson RegressionZero-Inflated Conway-Maxwell-Poisson RegressionZero-Inflated Negative Binomial RegressionVariable SelectionPanel Data AnalysisBY Groups and Scoring with an Item StoreComputational ResourcesNonlinear Optimization OptionsCovariance Matrix TypesDisplayed OutputBayesian AnalysisPrior DistributionsAutomated MCMC AlgorithmOUTPUT OUT= Data SetOUTEST= Data SetODS Table NamesODS Graphics
Specification of RegressorsMissing ValuesPoisson RegressionConway-Maxwell-Poisson RegressionNegative Binomial RegressionZero-Inflated Count Regression OverviewZero-Inflated Poisson RegressionZero-Inflated Conway-Maxwell-Poisson RegressionZero-Inflated Negative Binomial RegressionVariable SelectionPanel Data AnalysisBY Groups and Scoring with an Item StoreComputational ResourcesNonlinear Optimization OptionsCovariance Matrix TypesDisplayed OutputBayesian AnalysisPrior DistributionsAutomated MCMC AlgorithmOUTPUT OUT= Data SetOUTEST= Data SetODS Table NamesODS Graphics -
Examples

- References
-
Abramowitz, M. and Stegun, A. (1970), Handbook of Mathematical Functions, New York: Dover Press.
-
Amemiya, T. (1985), Advanced Econometrics, Cambridge, MA: Harvard University Press.
-
Cameron, A. C. and Trivedi, P. K. (1986), “Econometric Models Based on Count Data: Comparisons and Applications of Some Estimators and Tests,” Journal of Applied Econometrics, 1, 29–53.
-
Cameron, A. C. and Trivedi, P. K. (1998), Regression Analysis of Count Data, Cambridge: Cambridge University Press.
-
Conway, R. W. and Maxwell, W. L. (1962), “A Queuing Model with State Dependent Service Rates,” Journal of Industrial Engineering, 12, 132–136.
-
Fan, J. and Li, R. (2001), “Variable Selection via Nonconcave Penalized Likelihood and Its Oracle Properties,” Journal of the American Statistical Association, 96, 1348–1360.
-
Gelman, A., Carlin, J. B., Stern, H. S., and Rubin, D. B. (2004), Bayesian Data Analysis, 2nd Edition, London: Chapman & Hall.
-
Godfrey, L. G. (1988), Misspecification Tests in Econometrics, Cambridge: Cambridge University Press.
-
Greene, W. H. (1994), “Accounting for Excess Zeros and Sample Selection in Poisson and Negative Binomial Regression Models,” Working paper 94-10, Leonard N. Stern School of Business, Department of Economics, New York University.
URL http://ideas.repec.org/p/ste/nystbu/94-10.html -
Greene, W. H. (2000), Econometric Analysis, 4th Edition, Upper Saddle River, NJ: Prentice-Hall.
-
Guikema, S. D. and Coffelt, J. P. (2008), “A Flexible Count Data Regression Model for Risk Analysis,” Risk Analysis, 28, 213–223.
-
Hausman, J. A., Hall, B. H., and Griliches, Z. (1984), “Econometric Models for Count Data with an Application to the Patents-R&D Relationship,” Econometrica, 52, 909–938.
-
King, G. (1989a), “A Seemingly Unrelated Poisson Regression Model,” Sociological Methods and Research, 17, 235–255.
-
King, G. (1989b), Unifying Political Methodology: The Likelihood Theory and Statistical Inference, Cambridge: Cambridge University Press.
-
Lambert, D. (1992), “Zero-Inflated Poisson Regression with an Application to Defects in Manufacturing,” Technometrics, 34, 1–14.
-
LaMotte, L. R. (1994), “A Note on the Role of Independence in t Statistics Constructed from Linear Statistics in Regression Models,” American Statistician, 48, 238–240.
-
Long, J. S. (1997), Regression Models for Categorical and Limited Dependent Variables, Thousand Oaks, CA: Sage Publications.
-
Lord, D., Guikema, S. D., and Geedipally, S. R. (2008), “Application of the Conway-Maxwell-Poisson Generalized Linear Model for Analyzing Motor Vehicle Crashes,” Accident Analysis and Prevention, 40, 1123–1134.
-
Park, M. Y. and Hastie, T. J. (2007), “
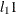 -Regularization Path Algorithm for Generalized Linear Models,” Journal of the Royal Statistical Society, Series B, 69, 659–677.
-Regularization Path Algorithm for Generalized Linear Models,” Journal of the Royal Statistical Society, Series B, 69, 659–677.
-
Roberts, G. O., Gelman, A., and Gilks, W. R. (1997), “Weak Convergence and Optimal Scaling of Random Walk Metropolis Algorithms,” Annals of Applied Probability, 7, 110–120.
-
Roberts, G. O. and Rosenthal, J. S. (2001), “Optimal Scaling for Various Metropolis-Hastings Algorithms,” Statistical Science, 16, 351–367.
-
Schervish, M. J. (1995), Theory of Statistics, New York: Springer-Verlag.
-
Searle, S. R. (1971), Linear Models, New York: John Wiley & Sons.
-
Shmueli, G., Minka, T. P., Kadane, J. B., Borle, S., and Boatwright, P. (2005), “A Useful Distribution for Fitting Discrete Data: Revival of the Conway-Maxwell-Poisson Distribution,” Journal of the Royal Statistical Society, Series C, 54, 127–142.
-
Winkelmann, R. (2000), Econometric Analysis of Count Data, Berlin: Springer-Verlag.
-
Zou, H. and Li, R. (2008), “One-Step Sparse Estimates in Nonconcave Penalized Likelihood Models,” Annals of Statistics, 36, 1509–1533.