The COUNTREG Procedure

Zero-Inflated Poisson Regression

Subsections:

In the zero-inflated Poisson (ZIP) regression model, the data generation process that is referred to earlier as Process 2 is

\[ g(y_{i}) = \frac{\exp (-\mu _{i})\mu _{i}^{y_{i}}}{y_{i}!} \]

where $\mu _ i=e^{\mathbf{x}_{i}'\bbeta }$. Thus the ZIP model is defined as

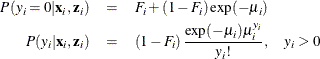
\begin{eqnarray*} P(y_{i}=0|\mathbf{x}_{i},\mathbf{z}_{i}) & =& F_{i} + \left(1 - F_{i}\right)\exp (-\mu _{i}) \\ P(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i}) & =& \left(1- F_{i} \right)\frac{\exp (-\mu _{i}) \mu _ i^{y_{i}}}{y_{i}!},\quad y_{i}>0 \end{eqnarray*}

The conditional expectation and conditional variance of $y_{i}$ are given by

\[ E(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i}) = \mu _{i}(1 -F_{i}) \]
\[ V(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i}) = E(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i})(1+\mu _{i}F_{i}) \]

Note that the ZIP model (as well as the ZINB model) exhibits overdispersion because $V(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i}) >E(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i})$.

In general, the log-likelihood function of the ZIP model is

\[ \mathcal{L} = \sum _{i=1}^{N}w_ i\ln \left[ P(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i}) \right] \]

After a specific link function (either logistic or standard normal) for the probability $\varphi _{i}$ is chosen, it is possible to write the exact expressions for the log-likelihood function and the gradient.

ZIP Model with Logistic Link Function

First, consider the ZIP model in which the probability $\varphi _{i}$ is expressed using a logistic link function—namely,

\[ \varphi _{i}=\frac{\exp (\mathbf{z}_{i}'\bgamma )}{1+\exp (\mathbf{z}_{i}'\bgamma )} \]

The log-likelihood function is

\begin{eqnarray*} \mathcal{L} & = & \sum _{\{ i: y_{i}=0\} } w_ i\ln \left[\exp (\mathbf{z}_{i}’\bgamma )+\exp (-\exp (\mathbf{x}_{i}’\bbeta )) \right] \\ & & + \sum _{\{ i: y_{i}>0\} }w_ i\left[y_{i} \mathbf{x}_{i}’\bbeta -\exp (\mathbf{x}_{i}’\bbeta ) - \sum _{k=2}^{y_{i}}\ln (k) \right] \\ & & - \sum _{i=1}^{N}w_ i\ln \left[ 1 + \exp (\mathbf{z}_{i}’\bgamma ) \right] \end{eqnarray*}

See the section Poisson Regression for the definition of $w_ i$.

The gradient for this model is given by

\[ \frac{\partial \mathcal{L}}{\partial \bgamma } = \sum _{\{ i: y_{i}=0\} } w_ i\left[\frac{\exp (\mathbf{z}_{i}'\bgamma )}{\exp (\mathbf{z}_{i}'\bgamma ) + \exp (-\exp (\mathbf{x}_{i}'\bbeta ))}\right] \mathbf{z}_{i} - \sum _{i=1}^{N}w_ i\left[\frac{\exp (\mathbf{z}_{i}'\bgamma )}{1 + \exp (\mathbf{z}_{i}'\bgamma )} \right] \mathbf{z}_{i} \]
\[ \frac{\partial \mathcal{L}}{\partial \bbeta } = \sum _{\{ i: y_{i}=0\} } w_ i\left[\frac{-\exp (\mathbf{x}_{i}'\bbeta ) \exp (-\exp (\mathbf{x}_{i}'\bbeta ))}{\exp (\mathbf{z}_{i}'\bgamma ) + \exp (-\exp (\mathbf{x}_{i}'\bbeta ))}\right] \mathbf{x}_{i} + \sum _{\{ i: y_{i}>0\} }w_ i\left[y_{i} - \exp (\mathbf{x}_{i}’\bbeta ) \right] \mathbf{x}_{i} \]

ZIP Model with Standard Normal Link Function

Next, consider the ZIP model in which the probability $\varphi _{i}$ is expressed using a standard normal link function: $\varphi _{i}= \Phi (\mathbf{z}_{i}’\bgamma )$. The log-likelihood function is

\begin{eqnarray*} \mathcal{L} & = & \sum _{\{ i: y_{i}=0\} }w_ i\ln \left\{ \Phi (\mathbf{z}_{i}’\bgamma ) + \left[ 1- \Phi (\mathbf{z}_{i}’\bgamma )\right] \exp (-\exp (\mathbf{x}_{i}’\bbeta )) \right\} \\ & + & \sum _{\{ i: y_{i}>0\} }w_ i\left\{ \ln \left[ \left( 1-\Phi (\mathbf{z}_{i}’\bgamma )\right) \right] - \exp (\mathbf{x}_{i}’\bbeta ) + y_{i} \mathbf{x}_{i}’\bbeta - \sum _{k=2}^{y_{i}} \ln (k) \right\} \end{eqnarray*}

See the section Poisson Regression for the definition of $w_ i$.

The gradient for this model is given by

\begin{eqnarray*} \frac{\partial \mathcal{L}}{\partial \bgamma } & = & \sum _{\{ i: y_{i}=0\} } w_ i\frac{\varphi (\mathbf{z}_{i}'\bgamma )\left[ 1-\exp (-\exp (\mathbf{x}_{i}'\bbeta )) \right]}{\Phi (\mathbf{z}_{i}'\bgamma ) + \left[ 1 - \Phi (\mathbf{z}_{i}'\bgamma ) \right] \exp (-\exp (\mathbf{x}_{i}'\bbeta ))} \mathbf{z}_{i} \\ & - & \sum _{\{ i: y_{i}>0\} } w_ i\frac{\varphi (\mathbf{z}_{i}'\bgamma )}{\left[ 1 - \Phi (\mathbf{z}_{i}'\bgamma ) \right]} \mathbf{z}_{i} \end{eqnarray*}
\begin{eqnarray*} \frac{\partial \mathcal{L}}{\partial \bbeta } & = & \sum _{\{ i: y_{i}=0\} } w_ i\frac{-\left[1-\Phi (\mathbf{z}_{i}'\bgamma )\right] \exp (\mathbf{x}_{i}'\bbeta ) \exp (-\exp (\mathbf{x}_{i}'\bbeta ))}{\Phi (\mathbf{z}_{i}'\bgamma ) + \left[ 1 - \Phi (\mathbf{z}_{i}'\bgamma ) \right] \exp (-\exp (\mathbf{x}_{i}'\bbeta ))} \mathbf{x}_{i} \\ & + & \sum _{\{ i: y_{i}>0\} } w_ i\left[y_{i}-\exp (\mathbf{x}_{i}’\bbeta ) \right] \mathbf{x}_{i} \end{eqnarray*}