The VARMAX Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues
Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues -
Examples

- References
RESTRICT Statement
RESTRICT restriction, …, restriction ;
The RESTRICT statement restricts the specified parameters to the specified values. Only one RESTRICT statement is allowed, but multiple restrictions can be specified in one RESTRICT statement.
The syntax for restriction is parameter=value, and each restriction is separated by commas. Parameters are referred by the following keywords:
-
CONST(
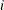 ) is the intercept parameter of the
) is the intercept parameter of the 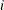 th time series
th time series 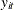
-
AR(
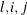 ) is the autoregressive parameter of the lag
) is the autoregressive parameter of the lag 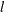 value of the
value of the 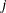 th dependent (endogenous) variable,
th dependent (endogenous) variable, 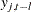 , to the
, to the 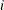 th dependent variable at time
th dependent variable at time  ,
, 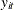
-
MA(
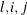 ) is the moving-average parameter of the lag
) is the moving-average parameter of the lag 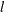 value of the
value of the 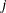 th error process,
th error process, 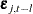 , to the
, to the 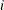 th dependent variable at time
th dependent variable at time  ,
, 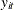
-
XL(
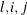 ) is the exogenous parameter of the lag
) is the exogenous parameter of the lag 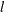 value of the
value of the 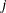 th exogenous (independent) variable,
th exogenous (independent) variable, 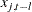 , to the
, to the 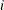 th dependent variable at time
th dependent variable at time  ,
, 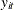
-
SDUMMY(
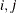 ) is the
) is the 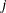 th seasonal dummy of the
th seasonal dummy of the 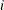 th time series at time
th time series at time  ,
, 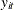 , where
, where 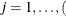 nseason
nseason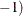 , where nseason is based on the NSEASON= option in the MODEL statement
, where nseason is based on the NSEASON= option in the MODEL statement
-
LTREND(
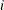 ) is the linear trend parameter of the current value
) is the linear trend parameter of the current value 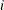 th time series
th time series 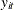
-
QTREND(
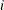 ) is the quadratic trend parameter of the current value
) is the quadratic trend parameter of the current value 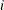 th time series
th time series 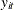
The following keywords are for the fitted GARCH model. The indexes ![]() and
and ![]() refer to the position of the element in the coefficient matrix.
refer to the position of the element in the coefficient matrix.
-
GCHC(
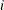 ,
,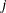 ) is the constant parameter of the covariance matrix,
) is the constant parameter of the covariance matrix, 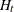 , and (
, and (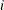 ,
,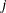 ) is
) is 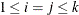 for CCC representation and
for CCC representation and 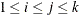 for BEKK representations, where
for BEKK representations, where 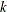 is the number of dependent variables
is the number of dependent variables
-
ACH(
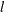 ,
,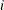 ,
,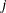 ) is the ARCH parameter of the lag
) is the ARCH parameter of the lag 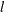 value of
value of 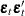 , where
, where 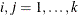 for BEKK representation and
for BEKK representation and 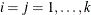 for CCC representation
for CCC representation
-
GCH(
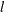 ,
,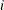 ,
,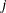 ) is the GARCH parameter of the lag
) is the GARCH parameter of the lag 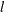 value of covariance matrix,
value of covariance matrix, 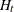 , where
, where 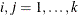 for BEKK representation and
for BEKK representation and 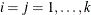 for CCC representation
for CCC representation
-
CCC(
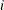 ,
,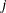 ) is the constant conditional correlation parameter for only the CCC representation; (
) is the constant conditional correlation parameter for only the CCC representation; (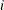 ,
,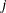 ) is
) is 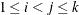
To use the RESTRICT statement, you need to know the form of the model. If the P=, Q=, and XLAG= options are not specified, then the RESTRICT statement is not applicable.
Restricted parameter estimates are computed by introducing a Lagrangian parameter for each restriction (Pringle and Rayner 1971). The Lagrangian parameter measures the sensitivity of the sum of square errors to the restriction. The estimates of these Lagrangian parameters and their significance are printed in the restriction results table.
The following are examples of the RESTRICT statement. The first example shows a bivariate (![]() =2) VAR(2) model,
=2) VAR(2) model,
proc varmax data=one;
model y1 y2 / p=2;
restrict AR(1,1,2)=0, AR(2,1,2)=0.3;
run;
The AR(1,1,2) and AR(2,1,2) parameters are fixed as AR(1,1,2)=0 and AR(2,1,2)=0.3, respectively, and other parameters are to be estimated.
The following shows a bivariate (![]() =2) VARX(1,1) model with three exogenous variables,
=2) VARX(1,1) model with three exogenous variables,
proc varmax data=two;
model y1 = x1 x2, y2 = x2 x3 / p=1 xlag=1;
restrict XL(0,1,1)=-1.2, XL(1,2,3)=0;
run;
The XL(0,1,1) and XL(1,2,3) parameters are fixed as XL(0,1,1)=–1.2 and XL(1,2,3)=0, respectively, and other parameters are to be estimated.