The VARMAX Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues
Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues -
Examples

- References
Vector Error Correction Modeling
This section discusses the implication of cointegration for the autoregressive representation. Assume that the cointegrated series can be represented by a vector error correction model according to the Granger representation theorem (Engle and Granger 1987). Consider the vector autoregressive process with Gaussian errors defined by
|
|
or
|
|
where the initial values, ![]() , are fixed and
, are fixed and ![]() . Since the AR operator
. Since the AR operator ![]() can be re-expressed as
can be re-expressed as ![]() , where
, where ![]() with
with ![]() , the vector error correction model is
, the vector error correction model is
|
|
or
|
|
where ![]() .
.
One motivation for the VECM(![]() ) form is to consider the relation
) form is to consider the relation ![]() as defining the underlying economic relations and assume that the agents react to the disequilibrium error
as defining the underlying economic relations and assume that the agents react to the disequilibrium error ![]() through the adjustment coefficient
through the adjustment coefficient ![]() to restore equilibrium; that is, they satisfy the economic relations. The cointegrating vector,
to restore equilibrium; that is, they satisfy the economic relations. The cointegrating vector, ![]() is sometimes called the long-run parameters.
is sometimes called the long-run parameters.
You can consider a vector error correction model with a deterministic term. The deterministic term ![]() can contain a constant, a linear trend, and seasonal dummy variables. Exogenous variables can also be included in the model.
can contain a constant, a linear trend, and seasonal dummy variables. Exogenous variables can also be included in the model.
|
|
where ![]() .
.
The alternative vector error correction representation considers the error correction term at lag ![]() and is written as
and is written as
|
|
If the matrix ![]() has a full-rank (
has a full-rank (![]() ), all components of
), all components of ![]() are
are ![]() . On the other hand,
. On the other hand, ![]() are stationary in difference if
are stationary in difference if ![]() . When the rank of the matrix
. When the rank of the matrix ![]() is
is ![]() , there are
, there are ![]() linear combinations that are nonstationary and
linear combinations that are nonstationary and ![]() stationary cointegrating relations. Note that the linearly independent vector
stationary cointegrating relations. Note that the linearly independent vector ![]() is stationary and this transformation is not unique unless
is stationary and this transformation is not unique unless ![]() . There does not exist a unique cointegrating matrix
. There does not exist a unique cointegrating matrix ![]() since the coefficient matrix
since the coefficient matrix ![]() can also be decomposed as
can also be decomposed as
|
|
where ![]() is an
is an ![]() nonsingular matrix.
nonsingular matrix.
Test for the Cointegration
The cointegration rank test determines the linearly independent columns of ![]() . Johansen (1988, 1995a) and Johansen and Juselius (1990) proposed the cointegration rank test by using the reduced rank regression.
. Johansen (1988, 1995a) and Johansen and Juselius (1990) proposed the cointegration rank test by using the reduced rank regression.
Different Specifications of Deterministic Trends
When you construct the VECM(![]() ) form from the VAR(
) form from the VAR(![]() ) model, the deterministic terms in the VECM(
) model, the deterministic terms in the VECM(![]() ) form can differ from those in the VAR(
) form can differ from those in the VAR(![]() ) model. When there are deterministic cointegrated relationships among variables, deterministic terms in the VAR(
) model. When there are deterministic cointegrated relationships among variables, deterministic terms in the VAR(![]() ) model are not present in the VECM(
) model are not present in the VECM(![]() ) form. On the other hand, if there are stochastic cointegrated relationships in the VAR(
) form. On the other hand, if there are stochastic cointegrated relationships in the VAR(![]() ) model, deterministic terms appear in the VECM(
) model, deterministic terms appear in the VECM(![]() ) form via the error correction term or as an independent term in the VECM(
) form via the error correction term or as an independent term in the VECM(![]() ) form. There are five different specifications of deterministic trends in the VECM(
) form. There are five different specifications of deterministic trends in the VECM(![]() ) form.
) form.
-
Case 1: There is no separate drift in the VECM(
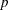 ) form.
) form.
![\[ \Delta \mb {y} _ t = \balpha \bbeta ’\mb {y} _{t-1} + \sum _{i=1}^{p-1} \Phi ^*_ i \Delta \mb {y} _{t-i} +\bepsilon _ t \]](images/etsug_varmax0855.png)
-
Case 2: There is no separate drift in the VECM(
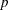 ) form, but a constant enters only via the error correction term.
) form, but a constant enters only via the error correction term.
![\[ \Delta \mb {y} _ t = \balpha (\bbeta ’, \beta _0)(\mb {y} _{t-1}’,1)’ + \sum _{i=1}^{p-1} \Phi ^*_ i \Delta \mb {y} _{t-i} + \bepsilon _ t \]](images/etsug_varmax0232.png)
-
Case 3: There is a separate drift and no separate linear trend in the VECM(
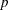 ) form.
) form.
![\[ \Delta \mb {y} _ t = \balpha \bbeta ’\mb {y} _{t-1} + \sum _{i=1}^{p-1} \Phi ^*_ i \Delta \mb {y} _{t-i} + \bdelta _0 + \bepsilon _ t \]](images/etsug_varmax0856.png)
-
Case 4: There is a separate drift and no separate linear trend in the VECM(
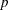 ) form, but a linear trend enters only via the error correction term.
) form, but a linear trend enters only via the error correction term.
![\[ \Delta \mb {y} _ t = \balpha (\bbeta ’, \beta _1)(\mb {y} _{t-1}’,t)’ + \sum _{i=1}^{p-1} \Phi ^*_ i \Delta \mb {y} _{t-i} + \bdelta _0 + \bepsilon _ t \]](images/etsug_varmax0233.png)
-
Case 5: There is a separate linear trend in the VECM(
 ) form.
) form.
![\[ \Delta \mb {y} _ t = \balpha \bbeta ’\mb {y} _{t-1} + \sum _{i=1}^{p-1} \Phi ^*_ i \Delta \mb {y} _{t-i} + \bdelta _0 + \bdelta _1t + \bepsilon _ t \]](images/etsug_varmax0857.png)
First, focus on Cases 1, 3, and 5 to test the null hypothesis that there are at most ![]() cointegrating vectors. Let
cointegrating vectors. Let
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
where ![]() can be empty for Case 1, 1 for Case 3, and
can be empty for Case 1, 1 for Case 3, and ![]() for Case 5.
for Case 5.
In Case 2, ![]() and
and ![]() are defined as
are defined as
|
|
|
|
|
|
|
|
In Case 4, ![]() and
and ![]() are defined as
are defined as
|
|
|
|
|
|
|
|
Let ![]() be the matrix of parameters consisting of
be the matrix of parameters consisting of ![]() , …,
, …, ![]() ,
, ![]() , and
, and ![]() , …,
, …, ![]() , where parameters
, where parameters ![]() corresponds to regressors
corresponds to regressors ![]() . Then the VECM(
. Then the VECM(![]() ) form is rewritten in these variables as
) form is rewritten in these variables as
|
|
The log-likelihood function is given by
|
|
|
|
|
|
|
|
The residuals, ![]() and
and ![]() , are obtained by regressing
, are obtained by regressing ![]() and
and ![]() on
on ![]() , respectively. The regression equation of residuals is
, respectively. The regression equation of residuals is
|
|
The crossproducts matrices are computed
|
|
Then the maximum likelihood estimator for ![]() is obtained from the eigenvectors that correspond to the
is obtained from the eigenvectors that correspond to the ![]() largest eigenvalues of the following equation:
largest eigenvalues of the following equation:
|
|
The eigenvalues of the preceding equation are squared canonical correlations between ![]() and
and ![]() , and the eigenvectors that correspond to the
, and the eigenvectors that correspond to the ![]() largest eigenvalues are the
largest eigenvalues are the ![]() linear combinations of
linear combinations of ![]() , which have the largest squared partial correlations with the stationary process
, which have the largest squared partial correlations with the stationary process ![]() after correcting for lags and deterministic terms. Such an analysis calls for a reduced rank regression of
after correcting for lags and deterministic terms. Such an analysis calls for a reduced rank regression of ![]() on
on ![]() corrected for
corrected for ![]() , as discussed by Anderson (1951). Johansen (1988) suggests two test statistics to test the null hypothesis that there are
at most
, as discussed by Anderson (1951). Johansen (1988) suggests two test statistics to test the null hypothesis that there are
at most ![]() cointegrating vectors
cointegrating vectors
|
|
Trace Test
The trace statistic for testing the null hypothesis that there are at most ![]() cointegrating vectors is as follows:
cointegrating vectors is as follows:
|
|
The asymptotic distribution of this statistic is given by
|
|
where ![]() is the trace of a matrix
is the trace of a matrix ![]() ,
, ![]() is the
is the ![]() dimensional Brownian motion, and
dimensional Brownian motion, and ![]() is the Brownian motion itself, or the demeaned or detrended Brownian motion according to the different specifications of
deterministic trends in the vector error correction model.
is the Brownian motion itself, or the demeaned or detrended Brownian motion according to the different specifications of
deterministic trends in the vector error correction model.
Maximum Eigenvalue Test
The maximum eigenvalue statistic for testing the null hypothesis that there are at most ![]() cointegrating vectors is as follows:
cointegrating vectors is as follows:
|
|
The asymptotic distribution of this statistic is given by
|
|
where ![]() is the maximum eigenvalue of a matrix
is the maximum eigenvalue of a matrix ![]() . Osterwald-Lenum (1992) provided detailed tables of the critical values of these statistics.
. Osterwald-Lenum (1992) provided detailed tables of the critical values of these statistics.
The following statements use the JOHANSEN option to compute the Johansen cointegration rank trace test of integrated order 1:
proc varmax data=simul2; model y1 y2 / p=2 cointtest=(johansen=(normalize=y1)); run;
Figure 36.52 shows the output based on the model specified in the MODEL statement, an intercept term is assumed. In the “Cointegration Rank Test Using Trace” table, the column Drift In ECM means there is no separate drift in the error correction model and the column Drift In Process means the process has a constant drift before differencing. The “Cointegration Rank Test Using Trace” table shows the trace statistics based on Case 3 and the “Cointegration Rank Test Using Trace under Restriction” table shows the trace statistics based on Case 2. The output indicates that the series are cointegrated with rank 1 because the trace statistics are smaller than the critical values in both Case 2 and Case 3.
Figure 36.52: Cointegration Rank Test (COINTTEST=(JOHANSEN=) Option)
| Cointegration Rank Test Using Trace | ||||||
|---|---|---|---|---|---|---|
| H0: Rank=r |
H1: Rank>r |
Eigenvalue | Trace | 5% Critical Value | Drift in ECM | Drift in Process |
| 0 | 0 | 0.4644 | 61.7522 | 15.34 | Constant | Linear |
| 1 | 1 | 0.0056 | 0.5552 | 3.84 | ||
| Cointegration Rank Test Using Trace Under Restriction | ||||||
|---|---|---|---|---|---|---|
| H0: Rank=r |
H1: Rank>r |
Eigenvalue | Trace | 5% Critical Value | Drift in ECM | Drift in Process |
| 0 | 0 | 0.5209 | 76.3788 | 19.99 | Constant | Constant |
| 1 | 1 | 0.0426 | 4.2680 | 9.13 | ||
Figure 36.53 shows which result, either Case 2 (the hypothesis H0) or Case 3 (the hypothesis H1), is appropriate depending on the significance
level. Since the cointegration rank is chosen to be 1 by the result in Figure 36.52, look at the last row that corresponds to rank=1. Since the ![]() -value is 0.054, the Case 2 cannot be rejected at the significance level 5%, but it can be rejected at the significance level
10%. For modeling of the two Case 2 and Case 3, see Figure 36.56 and Figure 36.57.
-value is 0.054, the Case 2 cannot be rejected at the significance level 5%, but it can be rejected at the significance level
10%. For modeling of the two Case 2 and Case 3, see Figure 36.56 and Figure 36.57.
Figure 36.53: Cointegration Rank Test Continued
| Hypothesis of the Restriction | ||
|---|---|---|
| Hypothesis | Drift in ECM | Drift in Process |
| H0(Case 2) | Constant | Constant |
| H1(Case 3) | Constant | Linear |
| Hypothesis Test of the Restriction | |||||
|---|---|---|---|---|---|
| Rank | Eigenvalue | Restricted Eigenvalue |
DF | Chi-Square | Pr > ChiSq |
| 0 | 0.4644 | 0.5209 | 2 | 14.63 | 0.0007 |
| 1 | 0.0056 | 0.0426 | 1 | 3.71 | 0.0540 |
Figure 36.54 shows the estimates of long-run parameter (Beta) and adjustment coefficients (Alpha) based on Case 3.
Figure 36.54: Cointegration Rank Test Continued
| Beta | ||
|---|---|---|
| Variable | 1 | 2 |
| y1 | 1.00000 | 1.00000 |
| y2 | -2.04869 | -0.02854 |
| Alpha | ||
|---|---|---|
| Variable | 1 | 2 |
| y1 | -0.46421 | -0.00502 |
| y2 | 0.17535 | -0.01275 |
Using the NORMALIZE= option, the first low of the “Beta” table has 1. Considering that the cointegration rank is 1, the long-run relationship of the series is
|
|
|
|
|
|
|
|
|
|
|
|
Figure 36.55 shows the estimates of long-run parameter (Beta) and adjustment coefficients (Alpha) based on Case 2.
Figure 36.55: Cointegration Rank Test Continued
| Beta Under Restriction | ||
|---|---|---|
| Variable | 1 | 2 |
| y1 | 1.00000 | 1.00000 |
| y2 | -2.04366 | -2.75773 |
| 1 | 6.75919 | 101.37051 |
| Alpha Under Restriction | ||
|---|---|---|
| Variable | 1 | 2 |
| y1 | -0.48015 | 0.01091 |
| y2 | 0.12538 | 0.03722 |
Considering that the cointegration rank is 1, the long-run relationship of the series is
|
|
|
![$\displaystyle \left[ \begin{array}{rrr} 1 & -2.04366 & 6.75919 \\ \end{array} \right] \left[ \begin{array}{r} y_1 \\ y_2 \\ 1 \end{array} \right] $](images/etsug_varmax0914.png) |
|
|
|
|
|
|
|
|
Estimation of Vector Error Correction Model
The preceding log-likelihood function is maximized for
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The estimators of the orthogonal complements of ![]() and
and ![]() are
are
|
|
and
|
|
The ML estimators have the following asymptotic properties:
|
|
where
|
|
and
|
|
The following statements are examples of fitting the five different cases of the vector error correction models mentioned in the previous section.
For fitting Case 1,
model y1 y2 / p=2 ecm=(rank=1 normalize=y1) noint;
For fitting Case 2,
model y1 y2 / p=2 ecm=(rank=1 normalize=y1 ectrend);
For fitting Case 3,
model y1 y2 / p=2 ecm=(rank=1 normalize=y1);
model y1 y2 / p=2 ecm=(rank=1 normalize=y1 ectrend)
trend=linear;
For fitting Case 5,
model y1 y2 / p=2 ecm=(rank=1 normalize=y1) trend=linear;
From Figure 36.53 that uses the COINTTEST=(JOHANSEN) option, you can fit the model by using either Case 2 or Case 3 because the test was not significant at the 0.05 level, but was significant at the 0.10 level. Here both models are fitted to show the difference in output display. Figure 36.56 is for Case 2, and Figure 36.57 is for Case 3.
For Case 2,
proc varmax data=simul2;
model y1 y2 / p=2 ecm=(rank=1 normalize=y1 ectrend)
print=(estimates);
run;
Figure 36.56: Parameter Estimation with the ECTREND Option
| Parameter Alpha * Beta' Estimates | |||
|---|---|---|---|
| Variable | y1 | y2 | 1 |
| y1 | -0.48015 | 0.98126 | -3.24543 |
| y2 | 0.12538 | -0.25624 | 0.84748 |
| AR Coefficients of Differenced Lag | |||
|---|---|---|---|
| DIF Lag | Variable | y1 | y2 |
| 1 | y1 | -0.72759 | -0.77463 |
| y2 | 0.38982 | -0.55173 | |
| Model Parameter Estimates | ||||||
|---|---|---|---|---|---|---|
| Equation | Parameter | Estimate | Standard Error |
t Value | Pr > |t| | Variable |
| D_y1 | CONST1 | -3.24543 | 0.33022 | 1, EC | ||
| AR1_1_1 | -0.48015 | 0.04886 | y1(t-1) | |||
| AR1_1_2 | 0.98126 | 0.09984 | y2(t-1) | |||
| AR2_1_1 | -0.72759 | 0.04623 | -15.74 | 0.0001 | D_y1(t-1) | |
| AR2_1_2 | -0.77463 | 0.04978 | -15.56 | 0.0001 | D_y2(t-1) | |
| D_y2 | CONST2 | 0.84748 | 0.35394 | 1, EC | ||
| AR1_2_1 | 0.12538 | 0.05236 | y1(t-1) | |||
| AR1_2_2 | -0.25624 | 0.10702 | y2(t-1) | |||
| AR2_2_1 | 0.38982 | 0.04955 | 7.87 | 0.0001 | D_y1(t-1) | |
| AR2_2_2 | -0.55173 | 0.05336 | -10.34 | 0.0001 | D_y2(t-1) | |
Figure 36.56 can be reported as follows:
|
|
|
![$\displaystyle \left[ \begin{array}{rrr} -0.48015 & 0.98126 & -3.24543 \\ 0.12538 & -0.25624& 0.84748 \end{array} \right] \left[ \begin{array}{c} y_{1,t-1} \\ y_{2,t-1} \\ 1 \end{array} \right] $](images/etsug_varmax0938.png) |
|
|
|
|
The keyword “EC” in the “Model Parameter Estimates” table means that the ECTREND option is used for fitting the model.
For fitting Case 3,
proc varmax data=simul2;
model y1 y2 / p=2 ecm=(rank=1 normalize=y1)
print=(estimates);
run;
Figure 36.57: Parameter Estimation without the ECTREND Option
| Parameter Alpha * Beta' Estimates | ||
|---|---|---|
| Variable | y1 | y2 |
| y1 | -0.46421 | 0.95103 |
| y2 | 0.17535 | -0.35923 |
| AR Coefficients of Differenced Lag | |||
|---|---|---|---|
| DIF Lag | Variable | y1 | y2 |
| 1 | y1 | -0.74052 | -0.76305 |
| y2 | 0.34820 | -0.51194 | |
| Model Parameter Estimates | ||||||
|---|---|---|---|---|---|---|
| Equation | Parameter | Estimate | Standard Error |
t Value | Pr > |t| | Variable |
| D_y1 | CONST1 | -2.60825 | 1.32398 | -1.97 | 0.0518 | 1 |
| AR1_1_1 | -0.46421 | 0.05474 | y1(t-1) | |||
| AR1_1_2 | 0.95103 | 0.11215 | y2(t-1) | |||
| AR2_1_1 | -0.74052 | 0.05060 | -14.63 | 0.0001 | D_y1(t-1) | |
| AR2_1_2 | -0.76305 | 0.05352 | -14.26 | 0.0001 | D_y2(t-1) | |
| D_y2 | CONST2 | 3.43005 | 1.39587 | 2.46 | 0.0159 | 1 |
| AR1_2_1 | 0.17535 | 0.05771 | y1(t-1) | |||
| AR1_2_2 | -0.35923 | 0.11824 | y2(t-1) | |||
| AR2_2_1 | 0.34820 | 0.05335 | 6.53 | 0.0001 | D_y1(t-1) | |
| AR2_2_2 | -0.51194 | 0.05643 | -9.07 | 0.0001 | D_y2(t-1) | |
Figure 36.57 can be reported as follows:
|
|
|
|
|
|
|
|
Test for the Linear Restriction on the Parameters
Consider the example with the variables ![]() log real money,
log real money, ![]() log real income,
log real income, ![]() deposit interest rate, and
deposit interest rate, and ![]() bond interest rate. It seems a natural hypothesis that in the long-run relation, money and income have equal coefficients
with opposite signs. This can be formulated as the hypothesis that the cointegrated relation contains only
bond interest rate. It seems a natural hypothesis that in the long-run relation, money and income have equal coefficients
with opposite signs. This can be formulated as the hypothesis that the cointegrated relation contains only ![]() and
and ![]() through
through ![]() . For the analysis, you can express these restrictions in the parameterization of
. For the analysis, you can express these restrictions in the parameterization of ![]() such that
such that ![]() , where
, where ![]() is a known
is a known ![]() matrix and
matrix and ![]() is the
is the ![]() parameter matrix to be estimated. For this example,
parameter matrix to be estimated. For this example, ![]() is given by
is given by
![\[ H = \left[ \begin{array}{rrr} 1 & 0 & 0 \\ -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right] \]](images/etsug_varmax0949.png) |
Restriction ![]()
When the linear restriction ![]() is given, it implies that the same restrictions are imposed on all cointegrating vectors. You obtain the maximum likelihood
estimator of
is given, it implies that the same restrictions are imposed on all cointegrating vectors. You obtain the maximum likelihood
estimator of ![]() by reduced rank regression of
by reduced rank regression of ![]() on
on ![]() corrected for
corrected for ![]() , solving the following equation
, solving the following equation
|
|
for the eigenvalues ![]() and eigenvectors
and eigenvectors ![]() ,
, ![]() given in the preceding section. Then choose
given in the preceding section. Then choose ![]() that corresponds to the
that corresponds to the ![]() largest eigenvalues, and the
largest eigenvalues, and the ![]() is
is ![]() .
.
The test statistic for ![]() is given by
is given by
|
|
If the series has no deterministic trend, the constant term should be restricted by ![]() as in Case 2. Then
as in Case 2. Then ![]() is given by
is given by
![\[ H = \left[ \begin{array}{rrrr} 1 & 0 & 0 & 0\\ -1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{array} \right] \]](images/etsug_varmax0962.png) |
The following statements test that 2 ![]() :
:
proc varmax data=simul2; model y1 y2 / p=2 ecm=(rank=1 normalize=y1); cointeg rank=1 h=(1,-2); run;
Figure 36.58 shows the results of testing ![]() . The input
. The input ![]() matrix is
matrix is ![]() . The adjustment coefficient is reestimated under the restriction, and the test indicates that you cannot reject the null
hypothesis.
. The adjustment coefficient is reestimated under the restriction, and the test indicates that you cannot reject the null
hypothesis.
Figure 36.58: Testing of Linear Restriction (H= Option)
| Beta Under Restriction | |
|---|---|
| Variable | 1 |
| y1 | 1.00000 |
| y2 | -2.00000 |
| Alpha Under Restriction | |
|---|---|
| Variable | 1 |
| y1 | -0.47404 |
| y2 | 0.17534 |
| Hypothesis Test | |||||
|---|---|---|---|---|---|
| Index | Eigenvalue | Restricted Eigenvalue |
DF | Chi-Square | Pr > ChiSq |
| 1 | 0.4644 | 0.4616 | 1 | 0.51 | 0.4738 |
Test for the Weak Exogeneity and Restrictions of Alpha
Consider a vector error correction model:
|
|
Divide the process ![]() into
into ![]() with dimension
with dimension ![]() and
and ![]() and the
and the ![]() into
into
|
|
Similarly, the parameters can be decomposed as follows:
|
|
Then the VECM(p) form can be rewritten by using the decomposed parameters and processes:
|
|
The conditional model for ![]() given
given ![]() is
is
|
|
|
|
|
|
|
|
and the marginal model of ![]() is
is
|
|
where ![]() .
.
The test of weak exogeneity of ![]() for the parameters
for the parameters ![]() determines whether
determines whether ![]() . Weak exogeneity means that there is no information about
. Weak exogeneity means that there is no information about ![]() in the marginal model or that the variables
in the marginal model or that the variables ![]() do not react to a disequilibrium.
do not react to a disequilibrium.
Restriction ![]()
Consider the null hypothesis ![]() , where
, where ![]() is a
is a ![]() matrix with
matrix with ![]() .
.
From the previous residual regression equation
|
|
you can obtain
|
|
|
|
|
|
|
|
where ![]() and
and ![]() is orthogonal to
is orthogonal to ![]() such that
such that ![]() .
.
Define
|
|
and let ![]() . Then
. Then ![]() can be written as
can be written as
|
|
Using the marginal distribution of ![]() and the conditional distribution of
and the conditional distribution of ![]() , the new residuals are computed as
, the new residuals are computed as
|
|
|
|
|
|
|
|
where
|
|
In terms of ![]() and
and ![]() , the MLE of
, the MLE of ![]() is computed by using the reduced rank regression. Let
is computed by using the reduced rank regression. Let
|
|
Under the null hypothesis ![]() , the MLE
, the MLE ![]() is computed by solving the equation
is computed by solving the equation
|
|
Then ![]() , where the eigenvectors correspond to the
, where the eigenvectors correspond to the ![]() largest eigenvalues and are normalized such that
largest eigenvalues and are normalized such that ![]() ;
; ![]() . The likelihood ratio test for
. The likelihood ratio test for ![]() is
is
|
|
See Theorem 6.1 in Johansen and Juselius (1990) for more details.
The test of weak exogeneity of ![]() is a special case of the test
is a special case of the test ![]() , considering
, considering ![]() . Consider the previous example with four variables (
. Consider the previous example with four variables ( ![]() ). If
). If ![]() , you formulate the weak exogeneity of (
, you formulate the weak exogeneity of (![]() ) for
) for ![]() as
as ![]() and the weak exogeneity of
and the weak exogeneity of ![]() for (
for (![]() ) as
) as ![]() .
.
The following statements test the weak exogeneity of other variables, assuming ![]() :
:
proc varmax data=simul2; model y1 y2 / p=2 ecm=(rank=1 normalize=y1); cointeg rank=1 exogeneity; run;
proc varmax data=simul2; model y1 y2 / p=2 ecm=(rank=1 normalize=y1); cointeg rank=1 j=exogeneity; run;
Figure 36.59 shows that each variable is not the weak exogeneity of other variable.
Figure 36.59: Testing of Weak Exogeneity (EXOGENEITY Option)
| Testing Weak Exogeneity of Each Variables |
|||
|---|---|---|---|
| Variable | DF | Chi-Square | Pr > ChiSq |
| y1 | 1 | 53.46 | <.0001 |
| y2 | 1 | 8.76 | 0.0031 |
Forecasting of the VECM
Consider the cointegrated moving-average representation of the differenced process of ![]()
|
|
Assume that ![]() . The linear process
. The linear process ![]() can be written as
can be written as
|
|
Therefore, for any ![]() ,
,
|
|
The ![]() -step-ahead forecast is derived from the preceding equation:
-step-ahead forecast is derived from the preceding equation:
|
|
Note that
|
|
since ![]() and
and ![]() . The long-run forecast of the cointegrated system shows that the cointegrated relationship holds, although there might exist
some deviations from the equilibrium status in the short-run. The covariance matrix of the predict error
. The long-run forecast of the cointegrated system shows that the cointegrated relationship holds, although there might exist
some deviations from the equilibrium status in the short-run. The covariance matrix of the predict error ![]() is
is
|
|
When the linear process is represented as a VECM(![]() ) model, you can obtain
) model, you can obtain
|
|
The transition equation is defined as
|
|
where ![]() is a state vector and the transition matrix is
is a state vector and the transition matrix is
![$\displaystyle F = \left[ \begin{array}{cccccc} I_ k & I_ k & 0 & \cdots & 0 \\ \Pi & (\Pi +\Phi ^*_1)& \Phi ^*_2 & \cdots & \Phi ^*_{p-1} \\ 0 & I_ k & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & I_ k & 0 \\ \end{array} \right] $](images/etsug_varmax1043.png) |
where 0 is a ![]() zero matrix. The observation equation can be written
zero matrix. The observation equation can be written
|
|
where ![]() .
.
The ![]() -step-ahead forecast is computed as
-step-ahead forecast is computed as
|
|
Cointegration with Exogenous Variables
The error correction model with exogenous variables can be written as follows:
|
|
The following statements demonstrate how to fit VECMX(![]() ), where
), where ![]() and
and ![]() from the P=2 and XLAG=1 options:
from the P=2 and XLAG=1 options:
proc varmax data=simul3;
model y1 y2 = x1 / p=2 xlag=1 ecm=(rank=1);
run;
The following statements demonstrate how to BVECMX(2,1):
proc varmax data=simul3;
model y1 y2 = x1 / p=2 xlag=1 ecm=(rank=1)
prior=(lambda=0.9 theta=0.1);
run;