The VARMAX Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues
Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues -
Examples

- References
VARMAX Model
The vector autoregressive moving-average model with exogenous variables is called the VARMAX(![]() ,
,![]() ,
,![]() ) model. The form of the model can be written as
) model. The form of the model can be written as
|
|
where the output variables of interest, ![]() , can be influenced by other input variables,
, can be influenced by other input variables, ![]() , which are determined outside of the system of interest. The variables
, which are determined outside of the system of interest. The variables ![]() are referred to as dependent, response, or endogenous variables, and the variables
are referred to as dependent, response, or endogenous variables, and the variables ![]() are referred to as independent, input, predictor, regressor, or exogenous variables. The unobserved noise variables,
are referred to as independent, input, predictor, regressor, or exogenous variables. The unobserved noise variables, ![]() , are a vector white noise process.
, are a vector white noise process.
The VARMAX(![]() ,
,![]() ,
,![]() ) model can be written
) model can be written
|
|
|
|
where
|
|
|
|
|
|
|
|
|
|
|
|
are matrix polynomials in ![]() in the backshift operator, such that
in the backshift operator, such that ![]() , the
, the ![]() and
and ![]() are
are ![]() matrices, and the
matrices, and the ![]() are
are ![]() matrices.
matrices.
The following assumptions are made:
-
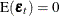 ,
, 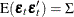 , which is positive-definite, and
, which is positive-definite, and 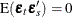 for
for 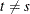 .
.
-
For stationarity and invertibility of the VARMAX process, the roots of
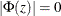 and
and 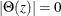 are outside the unit circle.
are outside the unit circle.
-
The exogenous (independent) variables
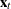 are not correlated with residuals
are not correlated with residuals 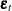 ,
, 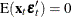 . The exogenous variables can be stochastic or nonstochastic. When the exogenous variables are stochastic and their future
values are unknown, forecasts of these future values are needed to forecast the future values of the endogenous (dependent)
variables. On occasion, future values of the exogenous variables can be assumed to be known because they are deterministic
variables. The VARMAX procedure assumes that the exogenous variables are nonstochastic if future values are available in the
input data set. Otherwise, the exogenous variables are assumed to be stochastic and their future values are forecasted by
assuming that they follow the VARMA(
. The exogenous variables can be stochastic or nonstochastic. When the exogenous variables are stochastic and their future
values are unknown, forecasts of these future values are needed to forecast the future values of the endogenous (dependent)
variables. On occasion, future values of the exogenous variables can be assumed to be known because they are deterministic
variables. The VARMAX procedure assumes that the exogenous variables are nonstochastic if future values are available in the
input data set. Otherwise, the exogenous variables are assumed to be stochastic and their future values are forecasted by
assuming that they follow the VARMA(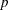 ,
,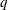 ) model, prior to forecasting the endogenous variables, where
) model, prior to forecasting the endogenous variables, where 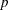 and
and 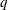 are the same as in the VARMAX(
are the same as in the VARMAX(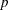 ,
,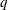 ,
, ) model.
) model.
State-Space Representation
Another representation of the VARMAX(![]() ,
,![]() ,
,![]() ) model is in the form of a state-variable or a state-space model, which consists of a state equation
) model is in the form of a state-variable or a state-space model, which consists of a state equation
|
|
and an observation equation
|
|
where
![\[ \mb {z} _{t} = \left[\begin{matrix} \mb {y} _{t} \\ \vdots \\ \mb {y} _{t-p+1} \\ \mb {x} _{t} \\ \vdots \\ \mb {x} _{t-s+1} \\ \bepsilon _{t} \\ \vdots \\ \bepsilon _{t-q+1} \end{matrix}\right], ~ ~ K = \left[\begin{matrix} \Theta ^*_0 \\ 0_{k\times r} \\ \vdots \\ 0_{k\times r} \\ I_ r \\ 0_{r\times r} \\ \vdots \\ 0_{r\times r} \\ 0_{k\times r} \\ \vdots \\ 0_{k\times r} \end{matrix}\right], ~ ~ G = \left[\begin{matrix} I_ k \\ 0_{k\times k} \\ \vdots \\ 0_{k\times k} \\ 0_{r\times k} \\ \vdots \\ 0_{r\times k} \\ I_{k\times k} \\ 0_{k\times k} \\ \vdots \\ 0_{k\times k} \end{matrix}\right] \]](images/etsug_varmax0273.png) |
![\[ F = \left[\begin{matrix} \Phi _{1} & \cdots & \Phi _{p-1} & \Phi _{p} & \Theta ^*_{1} & \cdots & \Theta ^*_{s-1} & \Theta ^*_{s} & -\Theta _{1} & \cdots & -\Theta _{q-1} & -\Theta _{q} \\ I_ k & \cdots & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & \cdots & I_ k & 0 & 0 & \cdots & 0 & 0 & 0 & \cdots & 0 & 0 \\ 0 & \cdots & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & \cdots & 0 & 0 \\ 0 & \cdots & 0 & 0 & I_ r & \cdots & 0 & 0 & 0 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & \cdots & 0 & 0 & 0 & \cdots & I_ r & 0 & 0 & \cdots & 0 & 0 \\ 0 & \cdots & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & \cdots & 0 & 0 \\ 0 & \cdots & 0 & 0 & 0 & \cdots & 0 & 0 & I_ k & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & \cdots & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & \cdots & I_ k & 0 \end{matrix} \right] \]](images/etsug_varmax0274.png) |
and
|
|
On the other hand, it is assumed that ![]() follows a VARMA(
follows a VARMA(![]() ,
,![]() ) model
) model
|
|
The model can also be expressed as
|
|
where ![]() and
and ![]() are matrix polynomials in
are matrix polynomials in ![]() , and the
, and the ![]() and
and ![]() are
are ![]() matrices. Without loss of generality, the AR and MA orders can be taken to be the same as the VARMAX(
matrices. Without loss of generality, the AR and MA orders can be taken to be the same as the VARMAX(![]() ,
,![]() ,
,![]() ) model, and
) model, and ![]() and
and ![]() are independent white noise processes.
are independent white noise processes.
Under suitable conditions such as stationarity, ![]() is represented by an infinite order moving-average process
is represented by an infinite order moving-average process
|
|
where ![]() .
.
The optimal minimum mean squared error (minimum MSE) ![]() -step-ahead forecast of
-step-ahead forecast of ![]() is
is
|
|
|
|
|
|
|
|
For ![]() ,
,
|
|
The VARMAX(![]() ,
,![]() ,
,![]() ) model has an absolutely convergent representation as
) model has an absolutely convergent representation as
|
|
|
|
|
|
|
|
|
|
|
|
or
|
|
where ![]() ,
, ![]() , and
, and ![]() .
.
The optimal (minimum MSE) ![]() -step-ahead forecast of
-step-ahead forecast of ![]() is
is
|
|
|
|
|
|
|
|
for ![]() with
with ![]() . For
. For ![]() ,
,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
where ![]() .
.
Define ![]() . For
. For ![]() with
with ![]() , you obtain
, you obtain
|
|
|
|
|
|
|
|
From the preceding relations, a state equation is
|
|
and an observation equation is
|
|
where
![\[ \mb {z} _{t} = \left[\begin{matrix} \mb {y} _{t} \\ \mb {y} _{t+1|t} \\ {\vdots } \\ \mb {y} _{t+v-1|t} \\ \mb {x} _{t} \\ \mb {x} _{t+1|t} \\ {\vdots } \\ \mb {x} _{t+v-1|t} \end{matrix}\right], ~ ~ \mb {x} _{t}^* = \left[\begin{matrix} \mb {x} _{t+v-u} \\ \mb {x} _{t+v-u+1} \\ {\vdots } \\ \mb {x} _{t-1} \end{matrix}\right], ~ ~ \mb {e} _{t+1} = \left[\begin{matrix} \mb {a} _{t+1} \\ \bepsilon _{t+1} \end{matrix}\right] \]](images/etsug_varmax0327.png) |
![\[ F = \left[\begin{matrix} 0 & I_ k & 0 & {\cdots } & 0 & 0 & 0 & 0 & {\cdots } & 0 \\ 0 & 0 & I_ k & {\cdots } & 0 & 0 & 0 & 0 & {\cdots } & 0 \\ {\vdots } & {\vdots } & {\vdots } & \ddots & {\vdots } & {\vdots } & {\vdots } & {\vdots } & \ddots & {\vdots } \\ \Phi _{v} & \Phi _{v-1} & \Phi _{v-2} & {\cdots } & \Phi _{1} & \Pi _{v} & \Pi _{v-1} & \Pi _{v-2} & {\cdots } & \Pi _{1} \\ 0 & 0 & 0 & {\cdots } & 0 & 0 & I_ r & 0 & {\cdots } & 0 \\ 0 & 0 & 0 & {\cdots } & 0 & 0 & 0 & I_ r & {\cdots } & 0 \\ {\vdots } & {\vdots } & {\vdots } & \ddots & {\vdots } & {\vdots } & {\vdots } & {\vdots } & \ddots & {\vdots } \\ 0 & 0 & 0 & {\cdots } & 0 & A_ v & A_{v-1} & A_{v-2} & {\cdots } & A_1 \\ \end{matrix} \right] \]](images/etsug_varmax0328.png) |
![\[ K = \left[\begin{matrix} 0 & 0 & {\cdots } & 0 \\ 0 & 0 & {\cdots } & 0 \\ {\vdots } & {\vdots } & \ddots & {\vdots } \\ \Pi _{u} & \Pi _{u-1} & {\cdots } & \Pi _{v+1} \\ 0 & 0 & {\cdots } & 0 \\ {\vdots } & {\vdots } & \ddots & {\vdots } \\ 0 & 0 & {\cdots } & 0 \\ \end{matrix}\right], ~ ~ G = \left[\begin{matrix} V_{0} & I_ k \\ V_{1} & \Psi _{1} \\ {\vdots } & {\vdots } \\ V_{v-1} & \Psi _{v-1} \\ I_ r & 0_{r\times k} \\ \Psi ^ x_{1} & 0_{r\times k} \\ {\vdots } & {\vdots } \\ \Psi ^ x_{v-1} & 0_{r\times k} \\ \end{matrix}\right] \]](images/etsug_varmax0329.png) |
and
|
|
Note that the matrix ![]() and the input vector
and the input vector ![]() are defined only when
are defined only when ![]() .
.