The SEVERITY Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Predefined DistributionsCensoring and TruncationParameter Estimation MethodParameter InitializationEstimating Regression EffectsEmpirical Distribution Function Estimation MethodsStatistics of FitDefining a Distribution Model with the FCMP ProcedurePredefined Utility FunctionsCustom Objective FunctionsMultithreaded ComputationInput Data SetsOutput Data SetsDisplayed OutputODS Graphics
Predefined DistributionsCensoring and TruncationParameter Estimation MethodParameter InitializationEstimating Regression EffectsEmpirical Distribution Function Estimation MethodsStatistics of FitDefining a Distribution Model with the FCMP ProcedurePredefined Utility FunctionsCustom Objective FunctionsMultithreaded ComputationInput Data SetsOutput Data SetsDisplayed OutputODS Graphics -
Examples

- References
Empirical Distribution Function Estimation Methods
The empirical distribution function (EDF) is a nonparametric estimate of the cumulative distribution function (CDF) of the distribution. PROC SEVERITY uses EDF estimates for computing the EDF-based statistics of fit.
If you specify both right-censoring and left-censoring, then the EDF is estimated using Turnbull’s method as described in the section EDF Estimation for Right-Censored and Left-Censored Data. If all the observations are uncensored or there is only one type of censoring, then a choice of methods is available as described in the section EDF Estimation for No Censoring or Single Type of Censoring.
Notation
Let there be a set of ![]() observations, each containing a quintuplet of values
observations, each containing a quintuplet of values ![]() , where
, where ![]() is the value of the response variable,
is the value of the response variable, ![]() is the value of the left-truncation threshold,
is the value of the left-truncation threshold, ![]() is the value of the right-truncation threshold,
is the value of the right-truncation threshold, ![]() is the value of the right-censoring limit, and
is the value of the right-censoring limit, and ![]() is the value of the left-censoring limit.
is the value of the left-censoring limit.
If an observation is not left-truncated, then ![]() , where
, where ![]() is the smallest value in the support of the distribution; so
is the smallest value in the support of the distribution; so ![]() . If an observation is not right-truncated, then
. If an observation is not right-truncated, then ![]() , where
, where ![]() is the largest value in the support of the distribution; so
is the largest value in the support of the distribution; so ![]() . If an observation is not right-censored, then
. If an observation is not right-censored, then ![]() ; so
; so ![]() . If an observation is not left-censored, then
. If an observation is not left-censored, then ![]() ; so
; so ![]() .
.
Let ![]() denote the weight associated with
denote the weight associated with ![]() th observation. If you have specified the WEIGHT statement, then
th observation. If you have specified the WEIGHT statement, then ![]() is the normalized value of the weight variable; otherwise, it is set to 1. The weights are normalized such that they sum
up to
is the normalized value of the weight variable; otherwise, it is set to 1. The weights are normalized such that they sum
up to ![]() .
.
An indicator function ![]() takes a value of 1 or 0 if the expression
takes a value of 1 or 0 if the expression ![]() is true or false, respectively.
is true or false, respectively.
EDF Estimation for No Censoring or Single Type of Censoring
The method descriptions assume that all observations are either uncensored or right-censored; that is, each observation is
of the form ![]() .
.
If all observations are either uncensored or left-censored, then each observation is of the form ![]() . It is converted to an observation
. It is converted to an observation ![]() ; that is, the signs of all the response variable values are reversed, the new left-truncation threshold is equal to the negative
of the original right-truncation threshold, the new right-truncation threshold is equal to the negative of the original left-truncation
threshold, and the negative of the original left-censoring limit becomes the new right-censoring limit. With this transformation,
each observation is either uncensored or right-censored. The methods described for handling uncensored or right-censored data
are now applicable. After the EDF estimates are computed, the observations are transformed back to the original form and EDF
estimates are adjusted such
; that is, the signs of all the response variable values are reversed, the new left-truncation threshold is equal to the negative
of the original right-truncation threshold, the new right-truncation threshold is equal to the negative of the original left-truncation
threshold, and the negative of the original left-censoring limit becomes the new right-censoring limit. With this transformation,
each observation is either uncensored or right-censored. The methods described for handling uncensored or right-censored data
are now applicable. After the EDF estimates are computed, the observations are transformed back to the original form and EDF
estimates are adjusted such ![]() , where
, where ![]() denotes the EDF estimate of the value slightly less than the transformed value
denotes the EDF estimate of the value slightly less than the transformed value ![]() .
.
A set of uncensored or right-censored observations can be converted to a set of observations of the form ![]() , where
, where ![]() is the indicator of right-censoring.
is the indicator of right-censoring. ![]() indicates a right-censored observation, in which case
indicates a right-censored observation, in which case ![]() is assumed to record the right-censoring limit
is assumed to record the right-censoring limit ![]() .
. ![]() indicates an uncensored observation, and
indicates an uncensored observation, and ![]() records the exact observed value. In other words,
records the exact observed value. In other words, ![]() and
and ![]() .
.
Given this notation, the EDF is estimated as
![\[ F_ n(y) = \left\{ \begin{array}{ll} 0 & \text { if } y < y^{(1)} \\ \hat{F}_ n(y^{(k)}) & \text { if } y^{(k)} \leq y < y^{(k+1)}, k = 1, \dotsc , N-1 \\ \hat{F}_ n(y^{(N)}) & \text { if } y^{(N)} \leq y \end{array} \right. \]](images/etsug_severity0439.png) |
where ![]() denotes the
denotes the ![]() th order statistic of the set
th order statistic of the set ![]() and
and ![]() is the estimate computed at that value. The definition of
is the estimate computed at that value. The definition of ![]() depends on the estimation method. You can specify a particular method or let PROC SEVERITY choose an appropriate method by
using the EMPIRICALCDF= option in the PROC SEVERITY statement. Each method computes
depends on the estimation method. You can specify a particular method or let PROC SEVERITY choose an appropriate method by
using the EMPIRICALCDF= option in the PROC SEVERITY statement. Each method computes ![]() as follows:
as follows:
- STANDARD
-
This method is the standard way of computing EDF. The EDF estimate at observation
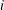 is computed as follows:
is computed as follows:
![\[ \hat{F}_ n(y_ i) = \frac{1}{N} {\displaystyle \sum _{j=1}^{N} w_ j \cdot I[y_ j \leq y_ i]} \]](images/etsug_severity0444.png)
This method ignores any censoring and truncation information, even if it is specified. When no censoring or truncation information is specified, this is the default method chosen.
The standard error of
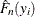 is computed by using the normal approximation method:
is computed by using the normal approximation method:
![\[ \hat{\sigma }_ n(y_ i) = \sqrt {\hat{F}_ n(y_ i) (1-\hat{F}_ n(y_ i))/N} \]](images/etsug_severity0446.png)
- KAPLANMEIER
-
The Kaplan-Meier (KM) estimator, also known as the product-limit estimator, was first introduced by Kaplan and Meier (1958) for censored data. Lynden-Bell (1971) derived a similar estimator for left-truncated data. PROC SEVERITY uses the definition that combines both censoring and truncation information (Klein and Moeschberger 1997, Lai and Ying 1991).
The EDF estimate at observation
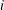 is computed as
is computed as
![\[ \hat{F}_ n(y_ i) = 1 - {\displaystyle \prod _{\tau \leq y_ i} \left(1 - \frac{n(\tau )}{R_ n(\tau )} \right)} \]](images/etsug_severity0447.png)
where
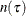 and
and 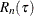 are defined as follows:
are defined as follows:
-
![$n(\tau ) = \sum _{k=1}^{N} w_ k \cdot I[y_ k = \tau \text { and } \tau \leq t^ r_ k \text { and } \delta _ k = 1]$](images/etsug_severity0450.png) , which is the number of uncensored observations (
, which is the number of uncensored observations (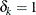 ) for which the response variable value is equal to
) for which the response variable value is equal to  and
and  is observable according to the right-truncation threshold of that observation (
is observable according to the right-truncation threshold of that observation (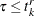 ).
).
-
![$R_ n(\tau ) = \sum _{k=1}^{N} w_ k \cdot I[y_ k \geq \tau > t^ l_ k]$](images/etsug_severity0453.png) , which is the size (cardinality) of the risk set at
, which is the size (cardinality) of the risk set at  . The term risk set has its origins in survival analysis; it contains the events that are at risk of failure at a given time,
. The term risk set has its origins in survival analysis; it contains the events that are at risk of failure at a given time,  . In other words, it contains the events that have survived up to time
. In other words, it contains the events that have survived up to time  and might fail at or after
and might fail at or after  . For PROC SEVERITY, time is equivalent to the magnitude of the event and failure is equivalent to an uncensored and observable event, where observable means it satisfies the truncation thresholds.
. For PROC SEVERITY, time is equivalent to the magnitude of the event and failure is equivalent to an uncensored and observable event, where observable means it satisfies the truncation thresholds.
If you do not explicitly specify a method of computing EDF, then this is the default method used if you specify either right-censoring or left-censoring, but not both. This is also the default method when you specify truncation without any censoring.
The standard error of
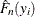 is computed by using Greenwood’s formula (Greenwood, 1926):
is computed by using Greenwood’s formula (Greenwood, 1926):
![\[ \hat{\sigma }_ n(y_ i) = \sqrt {(1-\hat{F}_ n(y_ i))^2 \cdot \sum _{\tau \leq y_ i} \left( \frac{n(\tau )}{R_ n(\tau ) (R_ n(\tau )-n(\tau ))} \right)} \]](images/etsug_severity0454.png)
-
- MODIFIEDKM
-
The product-limit estimator used by the KAPLANMEIER method does not work well if the risk set size becomes very small. For right-censored data, the size can become small towards the right tail. For left-truncated data, the size can become small at the left tail and can remain so for the entire range of data. This was demonstrated by Lai and Ying (1991). They proposed a modification to the estimator that ignores the effects due to small risk set sizes.
The EDF estimate at observation
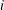 is computed as
is computed as
![\[ \hat{F}_ n(y_ i) = 1 - {\displaystyle \prod _{\tau \leq y_ i} \left(1 - \frac{n(\tau )}{R_ n(\tau )} \cdot I[R_ n(\tau ) \geq c N^\alpha ] \right)} \]](images/etsug_severity0455.png)
where the definitions of
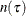 and
and 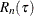 are identical to those used for the KAPLANMEIER method described previously.
are identical to those used for the KAPLANMEIER method described previously.
You can specify the values of
 and
and  by using the C= and ALPHA= options. If you do not specify a value for
by using the C= and ALPHA= options. If you do not specify a value for  , the default value used is
, the default value used is 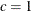 . If you do not specify a value for
. If you do not specify a value for  , the default value used is
, the default value used is 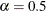 .
.
As an alternative, you can also specify an absolute lower bound, say
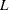 , on the risk set size by using the RSLB= option, in which case
, on the risk set size by using the RSLB= option, in which case ![$I[R_ n(\tau ) \geq c N^\alpha ]$](images/etsug_severity0456.png) is replaced by
is replaced by ![$I[R_ n(\tau ) \geq L]$](images/etsug_severity0457.png) in the definition.
in the definition.
The standard error of
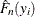 is computed by using Greenwood’s formula (Greenwood, 1926):
is computed by using Greenwood’s formula (Greenwood, 1926):
![\[ \hat{\sigma }_ n(y_ i) = \sqrt {(1-\hat{F}_ n(y_ i))^2 \cdot \sum _{\tau \leq y_ i} \left(\frac{n(\tau )}{R_ n(\tau ) (R_ n(\tau )-n(\tau ))} \cdot I[R_ n(\tau ) \geq c N^\alpha ] \right)} \]](images/etsug_severity0458.png)
If the response variable is subject to both left-censoring and right-censoring effects, then the SEVERITY procedure uses a method proposed by Turnbull (1976) to compute the nonparametric estimates of the cumulative distribution function. The original Turnbull’s method is modified using the suggestions made by Frydman (1994) when truncation effects are present.
Let the input data consist of ![]() observations in the form of quintuplets of values
observations in the form of quintuplets of values ![]() with notation described in the section Notation. For each observation, let
with notation described in the section Notation. For each observation, let ![]() be the censoring interval; that is, the response variable value is known to lie in the interval
be the censoring interval; that is, the response variable value is known to lie in the interval ![]() , but the exact value is not known. If an observation is uncensored, then
, but the exact value is not known. If an observation is uncensored, then ![]() for any arbitrarily small value of
for any arbitrarily small value of ![]() . If an observation is censored, then the value
. If an observation is censored, then the value ![]() is ignored. Similarly, for each observation, let
is ignored. Similarly, for each observation, let ![]() be the truncation interval; that is, the observation is drawn from a truncated (conditional) distribution
be the truncation interval; that is, the observation is drawn from a truncated (conditional) distribution ![]() .
.
Two sets, ![]() and
and ![]() , are formed using
, are formed using ![]() and
and ![]() as follows:
as follows:
|
|
|
|
|
|
The sets ![]() and
and ![]() represent the left endpoints and right endpoints, respectively. A set of disjoint intervals
represent the left endpoints and right endpoints, respectively. A set of disjoint intervals ![]() ,
, ![]() is formed such that
is formed such that ![]() and
and ![]() and
and ![]() and
and ![]() . The value of
. The value of ![]() is dependent on the nature of censoring and truncation intervals in the input data. Turnbull (1976) showed that the maximum
likelihood estimate (MLE) of the EDF can increase only inside intervals
is dependent on the nature of censoring and truncation intervals in the input data. Turnbull (1976) showed that the maximum
likelihood estimate (MLE) of the EDF can increase only inside intervals ![]() . In other words, the MLE estimate is constant in the interval
. In other words, the MLE estimate is constant in the interval ![]() . The likelihood is independent of the behavior of
. The likelihood is independent of the behavior of ![]() inside any of the intervals
inside any of the intervals ![]() . Let
. Let ![]() denote the increase in
denote the increase in ![]() inside an interval
inside an interval ![]() . Then, the EDF estimate is as follows:
. Then, the EDF estimate is as follows:
![\[ F_ n(y) = \left\{ \begin{array}{ll} 0 & \text { if } y < q_1 \\ \sum _{k=1}^{j} s_ k & \text { if } p_ j < y < q_{j+1}, 1 \leq j \leq M-1 \\ 1 & \text { if } y > p_ M \end{array} \right. \]](images/etsug_severity0483.png) |
PROC SEVERITY reports the estimates ![]() at points
at points ![]() and
and ![]() and reports
and reports ![]() at point
at point ![]() , where
, where ![]() denotes the limiting estimate at a point that is infinitesimally larger than
denotes the limiting estimate at a point that is infinitesimally larger than ![]() when approaching
when approaching ![]() from values larger than
from values larger than ![]() and where
and where ![]() denotes the limiting estimate at a point that is infinitesimally smaller than
denotes the limiting estimate at a point that is infinitesimally smaller than ![]() when approaching
when approaching ![]() from values smaller than
from values smaller than ![]() .
.
PROC SEVERITY uses the expectation-maximization (EM) algorithm proposed by Turnbull (1976), who referred to the algorithm as the self-consistency algorithm. By default, the algorithm runs until one of the following criteria is met:
-
Relative-error criterion: The maximum relative error between the two consecutive estimates of
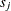 falls below a threshold
falls below a threshold  . If
. If 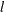 indicates an index of the current iteration, then this can be formally stated as
indicates an index of the current iteration, then this can be formally stated as
![\[ \arg \max _{1 \leq j \leq M} \left\lbrace \frac{|s_ j^{l} - s_ j^{l-1}|}{s_ j^{l-1}} \right\rbrace \leq \epsilon \]](images/etsug_severity0491.png)
You can control the value of
 by specifying the EPS= suboption of the EDF=TURNBULL option in the PROC SEVERITY statement. The default value is 1.0E–8.
by specifying the EPS= suboption of the EDF=TURNBULL option in the PROC SEVERITY statement. The default value is 1.0E–8.
-
Maximum-iteration criterion: The number of iterations exceeds an upper limit specified by the MAXITER= suboption of the EDF=TURNBULL option in the PROC SEVERITY statement. The default number of maximum iterations is
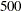 .
.
The self-consistent estimates obtained in this manner might not be maximum likelihood estimates. Gentleman and Geyer (1994)
suggested the use of the Kuhn-Tucker conditions for the maximum likelihood problem to ensure that the estimates are MLE. If
you specify the ENSUREMLE suboption of the EDF=TURNBULL option in the PROC SEVERITY statement, then PROC SEVERITY computes the Kuhn-Tucker conditions
at the end of each iteration to determine whether the estimates {![]() } are MLE. If no truncation effects are specified, then the Kuhn-Tucker conditions derived by Gentleman and Geyer (1994) are
used. If truncation effects are specified, then PROC SEVERITY uses modified Kuhn-Tucker conditions that account for the truncation
effects. An integral part of checking the conditions is to determine whether an estimate
} are MLE. If no truncation effects are specified, then the Kuhn-Tucker conditions derived by Gentleman and Geyer (1994) are
used. If truncation effects are specified, then PROC SEVERITY uses modified Kuhn-Tucker conditions that account for the truncation
effects. An integral part of checking the conditions is to determine whether an estimate ![]() is zero or whether an estimate of the Lagrange multiplier or the reduced gradient associated with the estimate
is zero or whether an estimate of the Lagrange multiplier or the reduced gradient associated with the estimate ![]() is zero. PROC SEVERITY declares these values to be zero if they are less than or equal to a threshold
is zero. PROC SEVERITY declares these values to be zero if they are less than or equal to a threshold ![]() . You can control the value of
. You can control the value of ![]() by specifying the ZEROPROB= suboption of the EDF=TURNBULL option in the PROC SEVERITY statement. The default value is 1.0E–8. The algorithm continues
until the Kuhn-Tucker conditions are satisfied or the number of iterations exceeds the upper limit. The relative-error criterion
stated previously is not used when the ENSUREMLE option is specified.
by specifying the ZEROPROB= suboption of the EDF=TURNBULL option in the PROC SEVERITY statement. The default value is 1.0E–8. The algorithm continues
until the Kuhn-Tucker conditions are satisfied or the number of iterations exceeds the upper limit. The relative-error criterion
stated previously is not used when the ENSUREMLE option is specified.
The standard errors for Turnbull’s EDF estimates are computed by using the asymptotic theory of the maximum likelihood estimators
(MLE), even though the final estimates might not be MLE. Turnbull’s estimator essentially attempts to maximize the likelihood
![]() , which depends on the parameters
, which depends on the parameters ![]() (
(![]() ). Let
). Let ![]() denote the set of these parameters. If
denote the set of these parameters. If ![]() denotes the Hessian matrix of the negative of log likelihood, then the variance-covariance matrix of
denotes the Hessian matrix of the negative of log likelihood, then the variance-covariance matrix of ![]() is estimated as
is estimated as ![]() . Given this matrix, the standard error of
. Given this matrix, the standard error of ![]() is computed as
is computed as
![\[ \sigma _ n(y) = \sqrt {\sum _{k=1}^{j} \left( \hat{C}_{kk} + 2 \cdot \sum _{l=1}^{k-1} \hat{C}_{kl} \right)} \text {, if } p_ j < y < q_{j+1}, 1 \leq j \leq M-1 \]](images/etsug_severity0500.png) |
The standard error is undefined outside of these intervals.
EDF Estimates and Truncation
If truncation is specified, then the estimate ![]() computed by any method other than the STANDARD method is a conditional estimate. In other words,
computed by any method other than the STANDARD method is a conditional estimate. In other words, ![]() , where
, where ![]() and
and ![]() denote the (unknown) distribution functions of the left-truncation threshold variable
denote the (unknown) distribution functions of the left-truncation threshold variable ![]() and the right-truncation threshold variable
and the right-truncation threshold variable ![]() , respectively,
, respectively, ![]() denotes the smallest left-truncation threshold with a nonzero cumulative probability, and
denotes the smallest left-truncation threshold with a nonzero cumulative probability, and ![]() denotes the largest right-truncation threshold with a nonzero cumulative probability. Formally,
denotes the largest right-truncation threshold with a nonzero cumulative probability. Formally, ![]() and
and ![]() . For computational purposes, PROC SEVERITY estimates
. For computational purposes, PROC SEVERITY estimates ![]() and
and ![]() by
by ![]() and
and ![]() , respectively, defined as
, respectively, defined as
|
|
|
|
|
|
These estimates are used to compute conditional estimates of the CDF as described in the section Truncation and Conditional CDF Estimates.
If left-truncation is specified with the probability of observability ![]() , then PROC SEVERITY uses the additional information provided by
, then PROC SEVERITY uses the additional information provided by ![]() to compute an estimate of the EDF that is not conditional on the left-truncation information. In particular, for each left-truncated
observation
to compute an estimate of the EDF that is not conditional on the left-truncation information. In particular, for each left-truncated
observation ![]() with response variable value
with response variable value ![]() and truncation threshold
and truncation threshold ![]() , an observation
, an observation ![]() is added with weight
is added with weight ![]() and
and ![]() . Each added observation is assumed to be uncensored and untruncated. Then, the specified EDF method is used by assuming no
left-truncation. The EDF estimate that is obtained using this method is not conditional on the left-truncation information.
For the KAPLANMEIER and MODIFIEDKM methods with uncensored or right-censored data, definitions of
. Each added observation is assumed to be uncensored and untruncated. Then, the specified EDF method is used by assuming no
left-truncation. The EDF estimate that is obtained using this method is not conditional on the left-truncation information.
For the KAPLANMEIER and MODIFIEDKM methods with uncensored or right-censored data, definitions of ![]() and
and ![]() are modified to account for the added observations. If
are modified to account for the added observations. If ![]() denotes the total number of observations including the added observations, then
denotes the total number of observations including the added observations, then ![]() is defined as
is defined as ![]() , and
, and ![]() is defined as
is defined as ![]() . In the definition of
. In the definition of ![]() , the left-truncation information is not used, because it was used along with
, the left-truncation information is not used, because it was used along with ![]() to add the observations.
to add the observations.
If the original data are a combination of left- and right-censored data, then Turnbull’s method is applied to the appended set that contains no left-truncated observations.
Supplying EDF Estimates to Functions and Subroutines
The parameter initialization subroutines in distribution models and some predefined utility functions require EDF estimates. See the sections Defining a Distribution Model with the FCMP Procedure and Predefined Utility Functions for more information.
PROC SEVERITY supplies the EDF estimates to these subroutines and functions by using two arrays, x and F, the dimension of each array, and a type of the EDF estimates. The type identifies how the EDF estimates are computed and
stored. They are as follows:
- Type 1
-
specifies that EDF estimates are computed using the STANDARD method; that is, the data used for estimation are neither censored nor truncated.
- Type 2
-
specifies that EDF estimates are computed using either the KAPLANMEIER or the MODIFIEDKM method; that is, the data used for estimation are subject to truncation and one type of censoring (left or right, but not both).
- Type 3
-
specifies that EDF estimates are computed using the TURNBULL method; that is, the data used for estimation are subject to both left- and right-censoring. The data might or might not be truncated.
For Types 1 and 2, the EDF estimates are stored in arrays x and F of dimension N such that the following holds:
![\[ F_ n(y) = \left\{ \begin{array}{ll} 0 & \text { if } y < x[1] \\ F[k] & \text { if } x[k] \leq y < x[k+1], k = 1, \dotsc , N-1 \\ F[N] & \text { if } x[N] \leq y \end{array} \right. \]](images/etsug_severity0520.png) |
where ![]() denotes
denotes ![]() th element of the array ([1] denotes the first element of the array).
th element of the array ([1] denotes the first element of the array).
For Type 3, the EDF estimates are stored in arrays x and F of dimension N such that the following holds:
![\[ F_ n(y) = \left\{ \begin{array}{ll} 0 & \text { if } y < x[1] \\ \text {undefined} & \text { if } x[2k-1] \leq y < x[2k], k = 1, \dotsc , (N-1)/2 \\ F[2k] = F[2k+1] & \text { if } x[2k] \leq y < x[2k+1], k = 1, \dotsc , (N-1)/2 \\ F[N] & \text { if } x[N] \leq y \end{array} \right. \]](images/etsug_severity0522.png) |
Although the behavior of EDF is theoretically undefined for the interval ![]() , for computational purposes, all predefined functions and subroutines assume that the EDF increases linearly from
, for computational purposes, all predefined functions and subroutines assume that the EDF increases linearly from ![]() to
to ![]() in that interval if
in that interval if ![]() . If
. If ![]() , which can happen when the EDF is estimated from a combination of uncensored and interval-censored data, the predefined functions
and subroutines assume that
, which can happen when the EDF is estimated from a combination of uncensored and interval-censored data, the predefined functions
and subroutines assume that ![]() .
.