The SEVERITY Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Predefined DistributionsCensoring and TruncationParameter Estimation MethodParameter InitializationEstimating Regression EffectsEmpirical Distribution Function Estimation MethodsStatistics of FitDefining a Distribution Model with the FCMP ProcedurePredefined Utility FunctionsCustom Objective FunctionsMultithreaded ComputationInput Data SetsOutput Data SetsDisplayed OutputODS Graphics
Predefined DistributionsCensoring and TruncationParameter Estimation MethodParameter InitializationEstimating Regression EffectsEmpirical Distribution Function Estimation MethodsStatistics of FitDefining a Distribution Model with the FCMP ProcedurePredefined Utility FunctionsCustom Objective FunctionsMultithreaded ComputationInput Data SetsOutput Data SetsDisplayed OutputODS Graphics -
Examples

- References
Predefined Distributions
PROC SEVERITY assumes the following model for the response variable ![]()
|
|
where ![]() is a continuous probability distribution with parameters
is a continuous probability distribution with parameters ![]() . The model hypothesizes that the observed response is generated from a stochastic process that is governed by the distribution
. The model hypothesizes that the observed response is generated from a stochastic process that is governed by the distribution
![]() . This model is typically referred to as the error model. Given a representative input sample of response variable values,
PROC SEVERITY estimates the model parameters for any distribution
. This model is typically referred to as the error model. Given a representative input sample of response variable values,
PROC SEVERITY estimates the model parameters for any distribution ![]() and computes the statistics of fit for each model. This enables you to find the distribution that is most likely to generate
the observed sample.
and computes the statistics of fit for each model. This enables you to find the distribution that is most likely to generate
the observed sample.
A set of predefined distributions is provided with the SEVERITY procedure. A summary of the distributions is provided in Table 23.2. For each distribution, the table lists the name of the distribution that should be used in the DIST statement, the parameters of the distribution along with their bounds, and the mathematical expressions for the probability density function (PDF) and cumulative distribution function (CDF) of the distribution.
All the predefined distributions, except LOGN and TWEEDIE, are parameterized such that their first parameter is the scale
parameter. For LOGN, the first parameter ![]() is a log-transformed scale parameter. TWEEDIE does not have a scale parameter. The presence of scale parameter or a log-transformed
scale parameter enables you to use all of the predefined distributions, except TWEEDIE, as a candidate for estimating regression
effects.
is a log-transformed scale parameter. TWEEDIE does not have a scale parameter. The presence of scale parameter or a log-transformed
scale parameter enables you to use all of the predefined distributions, except TWEEDIE, as a candidate for estimating regression
effects.
A distribution model is associated with each predefined distribution. You can also define your own distribution model, which is a set of functions and subroutines that you define by using the FCMP procedure. See the section Defining a Distribution Model with the FCMP Procedure for more information.
Table 23.2: Predefined SEVERITY Distributions
|
Name |
Distribution |
Parameters |
PDF ( |
|
|---|---|---|---|---|
|
BURR |
Burr |
|
|
|
|
|
|
|
||
|
EXP |
Exponential |
|
|
|
|
|
|
|||
|
GAMMA |
Gamma |
|
|
|
|
|
|
|||
|
GPD |
Generalized |
|
|
|
|
Pareto |
|
|
||
|
IGAUSS |
Inverse Gaussian |
|
|
|
|
(Wald) |
|
|
||
|
|
||||
|
LOGN |
Lognormal |
|
|
|
|
|
|
|
||
|
PARETO |
Pareto |
|
|
|
|
|
|
|||
|
TWEEDIE |
Tweedie |
|
|
|
|
|
|
|
||
|
STWEEDIE |
Scaled Tweedie |
|
|
|
|
|
|
|
||
|
WEIBULL |
Weibull |
|
|
|
|
|
|
|||
|
Notes: |
||||
|
1. |
||||
|
2. |
||||
|
3. Parameters are listed in the order in which they are defined in the distribution model. |
||||
|
4. |
||||
|
5. |
||||
|
6. See the section Tweedie Distributions for more information. |
||||
Tweedie Distributions
Tweedie distributions are a special case of the exponential dispersion family (Jørgensen, 1987) with a property that the
variance of the distribution is equal to ![]() , where
, where ![]() is the mean of the distribution,
is the mean of the distribution, ![]() is a dispersion parameter, and
is a dispersion parameter, and ![]() is an index parameter as discovered by Tweedie (1984). The distribution is defined for all values of
is an index parameter as discovered by Tweedie (1984). The distribution is defined for all values of ![]() except for values of
except for values of ![]() in the open interval
in the open interval ![]() . Many important known distributions are a special case of Tweedie distributions including normal (
. Many important known distributions are a special case of Tweedie distributions including normal (![]() =0), Poisson (
=0), Poisson (![]() =1), gamma (
=1), gamma (![]() =2), and the inverse Gaussian (
=2), and the inverse Gaussian (![]() =3). Apart from these special cases, the probability density function (PDF) of the Tweedie distribution does not have an analytic
expression. For
=3). Apart from these special cases, the probability density function (PDF) of the Tweedie distribution does not have an analytic
expression. For ![]() , it has the form (Dunn and Smyth 2005),
, it has the form (Dunn and Smyth 2005),
|
|
where ![]() for
for ![]() and
and ![]() for
for ![]() . The function
. The function ![]() does not have an analytical expression. It is typically evaluated using series expansion methods described in Dunn and Smyth
(2005).
does not have an analytical expression. It is typically evaluated using series expansion methods described in Dunn and Smyth
(2005).
For ![]() , the Tweedie distribution is a compound Poisson-gamma mixture distribution, which is the distribution of
, the Tweedie distribution is a compound Poisson-gamma mixture distribution, which is the distribution of ![]() defined as
defined as
|
|
where ![]() and
and ![]() are iid gamma random variables with shape parameter
are iid gamma random variables with shape parameter ![]() and scale parameter
and scale parameter ![]() . At
. At ![]() , the density is a probability mass that is governed by the Poisson distribution, and for values of
, the density is a probability mass that is governed by the Poisson distribution, and for values of ![]() , it is a mixture of gamma variates with Poisson mixing probability. The parameters
, it is a mixture of gamma variates with Poisson mixing probability. The parameters ![]() ,
, ![]() and
and ![]() are related to the natural parameters
are related to the natural parameters ![]() ,
, ![]() , and
, and ![]() of the Tweedie distribution as
of the Tweedie distribution as
|
|
|
|
|
|
|
|
|
The mean of a Tweedie distribution is positive for ![]() .
.
Two predefined versions of the Tweedie distribution are provided with the SEVERITY procedure. The first version, named TWEEDIE
and defined for ![]() , has the natural parameterization with parameters
, has the natural parameterization with parameters ![]() ,
, ![]() , and
, and ![]() . The second version, named STWEEDIE and defined for
. The second version, named STWEEDIE and defined for ![]() , is the version with a scale parameter. It corresponds to the compound Poisson-gamma distribution with gamma scale parameter
, is the version with a scale parameter. It corresponds to the compound Poisson-gamma distribution with gamma scale parameter
![]() , Poisson mean parameter
, Poisson mean parameter ![]() , and the index parameter
, and the index parameter ![]() . The index parameter decides the shape parameter
. The index parameter decides the shape parameter ![]() of the gamma distribution as
of the gamma distribution as
|
|
The parameters ![]() and
and ![]() of the STWEEDIE distribution are related to the parameters
of the STWEEDIE distribution are related to the parameters ![]() and
and ![]() of the TWEEDIE distribution as
of the TWEEDIE distribution as
|
|
|
|
|
|
You can fit either version when there are no regression variables. Each version has its own merits. If you fit the TWEEDIE
version, you have the direct estimate of the overall mean of the distribution. If you are interested in the most practical
range of the index parameter ![]() , then you can fit the STWEEDIE version, which provides you direct estimates of the Poisson and gamma components that comprise
the distribution (an estimate of the gamma shape parameter
, then you can fit the STWEEDIE version, which provides you direct estimates of the Poisson and gamma components that comprise
the distribution (an estimate of the gamma shape parameter ![]() is easily obtained from the estimate of
is easily obtained from the estimate of ![]() ).
).
If you want to estimate the effect of exogenous (regression) variables on the distribution, then you must use the STWEEDIE
version, because PROC SEVERITY requires a distribution to have a scale parameter in order to estimate regression effects.
See the section Estimating Regression Effects for more information. The gamma scale parameter ![]() is the scale parameter of the STWEEDIE distribution. If you are interested in determining the effect of regression variables
on the mean of the distribution, you can do so by first fitting the STWEEDIE distribution to determine the effect of the regression
variables on the scale parameter
is the scale parameter of the STWEEDIE distribution. If you are interested in determining the effect of regression variables
on the mean of the distribution, you can do so by first fitting the STWEEDIE distribution to determine the effect of the regression
variables on the scale parameter ![]() . Then, you can easily estimate how the mean of the distribution
. Then, you can easily estimate how the mean of the distribution ![]() is affected by the regression variables using the relationship
is affected by the regression variables using the relationship ![]() , where
, where ![]() . The estimates of the regression parameters remain the same, whereas the estimate of the intercept parameter is adjusted
by the estimates of the
. The estimates of the regression parameters remain the same, whereas the estimate of the intercept parameter is adjusted
by the estimates of the ![]() and
and ![]() parameters.
parameters.
Parameter Initialization for Predefined Distributions
The parameters are initialized by using the method of moments for all the distributions, except for the gamma and the Weibull distributions. For the gamma distribution, approximate maximum likelihood estimates are used. For the Weibull distribution, the method of percentile matching is used.
Given ![]() observations of the severity value
observations of the severity value ![]() (
(![]() ), the estimate of
), the estimate of ![]() th raw moment is denoted by
th raw moment is denoted by ![]() and computed as
and computed as
|
|
The 100![]() th percentile is denoted by
th percentile is denoted by ![]() (
(![]() ). By definition,
). By definition, ![]() satisfies
satisfies
|
|
where ![]() . PROC SEVERITY uses the following practical method of computing
. PROC SEVERITY uses the following practical method of computing ![]() . Let
. Let ![]() denote the empirical distribution function (EDF) estimate at a severity value
denote the empirical distribution function (EDF) estimate at a severity value ![]() . Let
. Let ![]() and
and ![]() denote two consecutive values in the ascending sequence of
denote two consecutive values in the ascending sequence of ![]() values such that
values such that ![]() and
and ![]() . Then, the estimate
. Then, the estimate ![]() is computed as
is computed as
|
|
Let ![]() denote the smallest double-precision floating-point number such that
denote the smallest double-precision floating-point number such that ![]() . This machine precision constant can be obtained by using the CONSTANT function in Base SAS software.
. This machine precision constant can be obtained by using the CONSTANT function in Base SAS software.
The details of how parameters are initialized for each predefined distribution are as follows:
- BURR
-
The parameters are initialized by using the method of moments. The
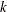 th raw moment of the Burr distribution is:
th raw moment of the Burr distribution is:
![\[ E[X^ k] = \frac{\theta ^ k \Gamma (1 + k/\gamma ) \Gamma (\alpha - k/\gamma )}{\Gamma (\alpha )}, \quad -\gamma < k < \alpha \gamma \]](images/etsug_severity0139.png)
Three moment equations
![$E[X^ k] = m_ k$](images/etsug_severity0140.png) (
( ) need to be solved for initializing the three parameters of the distribution. In order to get an approximate closed form
solution, the second shape parameter
) need to be solved for initializing the three parameters of the distribution. In order to get an approximate closed form
solution, the second shape parameter  is initialized to a value of
is initialized to a value of  . If
. If  , then simplifying and solving the moment equations yields the following feasible set of initial values:
, then simplifying and solving the moment equations yields the following feasible set of initial values:
![\[ \hat{\theta } = \sqrt {\frac{m_2 m_3}{2 m_3 - 3 m_1 m_2}}, \quad \hat{\alpha } = 1 + \frac{m_3}{2 m_3 - 3 m_1 m_2}, \quad \hat{\gamma } = 2 \]](images/etsug_severity0145.png)
If
 , then the parameters are initialized as follows:
, then the parameters are initialized as follows:
![\[ \hat{\theta } = \sqrt {m_2}, \quad \hat{\alpha } = 2, \quad \hat{\gamma } = 2 \]](images/etsug_severity0147.png)
- EXP
-
The parameters are initialized by using the method of moments. The
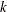 th raw moment of the exponential distribution is:
th raw moment of the exponential distribution is:
![\[ E[X^ k] = \theta ^ k \Gamma (k+1), \quad k > -1 \]](images/etsug_severity0148.png)
Solving
![$E[X] = m_1$](images/etsug_severity0149.png) yields the initial value of
yields the initial value of  .
.
- GAMMA
-
The parameter
 is initialized by using its approximate maximum likelihood (ML) estimate. For a set of
is initialized by using its approximate maximum likelihood (ML) estimate. For a set of  iid observations
iid observations 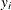 (
( ), drawn from a gamma distribution, the log likelihood,
), drawn from a gamma distribution, the log likelihood, 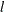 , is defined as follows:
, is defined as follows:




Using a shorter notation of
 to denote
to denote  and solving the equation
and solving the equation  yields the following ML estimate of
yields the following ML estimate of 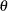 :
:
![\[ \hat{\theta } = \frac{\sum y_ i}{n \alpha } = \frac{m_1}{\alpha } \]](images/etsug_severity0160.png)
Substituting this estimate in the expression of
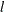 and simplifying gives
and simplifying gives
![\[ l = (\alpha - 1) \sum \log (y_ i) - n \alpha - n \alpha \log (m_1) + n \alpha \log (\alpha ) - n \log (\Gamma (\alpha )) \]](images/etsug_severity0161.png)
Let
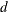 be defined as follows:
be defined as follows:
![\[ d = \log (m_1) - \frac{1}{n} \sum \log (y_ i) \]](images/etsug_severity0163.png)
Solving the equation
 yields the following expression in terms of the digamma function,
yields the following expression in terms of the digamma function,  :
:
![\[ \log (\alpha ) - \psi (\alpha ) = d \]](images/etsug_severity0166.png)
The digamma function can be approximated as follows:
![\[ \hat{\psi }(\alpha ) \approx \log (\alpha ) - \frac{1}{\alpha } \left(0.5 + \frac{1}{12 \alpha + 2}\right) \]](images/etsug_severity0167.png)
This approximation is within 1.4% of the true value for all the values of
 except when
except when  is arbitrarily close to the positive root of the digamma function (which is approximately 1.461632). Even for the values
of
is arbitrarily close to the positive root of the digamma function (which is approximately 1.461632). Even for the values
of  that are close to the positive root, the absolute error between true and approximate values is still acceptable (
that are close to the positive root, the absolute error between true and approximate values is still acceptable ( for
for  ). Solving the equation that arises from this approximation yields the following estimate of
). Solving the equation that arises from this approximation yields the following estimate of  :
:
![\[ \hat{\alpha } = \frac{3 - d + \sqrt {(d-3)^2 + 24 d}}{12 d} \]](images/etsug_severity0170.png)
If this approximate ML estimate is infeasible, then the method of moments is used. The
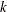 th raw moment of the gamma distribution is:
th raw moment of the gamma distribution is:
![\[ E[X^ k] = \theta ^ k \frac{\Gamma (\alpha + k)}{\Gamma (\alpha )}, \quad k > -\alpha \]](images/etsug_severity0171.png)
Solving
![$E[X] = m_1$](images/etsug_severity0149.png) and
and ![$E[X^2] = m_2$](images/etsug_severity0172.png) yields the following initial value for
yields the following initial value for  :
:
![\[ \hat{\alpha } = \frac{m_1^2}{m_2 - m_1^2} \]](images/etsug_severity0173.png)
If
 (almost zero sample variance), then
(almost zero sample variance), then  is initialized as follows:
is initialized as follows:
![\[ \hat{\alpha } = 1 \]](images/etsug_severity0175.png)
After computing the estimate of
 , the estimate of
, the estimate of 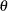 is computed as follows:
is computed as follows:
![\[ \hat{\theta } = \frac{m_1}{\hat{\alpha }} \]](images/etsug_severity0176.png)
Both the maximum likelihood method and the method of moments arrive at the same relationship between
 and
and 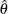 .
.
- GPD
-
The parameters are initialized by using the method of moments. Notice that for
 , the CDF of the generalized Pareto distribution (GPD) is:
, the CDF of the generalized Pareto distribution (GPD) is:




This is equivalent to a Pareto distribution with scale parameter
 and shape parameter
and shape parameter  . Using this relationship, the parameter initialization method used for the PARETO distribution is used to get the following
initial values for the parameters of the GPD distribution:
. Using this relationship, the parameter initialization method used for the PARETO distribution is used to get the following
initial values for the parameters of the GPD distribution:
![\[ \hat{\theta } = \frac{m_1 m_2}{2 (m_2 - m_1^2)}, \quad \hat{\xi } = \frac{m_2 - 2 m_1^2}{2 (m_2 - m_1^2)} \]](images/etsug_severity0185.png)
If
 (almost zero sample variance) or
(almost zero sample variance) or  , then the parameters are initialized as follows:
, then the parameters are initialized as follows:
![\[ \hat{\theta } = \frac{m_1}{2}, \quad \hat{\xi } = \frac{1}{2} \]](images/etsug_severity0187.png)
- IGAUSS
-
The parameters are initialized by using the method of moments. Note that the standard parameterization of the inverse Gaussian distribution (also known as the Wald distribution), in terms of the location parameter
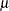 and shape parameter
and shape parameter 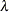 , is as follows (Klugman, Panjer, and Willmot 1998, p. 583):
, is as follows (Klugman, Panjer, and Willmot 1998, p. 583):




For this parameterization, it is known that the mean is
![$E[X] = \mu $](images/etsug_severity0193.png) and the variance is
and the variance is ![$Var[X] = \mu ^3/\lambda $](images/etsug_severity0194.png) , which yields the second raw moment as
, which yields the second raw moment as ![$E[X^2] = \mu ^2 (1 + \mu /\lambda )$](images/etsug_severity0195.png) (computed by using
(computed by using ![$E[X^2] = Var[X] + (E[X])^2$](images/etsug_severity0196.png) ).
).
The predefined IGAUSS distribution in PROC SEVERITY uses the following alternate parameterization to allow the distribution to have a scale parameter,
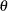 :
:




The parameters
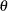 (scale) and
(scale) and  (shape) of this alternate form are related to the parameters
(shape) of this alternate form are related to the parameters 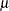 and
and 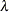 of the preceding form such that
of the preceding form such that  and
and  . Using this relationship, the first and second raw moments of the IGAUSS distribution are:
. Using this relationship, the first and second raw moments of the IGAUSS distribution are:
![$\displaystyle E[X] $](images/etsug_severity0202.png)

![$\displaystyle E[X^2] $](images/etsug_severity0205.png)

Solving
![$E[X] = m_1$](images/etsug_severity0149.png) and
and ![$E[X^2] = m_2$](images/etsug_severity0172.png) yields the following initial values:
yields the following initial values:
![\[ \hat{\theta } = m_1, \quad \hat{\alpha } = \frac{m_1^2}{m_2 - m_1^2} \]](images/etsug_severity0207.png)
If
 (almost zero sample variance), then the parameters are initialized as follows:
(almost zero sample variance), then the parameters are initialized as follows:
![\[ \hat{\theta } = m_1, \quad \hat{\alpha } = 1 \]](images/etsug_severity0208.png)
- LOGN
-
The parameters are initialized by using the method of moments. The
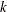 th raw moment of the lognormal distribution is:
th raw moment of the lognormal distribution is:
![\[ E[X^ k] = \exp \left(k \mu + \frac{k^2 \sigma ^2}{2}\right) \]](images/etsug_severity0209.png)
Solving
![$E[X] = m_1$](images/etsug_severity0149.png) and
and ![$E[X^2] = m_2$](images/etsug_severity0172.png) yields the following initial values:
yields the following initial values:
![\[ \hat{\mu } = 2 \log (m1) - \frac{\log (m2)}{2}, \quad \hat{\sigma } = \sqrt {\log (m2) - 2 \log (m1)} \]](images/etsug_severity0210.png)
- PARETO
-
The parameters are initialized by using the method of moments. The
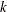 th raw moment of the Pareto distribution is:
th raw moment of the Pareto distribution is:
![\[ E[X^ k] = \frac{\theta ^ k \Gamma (k + 1) \Gamma (\alpha - k)}{\Gamma (\alpha )}, -1 < k < \alpha \]](images/etsug_severity0211.png)
Solving
![$E[X] = m_1$](images/etsug_severity0149.png) and
and ![$E[X^2] = m_2$](images/etsug_severity0172.png) yields the following initial values:
yields the following initial values:
![\[ \hat{\theta } = \frac{m_1 m_2}{m_2 - 2 m_1^2}, \quad \hat{\alpha } = \frac{2(m_2 - m_1^2)}{m_2 - 2 m_1^2} \]](images/etsug_severity0212.png)
If
 (almost zero sample variance) or
(almost zero sample variance) or  , then the parameters are initialized as follows:
, then the parameters are initialized as follows:
![\[ \hat{\theta } = m_1, \quad \hat{\alpha } = 2 \]](images/etsug_severity0213.png)
- TWEEDIE
-
The parameter
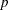 is initialized by assuming that the sample is generated from a gamma distribution with shape parameter
is initialized by assuming that the sample is generated from a gamma distribution with shape parameter  and by computing
and by computing  . The initial value
. The initial value  is obtained from using the method previously described for the GAMMA distribution. The parameter
is obtained from using the method previously described for the GAMMA distribution. The parameter 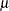 is the mean of the distribution. Hence, it is initialized to the sample mean as
is the mean of the distribution. Hence, it is initialized to the sample mean as
![\[ \hat{\mu } = m_1 \]](images/etsug_severity0215.png)
Variance of a Tweedie distribution is equal to
 . Thus, the sample variance is used to initialize the value of
. Thus, the sample variance is used to initialize the value of 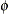 as
as
![\[ \hat{\phi } = \frac{m_2 - m_1^2}{\hat{\mu }^{\hat{p}}} \]](images/etsug_severity0216.png)
- STWEEDIE
-
STWEEDIE is a compound Poisson-gamma mixture distribution with mean
 , where
, where  is the shape parameter of the gamma random variables in the mixture and the parameter
is the shape parameter of the gamma random variables in the mixture and the parameter 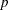 is determined solely by
is determined solely by  . First, the parameter
. First, the parameter 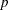 is initialized by assuming that the sample is generated from a gamma distribution with shape parameter
is initialized by assuming that the sample is generated from a gamma distribution with shape parameter  and by computing
and by computing  . The initial value
. The initial value  is obtained from using the method previously described for the GAMMA distribution. As done for initializing the parameters
of the TWEEDIE distribution, the sample mean and variance are used to compute the values
is obtained from using the method previously described for the GAMMA distribution. As done for initializing the parameters
of the TWEEDIE distribution, the sample mean and variance are used to compute the values  and
and  as
as




Based on the relationship between the parameters of TWEEDIE and STWEEDIE distributions described in the section Tweedie Distributions, values of
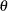 and
and 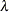 are initialized as
are initialized as




- WEIBULL
-
The parameters are initialized by using the percentile matching method. Let
 and
and  denote the estimates of the
denote the estimates of the  th and
th and  th percentiles, respectively. Using the formula for the CDF of Weibull distribution, they can be written as
th percentiles, respectively. Using the formula for the CDF of Weibull distribution, they can be written as




Simplifying and solving these two equations yields the following initial values:
![\[ \hat{\theta } = \exp \left(\frac{r \log (q1) - \log (q3)}{r - 1}\right), \quad \hat{\tau } = \frac{\log (\log (4))}{\log (q3) - \log (\hat{\theta })} \]](images/etsug_severity0239.png)
where
 . These initial values agree with those suggested in Klugman, Panjer, and Willmot (1998).
. These initial values agree with those suggested in Klugman, Panjer, and Willmot (1998).
A summary of the initial values of all the parameters for all the predefined distributions is given in Table 23.3. The table also provides the names of the parameters to use in the INIT= option in the DIST statement if you want to provide a different initial value.
Table 23.3: Parameter Initialization for Predefined Distributions
|
Distribution |
Parameter |
Name for INIT option |
Default Initial Value |
|---|---|---|---|
|
BURR |
|
theta |
|
|
|
alpha |
|
|
|
|
gamma |
|
|
|
EXP |
|
theta |
|
|
GAMMA |
|
theta |
|
|
|
alpha |
|
|
|
GPD |
|
theta |
|
|
|
xi |
|
|
|
IGAUSS |
|
theta |
|
|
|
alpha |
|
|
|
LOGN |
|
mu |
|
|
|
sigma |
|
|
|
PARETO |
|
theta |
|
|
|
alpha |
|
|
|
TWEEDIE |
|
mu |
|
|
|
phi |
|
|
|
|
p |
|
|
|
where |
|||
|
STWEEDIE |
|
theta |
|
|
|
lambda |
|
|
|
|
p |
|
|
|
where |
|||
|
WEIBULL |
|
theta |
|
|
|
tau |
|
|
|
Notes: |
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||