The SEVERITY Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Predefined DistributionsCensoring and TruncationParameter Estimation MethodParameter InitializationEstimating Regression EffectsEmpirical Distribution Function Estimation MethodsStatistics of FitDefining a Distribution Model with the FCMP ProcedurePredefined Utility FunctionsCustom Objective FunctionsMultithreaded ComputationInput Data SetsOutput Data SetsDisplayed OutputODS Graphics
Predefined DistributionsCensoring and TruncationParameter Estimation MethodParameter InitializationEstimating Regression EffectsEmpirical Distribution Function Estimation MethodsStatistics of FitDefining a Distribution Model with the FCMP ProcedurePredefined Utility FunctionsCustom Objective FunctionsMultithreaded ComputationInput Data SetsOutput Data SetsDisplayed OutputODS Graphics -
Examples

- References
Estimating Regression Effects
The SEVERITY procedure enables you to estimate the effects of regressor (exogenous) variables while fitting a distribution if the distribution has a scale parameter or a log-transformed scale parameter.
Let ![]() (
(![]() ) denote the
) denote the ![]() regressor variables. Let
regressor variables. Let ![]() denote the regression parameter that corresponds to the regressor
denote the regression parameter that corresponds to the regressor ![]() . If regression effects are not specified, then the model for the response variable
. If regression effects are not specified, then the model for the response variable ![]() is of the form
is of the form
|
|
where ![]() is the distribution of
is the distribution of ![]() with parameters
with parameters ![]() . This model is typically referred to as the error model. The regression effects are modeled by extending the error model
to the following form:
. This model is typically referred to as the error model. The regression effects are modeled by extending the error model
to the following form:
|
|
Under this model, the distribution of ![]() is valid and belongs to the same parametric family as
is valid and belongs to the same parametric family as ![]() if and only if
if and only if ![]() has a scale parameter. Let
has a scale parameter. Let ![]() denote the scale parameter and
denote the scale parameter and ![]() denote the set of nonscale distribution parameters of
denote the set of nonscale distribution parameters of ![]() . Then the model can be rewritten as
. Then the model can be rewritten as
|
|
such that ![]() is affected by the regressors as
is affected by the regressors as
|
|
where ![]() is the base value of the scale parameter. Thus, the regression model consists of the following parameters:
is the base value of the scale parameter. Thus, the regression model consists of the following parameters: ![]() ,
, ![]() , and
, and ![]() .
.
Given this form of the model, distributions without a scale parameter cannot be considered when regression effects are to
be modeled. If a distribution does not have a direct scale parameter, then PROC SEVERITY accepts it only if it has a log-transformed
scale parameter — that is, if it has a parameter ![]() .
.
Parameter Initialization for Regression Models
The regression parameters are initialized either by using the values you specify or by the default method.
-
If you provide initial values for the regression parameters, then you must provide valid, nonmissing initial values for
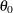 and
and 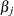 parameters for all
parameters for all 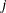 .
.
You can specify the initial value for
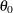 using either the INEST= data set or the INIT= option in the DIST statement. If the distribution has a direct scale parameter
(no transformation), then the initial value for the first parameter of the distribution is used as an initial value for
using either the INEST= data set or the INIT= option in the DIST statement. If the distribution has a direct scale parameter
(no transformation), then the initial value for the first parameter of the distribution is used as an initial value for 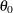 . If the distribution has a log-transformed scale parameter, then the initial value for the first parameter of the distribution
is used as an initial value for
. If the distribution has a log-transformed scale parameter, then the initial value for the first parameter of the distribution
is used as an initial value for  .
.
You can use only the INEST= data set to specify the initial values for
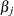 . The INEST= data set must contain nonmissing initial values for all the regressors specified in the SCALEMODEL statement.
The only missing value allowed is the special missing value .R, which indicates that the regressor is linearly dependent on
other regressors. If you specify .R for a regressor for one distribution in a BY group, you must specify it so for all the
distributions in that BY group.
. The INEST= data set must contain nonmissing initial values for all the regressors specified in the SCALEMODEL statement.
The only missing value allowed is the special missing value .R, which indicates that the regressor is linearly dependent on
other regressors. If you specify .R for a regressor for one distribution in a BY group, you must specify it so for all the
distributions in that BY group.
-
If you do not specify valid initial values for
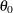 or
or 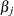 parameters for all
parameters for all 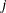 , then PROC SEVERITY initializes those parameters using the following method:
, then PROC SEVERITY initializes those parameters using the following method:
Let a random variable
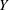 be distributed as
be distributed as  , where
, where 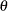 is the scale parameter. By definition of the scale parameter, a random variable
is the scale parameter. By definition of the scale parameter, a random variable  is distributed as
is distributed as  such that
such that  . Given a random error term
. Given a random error term  that is generated from a distribution
that is generated from a distribution  , a value
, a value 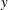 from the distribution of
from the distribution of 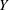 can be generated as
can be generated as
![\[ y = \theta \cdot e \]](images/etsug_severity0357.png)
Taking the logarithm of both sides and using the relationship of
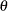 with the regressors yields:
with the regressors yields:
![\[ \log (y) = \log (\theta _0) + \sum _{j=1}^{k} \beta _ j x_ j + \log (e) \]](images/etsug_severity0358.png)
PROC SEVERITY makes use of the preceding relationship to initialize parameters of a regression model with distribution dist as follows:
-
The following linear regression problem is solved to obtain initial estimates of
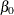 and
and 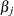 :
:
![\[ \log (y) = \beta _0 + \sum _{j=1}^{k} \beta _ j x_ j \]](images/etsug_severity0360.png)
The estimates of
 in the solution of this regression problem are used to initialize the respective regression parameters of the model. The
estimate of
in the solution of this regression problem are used to initialize the respective regression parameters of the model. The
estimate of 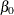 is later used to initialize the value of
is later used to initialize the value of 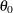 .
.
The results of this regression are also used to detect whether any regressors are linearly dependent on the other regressors. If any such regressors are found, then a warning is written to the SAS log and the corresponding regressor is eliminated from further analysis. The estimates for linearly dependent regressors are denoted by a special missing value of .R in the OUTEST= data set and in any displayed output.
-
Let
 denote the initial value of the scale parameter.
denote the initial value of the scale parameter.
If the distribution model of dist does not contain the dist_PARMINIT subroutine, then
 and all the nonscale distribution parameters are initialized to the default value of 0.001.
and all the nonscale distribution parameters are initialized to the default value of 0.001.
However, it is strongly recommended that each distribution’s model contain the dist_PARMINIT subroutine. See the section Defining a Distribution Model with the FCMP Procedure for more information. If that subroutine is defined, then
 is initialized as follows:
is initialized as follows:
Each input value
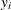 of the response variable is transformed to its scale-normalized version
of the response variable is transformed to its scale-normalized version 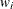 as
as
![\[ w_ i = \frac{y_ i}{\exp (\beta _0 + \sum _{j=1}^{k} \beta _ j x_{ij})} \]](images/etsug_severity0363.png)
where
 denotes the value of
denotes the value of 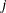 th regressor in the
th regressor in the 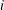 th input observation. These
th input observation. These 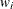 values are used to compute the input arguments for the dist_PARMINIT subroutine. The values that are computed by the subroutine for nonscale parameters are used as their respective
initial values. If the distribution has an untransformed scale parameter, then
values are used to compute the input arguments for the dist_PARMINIT subroutine. The values that are computed by the subroutine for nonscale parameters are used as their respective
initial values. If the distribution has an untransformed scale parameter, then  is set to the value of the scale parameter that is computed by the subroutine. If the distribution has a log-transformed
scale parameter
is set to the value of the scale parameter that is computed by the subroutine. If the distribution has a log-transformed
scale parameter  , then
, then  is computed as
is computed as  , where
, where  is the value of
is the value of  computed by the subroutine.
computed by the subroutine.
-
The value of
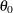 is initialized as
is initialized as
![\[ \theta _0 = s_0 \cdot \exp (\beta _0) \]](images/etsug_severity0368.png)
-
Reporting Estimates of Regression Parameters
When you request estimates to be written to the output (either ODS displayed output or in the OUTEST= data set), the estimate
of the base value of the first distribution parameter is reported. If the first parameter is the log-transformed scale parameter,
then the estimate of ![]() is reported; otherwise, the estimate of
is reported; otherwise, the estimate of ![]() is reported. The transform of the first parameter of a distribution dist is controlled by the dist_SCALETRANSFORM function that is defined for it.
is reported. The transform of the first parameter of a distribution dist is controlled by the dist_SCALETRANSFORM function that is defined for it.
CDF and PDF Estimates with Regression Effects
When regression effects are estimated, the estimate of the scale parameter depends on the values of the regressors and the estimates of the regression parameters. This dependency results in a potentially different distribution for each observation. To make estimates of the cumulative distribution function (CDF) and probability density function (PDF) comparable across distributions and comparable to the empirical distribution function (EDF), PROC SEVERITY reports the CDF and PDF estimates from a representative distribution. The representative distribution is a mixture of a certain number of distributions, where each distribution differs only in the value of the scale parameter. You can specify the number of distributions in the mixture and how their scale values are chosen by using the DFMIXTURE= option in the SCALEMODEL statement.
Let ![]() denote the number of observations used for estimation,
denote the number of observations used for estimation, ![]() denote the number of components in the mixture distribution,
denote the number of components in the mixture distribution, ![]() denote the scale parameter of the
denote the scale parameter of the ![]() th mixture component, and
th mixture component, and ![]() denote the weight associated with
denote the weight associated with ![]() th mixture component.
th mixture component.
Let ![]() and
and ![]() denote the PDF and CDF, respectively, of the
denote the PDF and CDF, respectively, of the ![]() th component distribution, where
th component distribution, where ![]() denotes the set of estimates of all parameters of the distribution other than the scale parameter. Then, the PDF and CDF
estimates,
denotes the set of estimates of all parameters of the distribution other than the scale parameter. Then, the PDF and CDF
estimates, ![]() and
and ![]() , respectively, of the mixture distribution at
, respectively, of the mixture distribution at ![]() are computed as follows:
are computed as follows:
|
|
|
|
|
|
where ![]() is the normalization factor (
is the normalization factor (![]() ).
).
The CDF estimates reported in OUTCDF= data set, plotted in CDF plots, and used for computing the EDF-based statistics of fit
are the ![]() values. The PDF estimates plotted in PDF plots are the
values. The PDF estimates plotted in PDF plots are the ![]() values.
values.
The scale values ![]() for the
for the ![]() mixture components are derived from the set
mixture components are derived from the set ![]() (
(![]() ) of
) of ![]() scale values, where
scale values, where ![]() denotes the estimate of the scale parameter due to observation
denotes the estimate of the scale parameter due to observation ![]() . It is computed as
. It is computed as
|
|
where ![]() is an estimate of the base value of the scale parameter,
is an estimate of the base value of the scale parameter, ![]() are the estimates of regression coefficients, and
are the estimates of regression coefficients, and ![]() is the value of regressor
is the value of regressor ![]() in observation
in observation ![]() .
.
Let ![]() denote the weight of observation
denote the weight of observation ![]() . If the WEIGHT statement is specified, then it is equal to the value of the specified weight variable for the corresponding
observation in the DATA= data set; otherwise, it is set to 1.
. If the WEIGHT statement is specified, then it is equal to the value of the specified weight variable for the corresponding
observation in the DATA= data set; otherwise, it is set to 1.
You can specify one of the following method-names in the DFMIXTURE= option in the SCALEMODEL statement to specify the method of choosing ![]() and the corresponding
and the corresponding ![]() and
and ![]() values:
values:
- FULL
-
In this method, there are as many mixture components as the number of observations that are used for estimation. In other words,
 ,
,  , and
, and  (
( ). This is the slowest method, because it requires
). This is the slowest method, because it requires  computations to compute the mixture CDF
computations to compute the mixture CDF  or the mixture PDF
or the mixture PDF  of one observation. For
of one observation. For 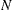 observations, the computational complexity in terms of number of PDF or CDF evaluations is
observations, the computational complexity in terms of number of PDF or CDF evaluations is  . Even for moderately large values of
. Even for moderately large values of 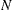 , the time taken to compute the mixture CDF and PDF can significantly exceed the time taken to estimate the model parameters.
So, it is recommended that you use this method only for small data sets.
, the time taken to compute the mixture CDF and PDF can significantly exceed the time taken to estimate the model parameters.
So, it is recommended that you use this method only for small data sets.
- MEAN
-
In this method, the mixture contains only one distribution, whose scale value is the mean of the scale values that are implied by all the observations. In other words,
 is computed as
is computed as
![\[ s_1 = \frac{1}{W} \sum _{i=1}^{N} w_ i \hat{\theta }_ i \]](images/etsug_severity0399.png)
where
 is the total weight (
is the total weight ( ).
).
This method is the fastest because it requires only one CDF or PDF evaluation per observation. The computational complexity is
 for
for 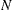 observations.
observations.
If you do not specify the DFMIXTURE= option in the SCALEMODEL statement, then this is the default method.
- QUANTILE
-
In this method, a certain number of quantiles are chosen from the set of all scale values. If you specify a value of
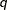 for the K= option when specifying this method, then
for the K= option when specifying this method, then  and
and  are set to be the
are set to be the 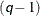
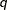 -quantiles from the set
-quantiles from the set  (
( ). The weight of each of the components (
). The weight of each of the components ( ) is assumed to be 1 for this method.
) is assumed to be 1 for this method.
The default value of
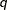 is 2, which implies a one-point mixture with a distribution whose scale value is equal to the median scale value.
is 2, which implies a one-point mixture with a distribution whose scale value is equal to the median scale value.
For this method, PROC SEVERITY needs to sort the
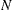 scale values in the set
scale values in the set  , which requires
, which requires  computations. Then, computing mixture estimate of one observation requires
computations. Then, computing mixture estimate of one observation requires 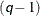 CDF or PDF evaluations. Hence, the computational complexity of this method is
CDF or PDF evaluations. Hence, the computational complexity of this method is  for computing a mixture PDF or CDF of
for computing a mixture PDF or CDF of 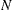 observations. For
observations. For  , it is significantly faster than the FULL method.
, it is significantly faster than the FULL method.
- RANDOM
-
In this method, a uniform random sample of observations is chosen and the mixture contains the distributions that are implied by those observations. If you specify a value of
 for the K= option when specifying this method, then the size of the sample is
for the K= option when specifying this method, then the size of the sample is  . Hence,
. Hence,  . If
. If  denotes the index of
denotes the index of 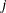 th observation in the sample (
th observation in the sample ( ), such that
), such that  , then the scale of
, then the scale of 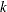 th component distribution in the mixture is
th component distribution in the mixture is  and the weight associated with it is
and the weight associated with it is  .
.
You can also specify the seed to be used for generating the random sample by using the SEED= option for this method. The same sample of observations is used for all models.
Computing a mixture estimate of one observation requires
 CDF or PDF evaluations. Hence, the computational complexity of this method is
CDF or PDF evaluations. Hence, the computational complexity of this method is  for computing a mixture PDF or CDF of
for computing a mixture PDF or CDF of 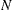 observations. For
observations. For  , it is significantly faster than the FULL method.
, it is significantly faster than the FULL method.