The VARMAX Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing Values VARMAX Model Dynamic Simultaneous Equations Modeling Impulse Response Function Forecasting Tentative Order Selection VAR and VARX Modeling Bayesian VAR and VARX Modeling VARMA and VARMAX Modeling Model Diagnostic Checks Cointegration Vector Error Correction Modeling I(2) Model Multivariate GARCH Modeling Output Data Sets OUT= Data Set OUTEST= Data Set OUTHT= Data Set OUTSTAT= Data Set Printed Output ODS Table Names ODS Graphics Computational Issues
Missing Values VARMAX Model Dynamic Simultaneous Equations Modeling Impulse Response Function Forecasting Tentative Order Selection VAR and VARX Modeling Bayesian VAR and VARX Modeling VARMA and VARMAX Modeling Model Diagnostic Checks Cointegration Vector Error Correction Modeling I(2) Model Multivariate GARCH Modeling Output Data Sets OUT= Data Set OUTEST= Data Set OUTHT= Data Set OUTSTAT= Data Set Printed Output ODS Table Names ODS Graphics Computational Issues -
Examples

- References
| Bayesian Vector Error Correction Model |
Bayesian inference on a cointegrated system begins by using the priors of 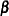 obtained from the VECM(
obtained from the VECM(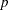 ) form. Bayesian vector error correction models can improve forecast accuracy for cointegrated processes.
) form. Bayesian vector error correction models can improve forecast accuracy for cointegrated processes.
The following statements fit a BVECM(2) form to the simulated data. You specify both the PRIOR= and ECM= options for the Bayesian vector error correction model. The VARMAX procedure output is shown in Figure 35.17.
/*--- Bayesian Vector Error-Correction Model ---*/
proc varmax data=simul2;
model y1 y2 / p=2 noint
prior=( lambda=0.5 theta=0.2 )
ecm=( rank=1 normalize=y1 )
print=(estimates);
run;
Figure 35.17 shows the model type fitted to the data, the estimates of the adjustment coefficient ( ), the parameter estimates in terms of lag one coefficients (
), the parameter estimates in terms of lag one coefficients (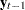 ), and lag one first differenced coefficients (
), and lag one first differenced coefficients ( ).
).
Figure 35.17
Parameter Estimates for the BVECM(2) Form
The VARMAX Procedure
| Type of Model | BVECM(2) |
|---|---|
| Estimation Method | Maximum Likelihood Estimation |
| Cointegrated Rank | 1 |
| Prior Lambda | 0.5 |
| Prior Theta | 0.2 |
| Alpha | |
|---|---|
| Variable | 1 |
| y1 | -0.34392 |
| y2 | 0.16659 |
| Parameter Alpha * Beta' Estimates | ||
|---|---|---|
| Variable | y1 | y2 |
| y1 | -0.34392 | 0.67262 |
| y2 | 0.16659 | -0.32581 |
| AR Coefficients of Differenced Lag | |||
|---|---|---|---|
| DIF Lag | Variable | y1 | y2 |
| 1 | y1 | -0.80070 | -0.59320 |
| y2 | 0.33417 | -0.53480 | |