The UCM Procedure
- Overview
-
Getting Started

-
Syntax
 Functional Summary PROC UCM Statement AUTOREG Statement BLOCKSEASON Statement BY Statement CYCLE Statement DEPLAG Statement ESTIMATE Statement FORECAST Statement ID Statement IRREGULAR Statement LEVEL Statement MODEL Statement NLOPTIONS Statement OUTLIER Statement RANDOMREG Statement SEASON Statement SLOPE Statement SPLINEREG Statement SPLINESEASON Statement
Functional Summary PROC UCM Statement AUTOREG Statement BLOCKSEASON Statement BY Statement CYCLE Statement DEPLAG Statement ESTIMATE Statement FORECAST Statement ID Statement IRREGULAR Statement LEVEL Statement MODEL Statement NLOPTIONS Statement OUTLIER Statement RANDOMREG Statement SEASON Statement SLOPE Statement SPLINEREG Statement SPLINESEASON Statement -
Details

-
Examples

- References
Example 34.3 Modeling Long Seasonal Patterns
This example illustrates some of the techniques you can use to model long seasonal patterns in a series. If the seasonal pattern is of moderate length and the underlying dynamics are simple, then it is easily modeled by using the basic settings of the SEASON statement and these additional techniques are not needed. However, if the seasonal pattern has a long season length and/or has a complex stochastic dynamics, then the techniques discussed here can be useful. You can obtain parsimonious models for a long seasonal pattern by using an appropriate subset of trigonometric harmonics, or by using a suitable spline function, or by using a block-season pattern in combination with a seasonal component of much smaller length. You can also vary the disturbance variances of the subcomponents that combine to form the seasonal component.
The time series used in this example consists of number of calls received per shift at a call center. Each shift is six hours long, and the first shift of the day begins at midnight, resulting in four shifts per day. The observations are available from December 15, 1999, to April 30, 2000. This series is seasonal with season length 28, which is moderate, and in fact there is no particular need to use pattern approximation techniques in this case. However, it is adequate for demonstration purposes. The plan of this example is as follows. First an initial model with a full seasonal component is created. This model is used as a baseline for comparing alternate models created by the techniques that are being illustrated. In practice any candidate model is first checked for adequacy by using various diagnostic procedures. In this illustration the main focus is on the different ways a long seasonal pattern can be modeled and no model diagnostics are done for the models being entertained. The alternate models are compared by using the sum of absolute prediction errors in the holdout region.
The following DATA step statements create the input data set used in this example.
data callCenter; input calls @@; label calls= "Number of Calls Received in a 6 Hour Shift"; start = '15dec99:00:00'dt; datetime = INTNX( 'dthour6', start, _n_-1 ); format datetime datetime10.; datalines; 18 122 244 128 19 113 230 119 17 112 219 93 14 73 139 53 11 32 74 56 15 137 289 153 20 125 227 106 16 101 ... more lines ...
Initial exploration of the series clearly indicates that the series does not show any significant trend, and time of day and day of the week have a significant influence on the number of calls received. These considerations suggest a simple random walk trend model along with a seasonal component of season length 28, the total number of shifts in a week. The following statements specify this model. Note the PRINT=HARMONICS option in the SEASON statement, which produces a table that lists the full set of harmonics contributing to the seasonal along with the significance of their contribution. This table will be useful later in choosing a subset trigonometric model. The BACK=28 and the LEAD=28 specifications in the FORECAST statement create a holdout region of 28 observations. The sum of absolute prediction errors (SAE) in this holdout region are used to compare the different models.
proc ucm data=callCenter;
id datetime interval=dthour6;
model calls;
irregular;
level;
season length=28 type=trig
print=(harmonics);
estimate back=28;
forecast back=28 lead=28;
run;
The forecasting performance of this model in the holdout region is shown in Output 34.3.1. The sum of absolute prediction errors SAE = 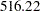 , which appears in the last row of the holdout analysis table.
, which appears in the last row of the holdout analysis table.
| Obs | datetime | Actual | Forecast | Error | SAE |
|---|---|---|---|---|---|
| 525 | 24APR00:00 | 12 | -4.004 | 16.004 | 16.004 |
| 526 | 24APR00:06 | 136 | 110.825 | 25.175 | 41.179 |
| 527 | 24APR00:12 | 295 | 262.820 | 32.180 | 73.360 |
| 528 | 24APR00:18 | 172 | 145.127 | 26.873 | 100.232 |
| 529 | 25APR00:00 | 20 | 2.188 | 17.812 | 118.044 |
| 530 | 25APR00:06 | 127 | 105.442 | 21.558 | 139.602 |
| 531 | 25APR00:12 | 236 | 217.043 | 18.957 | 158.559 |
| 532 | 25APR00:18 | 125 | 114.313 | 10.687 | 169.246 |
| 533 | 26APR00:00 | 16 | 2.855 | 13.145 | 182.391 |
| 534 | 26APR00:06 | 108 | 95.202 | 12.798 | 195.189 |
| 535 | 26APR00:12 | 207 | 194.184 | 12.816 | 208.005 |
| 536 | 26APR00:18 | 112 | 97.687 | 14.313 | 222.317 |
| 537 | 27APR00:00 | 15 | 1.270 | 13.730 | 236.047 |
| 538 | 27APR00:06 | 98 | 85.875 | 12.125 | 248.172 |
| 539 | 27APR00:12 | 200 | 184.891 | 15.109 | 263.281 |
| 540 | 27APR00:18 | 113 | 93.113 | 19.887 | 283.168 |
| 541 | 28APR00:00 | 15 | -1.120 | 16.120 | 299.288 |
| 542 | 28APR00:06 | 104 | 84.983 | 19.017 | 318.305 |
| 543 | 28APR00:12 | 205 | 177.940 | 27.060 | 345.365 |
| 544 | 28APR00:18 | 89 | 64.292 | 24.708 | 370.073 |
| 545 | 29APR00:00 | 12 | -6.020 | 18.020 | 388.093 |
| 546 | 29APR00:06 | 68 | 46.286 | 21.714 | 409.807 |
| 547 | 29APR00:12 | 116 | 100.339 | 15.661 | 425.468 |
| 548 | 29APR00:18 | 54 | 34.700 | 19.300 | 444.768 |
| 549 | 30APR00:00 | 10 | -6.209 | 16.209 | 460.978 |
| 550 | 30APR00:06 | 30 | 12.167 | 17.833 | 478.811 |
| 551 | 30APR00:12 | 66 | 49.524 | 16.476 | 495.287 |
| 552 | 30APR00:18 | 61 | 40.071 | 20.929 | 516.216 |
Now that a baseline model is created, the exploration for alternate models can begin. The review of the harmonic table in Output 34.3.2 shows that all but the last three harmonics are significant, and deleting any of them to form a subset trigonometric seasonal component will lead to a poorer model. The last three harmonics, 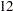 th,
th,  th and
th and 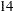 th, with periods of 2.333, 2.15 and 2.0, respectively, do appear to be possible choices for deletion. Note that the disturbance variance of the seasonal component is not very insignificant (see Output 34.3.3); therefore the seasonal component is stochastic and the preceding logic, which is based on the final state estimate, provides only a rough guideline.
th, with periods of 2.333, 2.15 and 2.0, respectively, do appear to be possible choices for deletion. Note that the disturbance variance of the seasonal component is not very insignificant (see Output 34.3.3); therefore the seasonal component is stochastic and the preceding logic, which is based on the final state estimate, provides only a rough guideline.
| Harmonic Analysis of Trigonometric Seasons (Based on the Final State) | ||||||
|---|---|---|---|---|---|---|
| Name | Season Length | Harmonic | Period | Chi-Square | DF | Pr > ChiSq |
| Season | 28 | 1 | 28.00000 | 234.19 | 2 | <.0001 |
| Season | 28 | 2 | 14.00000 | 264.19 | 2 | <.0001 |
| Season | 28 | 3 | 9.33333 | 95.65 | 2 | <.0001 |
| Season | 28 | 4 | 7.00000 | 105.64 | 2 | <.0001 |
| Season | 28 | 5 | 5.60000 | 146.74 | 2 | <.0001 |
| Season | 28 | 6 | 4.66667 | 121.93 | 2 | <.0001 |
| Season | 28 | 7 | 4.00000 | 4299.12 | 2 | <.0001 |
| Season | 28 | 8 | 3.50000 | 150.79 | 2 | <.0001 |
| Season | 28 | 9 | 3.11111 | 89.68 | 2 | <.0001 |
| Season | 28 | 10 | 2.80000 | 8.95 | 2 | 0.0114 |
| Season | 28 | 11 | 2.54545 | 6.14 | 2 | 0.0464 |
| Season | 28 | 12 | 2.33333 | 2.20 | 2 | 0.3325 |
| Season | 28 | 13 | 2.15385 | 3.40 | 2 | 0.1828 |
| Season | 28 | 14 | 2.00000 | 2.33 | 1 | 0.1272 |
| Final Estimates of the Free Parameters | |||||
|---|---|---|---|---|---|
| Component | Parameter | Estimate | Approx Std Error |
t Value | Approx Pr > |t| |
| Irregular | Error Variance | 92.14591 | 13.10986 | 7.03 | <.0001 |
| Level | Error Variance | 44.83595 | 10.65465 | 4.21 | <.0001 |
| Season | Error Variance | 0.01250 | 0.0065153 | 1.92 | 0.0551 |
The following statements fit a subset trigonometric model formed by dropping the last three harmonics by specifying the DROPH= option in the SEASON statement:
proc ucm data=callCenter; id datetime interval=dthour6; model calls; irregular; level; season length=28 type=trig droph=12 13 14; estimate back=28; forecast back=28 lead=28; run;
The last row of the holdout region prediction analysis table for the preceding model is shown in Output 34.3.4. It shows that the subset trigonometric model has better prediction performance in the holdout region than the full trigonometric model, its SAE =  compared to the SAE =
compared to the SAE = 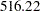 for the full model.
for the full model.
| Obs | datetime | Actual | Forecast | Error | SAE |
|---|---|---|---|---|---|
| 552 | 30APR00:18 | 61 | 40.836 | 20.164 | 471.534 |
The following statements illustrate a spline approximation to this seasonal component. In the spline specification the knot placement is quite important, and usually some experimentation is needed. In the following model the knots are placed at the beginning and the middle of each day. Note that the knots at the beginning and end of the season, 1 and 28 in this case, should not be listed in the knot list because knots are always placed there anyway.
proc ucm data=callCenter;
id datetime interval=dthour6;
model calls;
irregular;
level;
splineseason length=28
knots=3 5 7 9 11 13 15 17 19 21 23 25 27
degree=3;
estimate back=28;
forecast back=28 lead=28;
run;
The spline season model takes about half the time to fit that the baseline model takes. The last row of the holdout region prediction analysis table for this model is shown in Output 34.3.5, which shows that the spline season model performs even better than the previous two models in the holdout region, its SAE =  compared to SAE =
compared to SAE =  for the previous model.
for the previous model.
| Obs | datetime | Actual | Forecast | Error | SAE |
|---|---|---|---|---|---|
| 552 | 30APR00:18 | 61 | 23.350 | 37.650 | 313.792 |
The following statements illustrate yet another way to approximate a long seasonal component. Here a combination of BLOCKSEASON and SEASON statements results in a seasonal component that is a sum of two seasonal patterns: one seasonal pattern is simply a regular season with season length 4 that captures the within-day seasonal pattern, and the other seasonal pattern is a block seasonal pattern that remains constant during the day but varies from day to day within a week. Note the use of NLOPTIONS statement to change the optimization technique during the parameter estimation to DBLDOG, which in this case performs better than the default technique, TRUREG.
proc ucm data=callCenter;
id datetime interval=dthour6;
model calls;
irregular;
level;
season length=4 type=trig;
blockseason nblocks=7 blocksize=4
type=trig;
estimate back=28;
forecast back=28 lead=28;
nloptions tech=dbldog;
run;
This model also takes about half the time to fit that the baseline model takes. The last row of the holdout region prediction analysis table for this model is shown in Output 34.3.6, which shows that the block season model does slightly better than the baseline model but not as good as the other two models, its SAE = 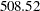 compared to the SAE =
compared to the SAE = 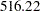 of the baseline model.
of the baseline model.
| Obs | datetime | Actual | Forecast | Error | SAE |
|---|---|---|---|---|---|
| 552 | 30APR00:18 | 61 | 39.339 | 21.661 | 508.522 |
This example showed a few different ways to model a long seasonal pattern. It showed that parsimonious models for long seasonal patterns can be useful, and in some cases even more effective than the full model. Moreover, for very long seasonal patterns the high memory requirements and long computing times might make full models impractical.