The SSM Procedure (Experimental)
-
Overview

- Getting Started
-
Syntax

-
Details
 The State Space Model and Notation Types of Data Organization Overview of Model Specification Syntax Likelihood, Filtering, and Smoothing Contrasting PROC SSM with Other SAS Procedures Predefined Trend Models Predefined Structural Models Covariance Parameterization Missing Values Computational Issues Displayed Output ODS Table Names OUT= Data Set
The State Space Model and Notation Types of Data Organization Overview of Model Specification Syntax Likelihood, Filtering, and Smoothing Contrasting PROC SSM with Other SAS Procedures Predefined Trend Models Predefined Structural Models Covariance Parameterization Missing Values Computational Issues Displayed Output ODS Table Names OUT= Data Set -
Examples

- References
| TREND Statement |
- TREND name ( type ) <options> ;
Some of these trend specifications are applicable to all the data types—that is, they can be used for regular data types in addition to irregular data types, while the others require that the data be regular or regular-with-replication. Of course, the trend specification is only a part of the overall model specification. Therefore, the other parts of the model can imply additional constraints on the data type.
Table 27.3 lists the available trend models and their data requirements. The "type" column shows the admissible keywords that signify the particular trend type. For brevity, the "Data Type" column in Table 27.3 groups the regular and regular-with-replication data types into one category—regular. The section Predefined Trend Models provides additional details about these trend models.
type |
Data Type |
Description |
Parameters |
|---|---|---|---|
RW |
Regular |
Random walk |
Level |
LL |
Regular |
Local linear |
Level and slope |
DLL |
Regular |
Damped local linear |
Level and slope |
damping factor |
|||
PS(order) |
Irregular |
Polynomial spline of order up to 3 |
Level |
DECAY |
Irregular |
A type of decay pattern |
Level |
DECAY(OU) |
Irregular |
Ornstein-Uhlenbeck decay pattern |
Level |
GROWTH |
Irregular |
A type of growth pattern |
Level |
GROWTH(OU) |
Irregular |
Ornstein-Uhlenbeck growth pattern |
Level |
The following example specifies polySpline as a trend of type polynomial spline of order 2:
trend polySpline(ps(2));
Similarly, the following statement defines dampedTrend as a damped local linear trend:
trend dampedTrend(dll) slopevar=x;
The variance parameter that governs the slope equation of this trend type is given by a variable x, which must be defined elsewhere in the program. The other parameters that define dampedTrend are left unspecified.
- CROSS=(var1, var2, ...)
-
creates a linear combination of one or more independent trend components based on the variables in the list. If the parameters of the trend are specified by options such as the LEVELVAR= option or the PHI= option, these parameters are shared by these constituent trends. For example, suppose that the CROSS= list contains two variables
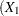 and
and 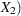 and the trend specification is of the type RW. The effect of CROSS=(
and the trend specification is of the type RW. The effect of CROSS=(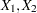 ) is to create a component
) is to create a component 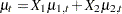 where
where 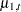 and
and 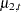 are two independent random walk trends. Moreover, if the random walk trend specification uses the LEVELVAR= option to specify the variance parameter,
are two independent random walk trends. Moreover, if the random walk trend specification uses the LEVELVAR= option to specify the variance parameter, 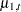 and
and 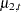 share the same variance parameter; otherwise, two separate variance parameters are assigned to these random walks. The CROSS= option is useful for a variety of situations. For example, suppose
share the same variance parameter; otherwise, two separate variance parameters are assigned to these random walks. The CROSS= option is useful for a variety of situations. For example, suppose 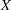 is an indicator variable that is 1 before certain time point
is an indicator variable that is 1 before certain time point 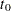 and 0 thereafter; CROSS=(X) has the effect of turning off the trend component after time
and 0 thereafter; CROSS=(X) has the effect of turning off the trend component after time 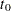 . Similarly, suppose
. Similarly, suppose 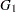 and
and 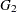 are indicators for gender—for example,
are indicators for gender—for example, 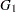 = (GENDER="M") and
= (GENDER="M") and 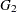 = (GENDER="F"). Then CROSS=(
= (GENDER="F"). Then CROSS=(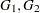 ) creates a trend that varies with the gender of the observation. The variables in the CROSS= list must be free of unknown parameters.
) creates a trend that varies with the gender of the observation. The variables in the CROSS= list must be free of unknown parameters. The CROSS= option can be computationally expensive; computationally it is equivalent to specifying as many separate trends as the number of variables in the specified list.
- LEVELVAR=variable | number
specifies the disturbance variance parameter for all the trend types. For trend types LL and DLL, this option specifies
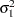 . Any nonnegative value, including zero, is permissible. If variable contains unknown parameters, they are estimated from the data. Similarly, if the LEVELVAR= option is not specified,
. Any nonnegative value, including zero, is permissible. If variable contains unknown parameters, they are estimated from the data. Similarly, if the LEVELVAR= option is not specified, 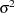 is estimated from the data.
is estimated from the data. - PHI=variable | number
specifies the value of
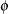 for trend types DLL, DECAY, DECAY(OU), GROWTH, and GROWTH(OU). For the type DLL, the specified value must be between 0.0 and 1.0. For types DECAY and DECAY(OU),
for trend types DLL, DECAY, DECAY(OU), GROWTH, and GROWTH(OU). For the type DLL, the specified value must be between 0.0 and 1.0. For types DECAY and DECAY(OU), 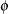 must be strictly negative. For types GROWTH and GROWTH(OU),
must be strictly negative. For types GROWTH and GROWTH(OU), 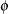 must be strictly positive. If variable contains unknown parameters, they are estimated from the data. Similarly, if the PHI= option is not specified,
must be strictly positive. If variable contains unknown parameters, they are estimated from the data. Similarly, if the PHI= option is not specified, 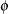 is estimated from the data.
is estimated from the data. - SLOPEVAR=variable | number
specifies the second disturbance variance parameter,
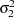 , for trend types LL and DLL. Any nonnegative value, including zero, is permissible. If variable contains unknown parameters, they are estimated from the data. Similarly, if the SLOPEVAR= option is not specified,
, for trend types LL and DLL. Any nonnegative value, including zero, is permissible. If variable contains unknown parameters, they are estimated from the data. Similarly, if the SLOPEVAR= option is not specified, 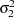 is estimated from the data.
is estimated from the data.
Note: This procedure is experimental.
