Example 20.5 Using the FLATDATA Statement
Sometimes the data can be found in compressed form, where each line consists of all observations for the dependent and independent variables for the cross section. To illustrate, suppose you have a data set with 20 cross sections where each cross section consists of observations for six time periods. Each time period has values for dependent and independent variables 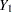 ...
...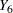 and
and 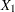 ...
...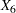 . The
. The 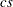 and
and 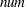 variables represent other character and numeric variables that are constant across each cross section.
variables represent other character and numeric variables that are constant across each cross section.
The observations for first five cross sections along with other variables are shown in Output 20.5.1. In this example,  represents the cross section. The time period is identified by the subscript on the
represents the cross section. The time period is identified by the subscript on the 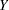 and
and 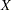 variables; it ranges from 1 to 6.
variables; it ranges from 1 to 6.
Output 20.5.1
Compressed Data Set
| 1 |
CS1 |
-1.56058 |
0.40268 |
0.91951 |
0.69482 |
-2.28899 |
-1.32762 |
1.92348 |
2.30418 |
2.11850 |
2.66009 |
-4.94104 |
-0.83053 |
5.01359 |
| 2 |
CS2 |
0.30989 |
1.01950 |
-0.04699 |
-0.96695 |
-1.08345 |
-0.05180 |
0.30266 |
4.50982 |
3.73887 |
1.44984 |
-1.02996 |
2.78260 |
1.73856 |
| 3 |
CS3 |
0.85054 |
0.60325 |
0.71154 |
0.66168 |
-0.66823 |
-1.87550 |
0.55065 |
4.07276 |
4.89621 |
3.90470 |
1.03437 |
0.54598 |
5.01460 |
| 4 |
CS4 |
-0.18885 |
-0.64946 |
-1.23355 |
0.04554 |
-0.24996 |
0.09685 |
-0.92771 |
2.40304 |
1.48182 |
2.70579 |
3.82672 |
4.01117 |
1.97639 |
| 5 |
CS5 |
-0.04761 |
-0.79692 |
0.63445 |
-2.23539 |
-0.37629 |
-0.82212 |
-0.70566 |
3.58092 |
6.08917 |
3.08249 |
4.26605 |
3.65452 |
0.81826 |
Since the PANEL procedure cannot work directly with the data in compressed form, the FLATDATA statement can be used to transform the data. The OUT= option can be used to output transformed data to a data set.
proc panel data=flattest;
flatdata indid=i tsname="t" base=(X Y)
keep=( cs num seed ) / out=flat_out;
id i t;
model y = x / fixone noint;
run;
First, six observations for the uncompressed data set and results for the one-way fixed-effects model fitted are shown in Output 20.5.2 and Output 20.5.3.
Output 20.5.2
Uncompressed Data Set
| 1 |
1 |
0.40268 |
2.30418 |
CS1 |
-1.56058 |
| 1 |
2 |
0.91951 |
2.11850 |
CS1 |
-1.56058 |
| 1 |
3 |
0.69482 |
2.66009 |
CS1 |
-1.56058 |
| 1 |
4 |
-2.28899 |
-4.94104 |
CS1 |
-1.56058 |
| 1 |
5 |
-1.32762 |
-0.83053 |
CS1 |
-1.56058 |
| 1 |
6 |
1.92348 |
5.01359 |
CS1 |
-1.56058 |
Output 20.5.3
Estimation with the FLATDATA Statement
The PANEL Procedure
Fixed One Way Estimates
Dependent Variable: Y
| 1 |
0.945589 |
0.4579 |
2.06 |
0.0416 |
Cross Sectional Effect 1 |
| 1 |
2.475449 |
0.4582 |
5.40 |
<.0001 |
Cross Sectional Effect 2 |
| 1 |
3.250337 |
0.4579 |
7.10 |
<.0001 |
Cross Sectional Effect 3 |
| 1 |
3.712149 |
0.4617 |
8.04 |
<.0001 |
Cross Sectional Effect 4 |
| 1 |
5.023584 |
0.4661 |
10.78 |
<.0001 |
Cross Sectional Effect 5 |
| 1 |
6.791074 |
0.4707 |
14.43 |
<.0001 |
Cross Sectional Effect 6 |
| 1 |
6.11374 |
0.4649 |
13.15 |
<.0001 |
Cross Sectional Effect 7 |
| 1 |
8.733843 |
0.4580 |
19.07 |
<.0001 |
Cross Sectional Effect 8 |
| 1 |
8.916685 |
0.4587 |
19.44 |
<.0001 |
Cross Sectional Effect 9 |
| 1 |
8.913916 |
0.4614 |
19.32 |
<.0001 |
Cross Sectional Effect 10 |
| 1 |
10.82881 |
0.4580 |
23.64 |
<.0001 |
Cross Sectional Effect 11 |
| 1 |
11.40867 |
0.4603 |
24.79 |
<.0001 |
Cross Sectional Effect 12 |
| 1 |
12.8865 |
0.4585 |
28.10 |
<.0001 |
Cross Sectional Effect 13 |
| 1 |
13.37819 |
0.4580 |
29.21 |
<.0001 |
Cross Sectional Effect 14 |
| 1 |
14.72619 |
0.4579 |
32.16 |
<.0001 |
Cross Sectional Effect 15 |
| 1 |
15.58813 |
0.4580 |
34.04 |
<.0001 |
Cross Sectional Effect 16 |
| 1 |
17.77983 |
0.4579 |
38.83 |
<.0001 |
Cross Sectional Effect 17 |
| 1 |
17.9909 |
0.4618 |
38.96 |
<.0001 |
Cross Sectional Effect 18 |
| 1 |
18.87283 |
0.4583 |
41.18 |
<.0001 |
Cross Sectional Effect 19 |
| 1 |
19.40034 |
0.4579 |
42.37 |
<.0001 |
Cross Sectional Effect 20 |
| 1 |
2.010753 |
0.1217 |
16.52 |
<.0001 |
|
Copyright © SAS Institute Inc. All rights reserved.


 Missing Values Computational Resources Restricted Estimates Notation The One-Way Fixed-Effects Model The Two-Way Fixed-Effects Model Balanced Panels Unbalanced Panels Between Estimators Pooled Estimator The One-Way Random-Effects Model The Two-Way Random-Effects Model Parks Method (Autoregressive Model) Da Silva Method (Variance-Component Moving Average Model) Dynamic Panel Estimator Linear Hypothesis Testing Heteroscedasticity-Corrected Covariance Matrices R Square Specification Tests Troubleshooting ODS Graphics The OUTPUT OUT= Data Set The OUTEST= Data Set The OUTTRANS= Data Set Printed Output ODS Table Names
Missing Values Computational Resources Restricted Estimates Notation The One-Way Fixed-Effects Model The Two-Way Fixed-Effects Model Balanced Panels Unbalanced Panels Between Estimators Pooled Estimator The One-Way Random-Effects Model The Two-Way Random-Effects Model Parks Method (Autoregressive Model) Da Silva Method (Variance-Component Moving Average Model) Dynamic Panel Estimator Linear Hypothesis Testing Heteroscedasticity-Corrected Covariance Matrices R Square Specification Tests Troubleshooting ODS Graphics The OUTPUT OUT= Data Set The OUTEST= Data Set The OUTTRANS= Data Set Printed Output ODS Table Names
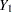 ...
...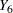 and
and 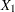 ...
...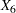 . The
. The 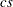 and
and 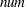 variables represent other character and numeric variables that are constant across each cross section.
variables represent other character and numeric variables that are constant across each cross section.  represents the cross section. The time period is identified by the subscript on the
represents the cross section. The time period is identified by the subscript on the 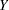 and
and 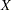 variables; it ranges from 1 to 6.
variables; it ranges from 1 to 6.