| The EXPAND Procedure |
| Transformation Operations |
The operations that can be used in the TRANSFORMIN= and TRANSFORMOUT= options are shown in Table 14.1. Operations are applied to each value of the series. Each value of the series is replaced by the result of the operation.
In Table 14.1, 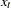 or x represents the value of the series at a particular time period t before the transformation is applied,
or x represents the value of the series at a particular time period t before the transformation is applied, 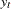 represents the value of the result series, and N represents the total number of observations.
represents the value of the result series, and N represents the total number of observations.
The notation [ n ] indicates that the argument n is optional; the default is 1. The notation window is used as the argument for the moving statistics operators, and it indicates that you can specify either an integer number of periods n or a list of n weights in parentheses. The notation sequence is used as the argument for the sequence operators, and it indicates that you must specify a sequence of numbers. The notation s indicates the length of seasonality, and it is a required argument.
Syntax |
Result |
|---|---|
+ number |
adds the specified number : |
- number |
subtracts the specified number : |
* number |
multiplies by the specified number : |
/ number |
divides by the specified number : |
ABS |
absolute value: |
ADJUST |
indicates that the following moving window summation or product operator should be adjusted for window width |
CD_I s |
classical decomposition irregular component |
CD_S s |
classical decomposition seasonal component |
CD_SA s |
classical decomposition seasonally adjusted series |
CD_TC s |
classical decomposition trend-cycle component |
CDA_I s |
classical decomposition (additive) irregular component |
CDA_S s |
classical decomposition (additive) seasonal component |
CDA_SA s |
classical decomposition (additive) seasonally adjusted series |
CEIL |
smallest integer greater than or equal to x : |
CMOVAVE window |
centered moving average |
CMOVCSS window |
centered moving corrected sum of squares |
CMOVGMEAN window |
centered moving geometric mean |
CMOVMAX n |
centered moving maximum |
CMOVMED n |
centered moving median |
CMOVMIN n |
centered moving minimum |
CMOVPROD window |
centered moving product |
CMOVRANGE n |
centered moving range |
CMOVRANK |
centered moving rank |
CMOVSTD window |
centered moving standard deviation |
CMOVSUM n |
centered moving sum |
CMOVTVALUE window |
centered moving t -value |
CMOVUSS window |
centered moving uncorrected sum of squares |
CMOVVAR window |
centered moving variance |
CUAVE [ n ] |
cumulative average |
CUCSS [ n ] |
cumulative corrected sum of squares |
CUGMEAN [ n ] |
cumulative geometric mean |
CUMAX [ n ] |
cumulative maximum |
CUMED [ n ] |
cumulative median |
CUMIN [ n ] |
cumulative minimum |
CUPROD [ n ] |
cumulative product |
CURANK [ n ] |
cumulative rank |
CURANGE [ n ] |
cumulative range |
CUSTD [ n ] |
cumulative standard deviation |
CUSUM [ n ] |
cumulative sum |
CUTVALUE [ n ] |
cumulative t -value |
CUUSS [ n ] |
cumulative uncorrected sum of squares |
CUVAR [ n ] |
cumulative variance |
DIF [ n ] |
span n difference: |
EWMA number |
exponentially weighted moving average of |
smoothing weight number, where |
|
|
|
This operation is also called simple exponential smoothing. |
|
EXP |
exponential function: |
FDIF d |
fractional difference with difference order d where |
FLOOR |
largest integer less than or equal to x : |
FSUM |
fractional summation with summation order d where |
HP_T lambda |
Hodrick-Prescott Filter trend component where lambda is the nonnegative filter parameter |
HP_C lambda |
Hodrick-Prescott Filter cycle component where lambda is the nonnegative filter parameter |
ILOGIT |
inverse logistic function: |
LAG [ n ] |
value of the series n periods earlier: |
LEAD [ n ] |
value of the series n periods later: |
LOG |
natural logarithm: |
LOGIT |
logistic function: |
MAX number |
maximum of x and number : |
MIN number |
minimum of x and number : |
> number |
missing value if |
>= number |
missing value if |
= number |
missing value if |
|
missing value if |
< number |
missing value if |
<= number |
missing value if |
MOVAVE n |
backward moving average of n neighboring values: |
|
|
MOVAVE window |
backward weighted moving average of neighboring values: |
|
|
MOVCSS window |
backward moving corrected sum of squares |
MOVGMEAN window |
backward moving geometric mean |
MOVMAX n |
backward moving maximum |
MOVMED n |
backward moving median |
MOVMIN n |
backward moving minimum |
MOVPROD window |
backward moving product |
MOVRANGE n |
backward moving range |
MOVRANK |
backward moving rank |
MOVSTD window |
backward moving standard deviation |
MOVSUM n |
backward moving sum |
MOVTVALUE window |
backward moving t-value |
MOVUSS window |
backward moving uncorrected sum of squares |
MOVVAR window |
backward moving variance |
MISSONLY <MEAN> |
indicates that the following moving time window |
statistic operator should replace only missing values with the |
|
moving statistic and should leave nonmissing values unchanged. |
|
If the option MEAN is specified, then missing values are |
|
replaced by the overall mean of the series. |
|
NEG |
changes the sign: |
NOMISS |
indicates that the following moving time window |
statistic operator should not allow missing values |
|
PCTDIF |
percent difference of the current value and lag n |
PCTSUM |
percent summation of the current value and cumulative sum |
RATIO |
ratio of current value to lag |
RECIPROCAL |
reciprocal: |
REVERSE |
reverse the series: |
SCALE |
scale series between |
SEQADD sequence |
add sequence values to series |
SEQDIV sequence |
divide series by sequence values |
SEQMINUS sequence |
subtract sequence values to series |
SEQMULT sequence |
multiply series by sequence values |
SET |
set all values of |
SETEMBEDDED |
set embedded values of |
SETLEFT |
set beginning values of |
SETMISS number |
replaces missing values in the series with the number specified |
SETRIGHT |
set ending values of |
SIGN |
-1, 0, or 1 as x is < 0, equals 0, or > 0 respectively |
SQRT |
square root: |
SQUARE |
square: |
SUM |
cumulative sum: |
SUM n |
cumulative sum of multiples of n-period lags: |
|
|
TRIM n |
sets |
TRIMLEFT n |
sets |
TRIMRIGHT n |
sets |
Moving Time Window Operators
Some operators compute statistics for a set of values within a moving time window; these are called moving time window operators. There are centered and backward versions of these operators.
The centered moving time window operators are CMOVAVE, CMOVCSS, CMOVGMEAN, CMOVMAX, CMOVMED, CMOVMIN, CMOVPROD, CMOVRANGE, CMOVRANK, CMOVSTD, CMOVSUM, CMOVTVALUE, CMOVUSS, and CMOVVAR. These operators compute statistics of the  values
values 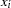 for observations
for observations 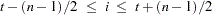 .
.
The backward moving time window operators are MOVAVE, MOVCSS, MOVGMEAN, MOVMAX, MOVMED, MOVMIN, MOVPROD, MOVRANGE, MOVRANK, MOVSTD, MOVSUM, MOVTVALUE, MOVUSS, and MOVVAR. These operators compute statistics of the  values
values 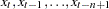 .
.
All the moving time window operators accept an argument  specifying the number of periods to include in the time window. For example, the following statement computes a five-period backward moving average of X.
specifying the number of periods to include in the time window. For example, the following statement computes a five-period backward moving average of X.
convert x=y / transformout=( movave 5 );
In this example, the resulting transformation is
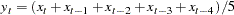 |
The following statement computes a five-period centered moving average of X.
convert x=y / transformout=( cmovave 5 );
In this example, the resulting transformation is
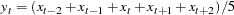 |
If the window with a centered moving time window operator is not an odd number, one more lagged value than lead value is included in the time window. For example, the result of the CMOVAVE 4 operator is
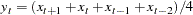 |
You can compute a forward moving time window operation by combining a backward moving time window operator with the REVERSE operator. For example, the following statement computes a five-period forward moving average of X.
convert x=y / transformout=( reverse movave 5 reverse );
In this example, the resulting transformation is
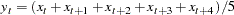 |
Some of the moving time window operators enable you to specify a list of weight values to compute weighted statistics. These are CMOVAVE, CMOVCSS, CMOVGMEAN, CMOVPROD, CMOVSTD, CMOVTVALUE, CMOVUSS, CMOVVAR, MOVAVE, MOVCSS, MOVGMEAN, MOVPROD, MOVSTD, MOVTVALUE, MOVUSS, and MOVVAR.
To specify a weighted moving time window operator, enter the weight values in parentheses after the operator name. The window width  is equal to the number of weights that you specify; do not specify
is equal to the number of weights that you specify; do not specify  .
.
For example, the following statement computes a weighted five-period centered moving average of X.
convert x=y / transformout=( cmovave( .1 .2 .4 .2 .1 ) );
In this example, the resulting transformation is
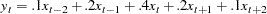 |
The weight values must be greater than zero. If the weights do not sum to 1, the weights specified are divided by their sum to produce the weights used to compute the statistic.
A complete time window is not available at the beginning of the series. For the centered operators a complete window is also not available at the end of the series. The computation of the moving time window operators is adjusted for these boundary conditions as follows.
For backward moving window operators, the width of the time window is shortened at the beginning of the series. For example, the results of the MOVSUM 3 operator are
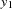 |
 |
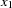 |
|||
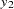 |
 |
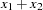 |
|||
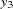 |
 |
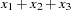 |
|||
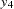 |
 |
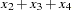 |
|||
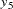 |
 |
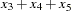 |
|||
 |
 |
 |
For centered moving window operators, the width of the time window is shortened at the beginning and the end of the series due to unavailable observations. For example, the results of the CMOVSUM 5 operator are
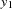 |
 |
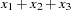 |
|||
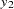 |
 |
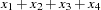 |
|||
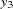 |
 |
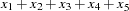 |
|||
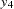 |
 |
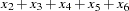 |
|||
 |
 |
 |
|||
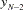 |
 |
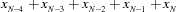 |
|||
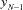 |
 |
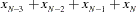 |
|||
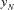 |
 |
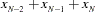 |
For weighted moving time window operators, the weights for the unavailable or unused observations are ignored and the remaining weights renormalized to sum to 1.
Cumulative Statistics Operators
Some operators compute cumulative statistics for a set of current and previous values of the series. The cumulative statistics operators are CUAVE, CUCSS, CUMAX, CUMED, CUMIN, CURANGE, CUSTD, CUSUM, CUUSS, and CUVAR.
By default, the cumulative statistics operators compute the statistics from all previous values of the series, so that 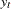 is based on the set of values
is based on the set of values 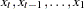 . For example, the following statement computes
. For example, the following statement computes 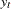 as the cumulative sum of nonmissing
as the cumulative sum of nonmissing 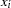 values for
values for 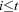 .
.
convert x=y / transformout=( cusum );
You can specify a lag increment argument  for the cumulative statistics operators. In this case, the statistic is computed from the current and every
for the cumulative statistics operators. In this case, the statistic is computed from the current and every 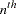 previous value. When
previous value. When  is specified these operators compute statistics of the values
is specified these operators compute statistics of the values 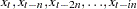 for
for 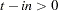 .
.
For example, the following statement computes 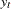 as the cumulative sum of nonmissing
as the cumulative sum of nonmissing 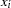 values for odd
values for odd  when
when  is odd and for even
is odd and for even  when
when  is even.
is even.
convert x=y / transformout=( cusum 2 );
The results of this example are
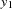 |
 |
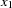 |
|||
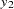 |
 |
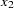 |
|||
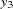 |
 |
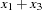 |
|||
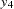 |
 |
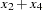 |
|||
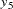 |
 |
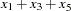 |
|||
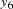 |
 |
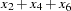 |
|||
 |
 |
 |
Missing Values
You can truncate the length of the result series by using the TRIM, TRIMLEFT, and TRIMRIGHT operators to set values to missing at the beginning or end of the series.
You can use these functions to trim the results of moving time window operators so that the result series contains only values computed from a full width time window. For example, the following statements compute a centered five-period moving average of X, and they set to missing values at the ends of the series that are averages of fewer than five values.
convert x=y / transformout=( cmovave 5 trim 2 );
Normally, the moving time window and cumulative statistics operators ignore missing values and compute their results for the nonmissing values. When preceded by the NOMISS operator, these functions produce a missing result if any value within the time window is missing.
The NOMISS operator does not perform any calculations, but serves to modify the operation of the moving time window operator that follows it. The NOMISS operator has no effect unless it is followed by a moving time window operator.
For example, the following statement computes a five-period moving average of the variable X but produces a missing value when any of the five values are missing.
convert x=y / transformout=( nomiss movave 5 );
The following statement computes the cumulative sum of the variable X but produces a missing value for all periods after the first missing X value.
convert x=y / transformout=( nomiss cusum );
Similar to the NOMISS operator, the MISSONLY operator does not perform any calculations (unless followed by the MEAN option), but it serves to modify the operation of the moving time window operator that follows it. When preceded by the MISSONLY operator, these moving time window operators replace any missing values with the moving statistic and leave nonmissing values unchanged.
For example, the following statement replaces any missing values of the variable X with an exponentially weighted moving average of the past values of X and leaves nonmissing values unchanged. The missing values are interpolated using the specified exponentially weighted moving average. (This is also called simple exponential smoothing.)
convert x=y / transformout=( missonly ewma 0.3 );
The following statement replaces any missing values of the variable X with the overall mean of X.
convert x=y / transformout=( missonly mean );
You can use the SETMISS operator to replace missing values with a specified number. For example, the following statement replaces any missing values of the variable X with the number 8.77.
convert x=y / transformout=( setmiss 8.77 );
Classical Decomposition Operators
If 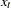 is a seasonal time series with
is a seasonal time series with  observations per season, classical decomposition methods "break down" the time series into four components: trend, cycle, seasonal, and irregular components. The trend and cycle components are often combined to form the trend-cycle component. There are two basic forms of classical decomposition: multiplicative and additive, which are show below.
observations per season, classical decomposition methods "break down" the time series into four components: trend, cycle, seasonal, and irregular components. The trend and cycle components are often combined to form the trend-cycle component. There are two basic forms of classical decomposition: multiplicative and additive, which are show below.
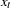 |
 |
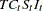 |
|||
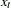 |
 |
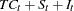 |
where
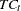
is the trend-cycle component
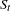
is the seasonal component or seasonal factors that are periodic with period
 and with mean one (multiplicative) or zero (additive)
and with mean one (multiplicative) or zero (additive) 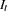
is the irregular or random component that is assumed to have mean one (multiplicative) or zero (additive)
For multiplicative decomposition, all of the 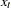 values should be positive.
values should be positive.
The CD_TC operator computes the trend-cycle component for both the multiplicative and additive models. When  is odd, this operator computes an
is odd, this operator computes an  -period centered moving average as follows:
-period centered moving average as follows:
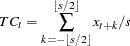 |
For example, in the case where s=5, the CD_TC s operator
convert x=tc / transformout=( cd_tc 5 );
is equivalent to the following CMOVAVE operator:
convert x=tc / transformout=( cmovave 5 trim 2 );
When  is even, the CD_TC s operator computes the average of two adjacent
is even, the CD_TC s operator computes the average of two adjacent  -period centered moving averages as follows:
-period centered moving averages as follows:
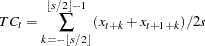 |
For example, in the case where s=12, the CD_TC s operator
convert x=tc / transformout=( cd_tc 12 );
is equivalent to the following CMOVAVE operator:
convert x=tc / transformout=(cmovave 12 movave 2 trim 6);
The CD_S and CDA_S operators compute the seasonal components for the multiplicative and additive models, respectively. First, the trend-cycle component is computed as shown previously. Second, the seasonal-irregular component is computed by 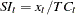 for the multiplicative model and by
for the multiplicative model and by 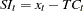 for the additive model. The seasonal component is obtained by averaging the seasonal-irregular component for each season.
for the additive model. The seasonal component is obtained by averaging the seasonal-irregular component for each season.
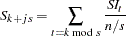 |
where 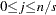 and
and 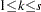 . The seasonal components are normalized to sum to one (multiplicative) or zero (additive).
. The seasonal components are normalized to sum to one (multiplicative) or zero (additive).
The CD_I and CDA_I operators compute the irregular component for the multiplicative and additive models respectively. First, the seasonal component is computed as shown previously. Next, the irregular component is determined from the seasonal-irregular and seasonal components as appropriate.
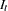 |
 |
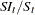 |
|||
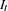 |
 |
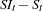 |
The CD_SA and CDA_SA operators compute the seasonally adjusted time series for the multiplicative and additive models, respectively. After decomposition, the original time series can be seasonally adjusted as appropriate.
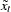 |
 |
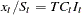 |
|||
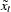 |
 |
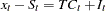 |
The following statements compute all the multiplicative classical decomposition components for the variable X for  =12.
=12.
convert x=tc / transformout=( cd_tc 12 ); convert x=s / transformout=( cd_s 12 ); convert x=i / transformout=( cd_i 12 ); convert x=sa / transformout=( cd_sa 12 );
The following statements compute all the additive classical decomposition components for the variable X for  =4.
=4.
convert x=tc / transformout=( cd_tc 4 ); convert x=s / transformout=( cda_s 4 ); convert x=i / transformout=( cda_i 4 ); convert x=sa / transformout=( cda_sa 4 );
The X12 and X11 procedures provides other methods for seasonal decomposition. See Chapter 32, The X12 Procedure, and Chapter 31, The X11 Procedure.
Fractional Operators
For fractional operators, the parameter, d, represents the order of fractional differencing. Fractional summation is the inverse operation of fractional differencing.
Examples of Usage
Suppose that X is a fractionally integrated time series variable of order d=0.25. Fractionally differencing X forms a time series variable Y which is not integrated.
convert x=y / transformout=(fdif 0.25);
Suppose that Z is a non-integrated time series variable. Fractionally summing Z forms a time series W which is fractionally integrated of order 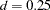 .
.
convert z=w / transformout=(fsum 0.25);
Moving Rank Operators
For the rank operators, the ranks are computed based on the current value with respect to the cumulative, centered, or moving window values. If the current value is missing, the transformed current value is set to missing. If the NOMISS option was previously specified and if any missing values are present in the moving window, the transformed current value is set to missing. Otherwise, redundant values from the moving window are removed and the rank of the current value is computed among the unique values of the moving window.
Examples of Usage
The trades of a particular security are recorded for each weekday in a variable named PRICE. Given the historical daily trades, the ranking of the price of this security for each trading day, considering its entire past history, can be computed as follows:
convert price=history / transformout=( curank );
The ranking of the price of this security for each trading day considering the previous week’s history can be computed as follows:
convert price=lastweek / transformout=( movrank 5 );
The ranking of the price of this security for each trading day considering the previous two week’s history can be computed as follows:
convert price=twoweek / transformout=( movrank 10 );
Moving Product Operators
For the product operators, the current transformed value is computed based on the (weighted) product of the cumulative, centered, or moving window values. If missing values are present in the moving window and the NOMISS operator is previously specified, the current transformed value is set to missing. Otherwise, the current transformed value is set to the (weighted) product of the nonmissing values of the moving window. If the geometric mean is desired, the exponents of each product are normalized to one.
Examples of Usage
The interest rates for a savings account are recorded for each month in the data set variable RATES. The cumulative interest rate for each month considering the entire account past history can be computed as follows:
convert rates=history / transformout=( + 1 cuprod - 1);
The interest rate for each quarter considering the previous quarter’s history can be computed as follows:
convert rates=lastqtr / transformout=( + 1 movprod 3 - 1);
Sequence Operators
For the sequence operators, the sequence values are used to compute the transformed values from the original values in a sequential fashion. You can add to or subtract from the original series or you can multiply or divide by the sequence values. The first sequence value is applied to the first observation of the series, the second sequence value is applied to the second observation of the series, and so on until the end of the sequence is reached. At this point, the first sequence value is applied to the next observation of the series and the second sequence value on the next observation and so on.
Let 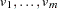 be the sequence values and let
be the sequence values and let 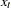 ,
, 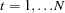 , be the original time series. The transformed series,
, be the original time series. The transformed series, 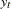 , is computed as follows:
, is computed as follows:
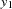 |
 |
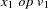 |
|||
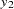 |
 |
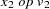 |
|||
 |
 |
 |
|||
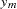 |
 |
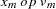 |
|||
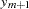 |
 |
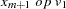 |
|||
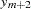 |
 |
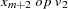 |
|||
 |
 |
 |
|||
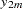 |
 |
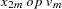 |
|||
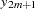 |
 |
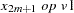 |
|||
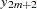 |
 |
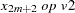 |
|||
 |
 |
 |
where 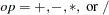 .
.
Examples of Usage
The multiplicative seasonal indices are 0.9, 1.2. 0.8, and 1.1 for the four quarters. Let SEASADJ be a quarterly time series variable that has been seasonally adjusted in a multiplicative fashion. To restore the seasonality to SEASADJ use the following transformation:
convert seasadj=seasonal /
transformout=(seqmult (0.9 1.2 0.8 1.1));
The additive seasonal indices are 4.4, -1.1, -2.1, and -1.2 for the four quarters. Let SEASADJ be a quarterly time series variable that has been seasonally adjusted in additive fashion. To restore the seasonality to SEASADJ use the following transformation:
convert seasadj=seasonal /
transformout=(seqadd (4.4 -1.1 -2.1 -1.2));
Set Operators
For the set operators, the first parameter, 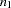 , represents the value to be replaced and the second parameter,
, represents the value to be replaced and the second parameter, 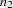 , represents the replacement value. The replacement can be localized to the beginning, middle, or end of the series.
, represents the replacement value. The replacement can be localized to the beginning, middle, or end of the series.
Examples of Usage
Suppose that a store opened recently and that the sales history is stored in a database that does not recognize missing values. Even though demand may have existed prior to the stores opening, this database assigns the value of zero. Modeling the sales history may be problematic because the sales history is mostly zero. To compensate for this deficiency, the leading zero values should be set to missing with the remaining zero values unchanged (representing no demand).
convert sales=demand / transformout=(setleft 0 .);
Likewise, suppose a store is closed recently. The demand may still be present and hence a recorded value of zero does not accurately reflect actual demand.
convert sales=demand / transformout=(setright 0 .);
Scale Operator
For the scale operator, the first parameter, 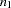 , represents the value associated with the minimum value (
, represents the value associated with the minimum value (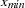 ) and the second parameter,
) and the second parameter, 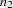 , represents the value associated with the maximum value (
, represents the value associated with the maximum value (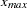 ) of the original series (
) of the original series (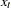 ). The scale operator recales the original data to be between the parameters
). The scale operator recales the original data to be between the parameters 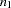 and
and 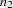 as follows:
as follows:
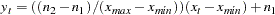 |
Examples of Usage
Suppose that two new product sales histories are stored in variables 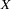 and
and  and you wish to determine their adoption rates. In order to compare their adoption histories the variables must be scaled for comparison.
and you wish to determine their adoption rates. In order to compare their adoption histories the variables must be scaled for comparison.
convert x=w / transformout=(scale 0 1); convert y=z / transformout=(scale 0 1);
Adjust Operator
For the moving summation and product window operators, the window widths at the beginning and end of the series are smaller than those in the middle of the series. Likewise, if there are embedded missing values, the window width is smaller than specified. When preceded by the ADJUST operator, the moving summation (MOVSUM CMOVSUM) and moving product operators (MOVPROD CMOVPROD) are adjusted by the window width.
For example, suppose the variable 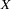 has 10 values and the moving summation operator of width 3 is applied to
has 10 values and the moving summation operator of width 3 is applied to 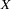 to create the variable
to create the variable  with window width adjustment and the variable
with window width adjustment and the variable  without adjustment.
without adjustment.
convert x=y / transformout=(adjust movsum 3); convert x=z / transformout=(movsum 3);
The above transformations result in the following relationship between  and
and  :
: 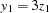 ,
, 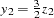 ,
, 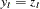 for
for 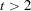 because the first two window widths are smaller than 3.
because the first two window widths are smaller than 3.
For example, suppose the variable 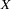 has 10 values and the moving multiplicative operator of width 3 is applied to
has 10 values and the moving multiplicative operator of width 3 is applied to 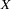 to create the variable
to create the variable  with window width adjustment and the variable
with window width adjustment and the variable  without adjustment.
without adjustment.
convert x=y / transformout=(adjust movprod 3); convert x=z / transformout=(movprod 3);
The above transformation result in the following: 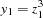 ,
, 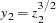 ,
, 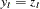 for
for 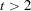 because the first two window widths are smaller than 3.
because the first two window widths are smaller than 3.
Moving T-Value Operators
The moving t-value operators (CUTVALUE, MOVTVALUE, CMOVTVALUE) compute the t-value of the cumulative series or moving window. They can be viewed as combinations of the moving average (CUAVE, MOVAVE, CMOVAVE) and the moving standard deviation (CUSTD, MOVSTD, CMOVSTD), respectively.
Percent Operators
The percentage operators compute the percent summation and the percent difference of the current value and the 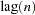 . The percent summation operator (PCTSUM) computes
. The percent summation operator (PCTSUM) computes 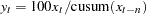 . If any of the values of the preceding equation are missing or the cumulative summation is zero, the result is set to missing. The percent difference operator (PCTDIF) computes
. If any of the values of the preceding equation are missing or the cumulative summation is zero, the result is set to missing. The percent difference operator (PCTDIF) computes 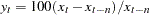 . If any of the values of the preceding equation are missing or the lag value is zero, the result is set to missing.
. If any of the values of the preceding equation are missing or the lag value is zero, the result is set to missing.
For example, suppose variable 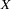 contains the series. The percent summation of lag 4 is applied to
contains the series. The percent summation of lag 4 is applied to 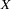 to create the variable
to create the variable  . The percent difference of lag 4 is applied to
. The percent difference of lag 4 is applied to 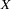 to create the variable
to create the variable  .
.
convert x=y / transformout=(pctsum 4); convert x=z / transformout=(pctdif 4);
Ratio Operators
The ratio operator computes the ratio of the current value and the 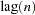 value. The ratio operator (RATIO) computes
value. The ratio operator (RATIO) computes 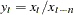 . If any of the values of the preceding equation are missing or the lag value is zero, the result is set to missing.
. If any of the values of the preceding equation are missing or the lag value is zero, the result is set to missing.
For example, suppose variable 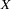 contains the series. The ratio of the current value and the lag 4 value of
contains the series. The ratio of the current value and the lag 4 value of 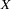 assigned to the variable
assigned to the variable  . The percent ratio of the current value and lag 4 value of
. The percent ratio of the current value and lag 4 value of 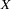 is assigned to the variable
is assigned to the variable  .
.
convert x=y / transformout=(ratio 4); convert x=z / transformout=(ratio 4 * 100);
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
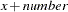
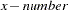
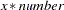
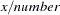
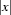
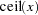
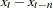
 with
with 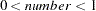 :
: 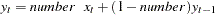 .
. 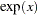
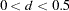
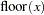
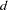
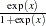
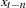
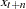
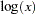
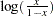
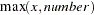
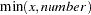
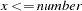 , else x
, else x 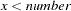 , else x
, else x 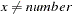 , else x
, else x  = number
= number 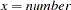 , else x
, else x 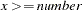 , else x
, else x 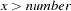 , else x
, else x 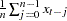
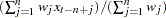

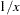
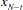
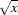
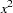
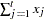
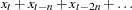
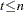 or
or