The STDRATE Procedure

Indirect Standardization and Standardized Morbidity/Mortality Ratio

Subsections:

Indirect standardization compares the rates of the study and reference populations by applying the stratum-specific rates in the reference population to the study population, where the stratum-specific rates might not be reliable.

The expected number of events in the study population is

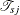\[ {\mathcal E} = \sum _{j} \; {\mathcal T}_{sj} \; {\hat\lambda }_{rj} \]

where ${\mathcal T}_{sj}$ is the population-time in the jth stratum of the study population and 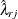${\hat\lambda }_{rj}$ is the rate in the jth stratum of the reference population.

With the expected number of events, 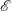${\mathcal E}$, the standardized morbidity ratio or standardized mortality ratio can be expressed as

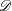\[ {\mathcal R}_{sm} = \; \frac{\, {\mathcal D} \, }{\mathcal E} \]

where ${\mathcal D}$ is the observed number of events (Breslow and Day 1987, p. 65).

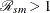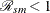The ratio ${\mathcal R}_{sm} > 1$ indicates that the mortality rate or risk in the study population is larger than the estimate in the reference population, and ${\mathcal R}_{sm} < 1$ indicates that the mortality rate or risk in the study population is smaller than the estimate in the reference population.

With the ratio 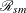${\mathcal R}_{sm}$, an indirectly standardized rate for the study population is computed as

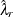\[ {\hat\lambda }_{is} = {\mathcal R}_{sm} \; {\hat\lambda }_ r \]

where ${\hat\lambda }_ r$ is the overall crude rate in the reference population.

Similarly, to compare the risks of the study and reference populations, the stratum-specific risks in the reference population are used to compute the expected number of events in the study population

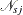\[ {\mathcal E} = \sum _{j} \; {\mathcal N}_{sj} \; {\hat\gamma }_{rj} \]

where ${\mathcal N}_{sj}$ is the number of observations in the jth stratum of the study population and 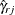${\hat\gamma }_{rj}$ is the risk in the jth stratum of the reference population.

Also, with the standardized morbidity ratio 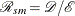${\mathcal R}_{sm} = {\mathcal D} / {\mathcal E}$, an indirectly standardized risk for the study population is computed as

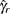\[ {\hat\gamma }_{is} = {\mathcal R}_{sm} \; {\hat\gamma }_ r \]

where ${\hat\gamma }_ r$ is the overall crude risk in the reference population.

The observed number of events in the study population is 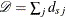${\mathcal D} = \sum _{j} d_{sj}$, where 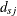$d_{sj}$ is the number of events in the jth stratum of the population. For the rate estimate, if 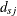$d_{sj}$ has a Poisson distribution, then the variance of the standardized mortality ratio 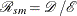${\mathcal R}_{sm} = {\mathcal D} \, / {\mathcal E}$ is

\[ V({\mathcal R}_{sm}) = \frac{\, \, 1}{{\mathcal E}^{2}} \; \sum _{j} \, V(d_{sj}) = \frac{\, 1 \, }{{\mathcal E}^{2}} \; \sum _{j} \, d_{sj} = \frac{\, {\mathcal D} \, }{{\mathcal E}^{2}} = \frac{ {\mathcal R}_{sm} }{\mathcal E} \]

For the risk estimate, if 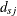$d_{sj}$ has a binomial distribution, then the variance of 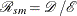${\mathcal R}_{sm} = {\mathcal D} \, / {\mathcal E}$ is

\[ V({\mathcal R}_{sm}) = V \left( \frac{1}{\mathcal E} \; \sum _{j} d_{sj} \right) = \frac{\, \, 1}{{\mathcal E}^{2}} \; \sum _{j} \, V(d_{sj}) = \frac{\, \, 1}{{\mathcal E}^{2}} \; \sum _{j} \, {\mathcal N}_{sj}^{2} V({\hat\gamma }_{sj}) \]

where

\[ V({\hat\gamma }_{sj}) = \frac{ {\hat\gamma }_{sj} (1-{\hat\gamma }_{sj}) }{{\mathcal N}_{sj}} \]

By using the method of statistical differentials (Elandt-Johnson and Johnson 1980, pp. 70–71), the variance of the logarithm of 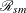${\mathcal R}_{sm}$ can be estimated by

\[ V( \mbox{log}( {\mathcal R}_{sm} ) ) = \frac{1}{ {\mathcal R}_{sm}^{2} } \, V({\mathcal R}_{sm}) \]

For the rate estimate,

\[ V( \mbox{log}( {\mathcal R}_{sm} ) ) = \frac{1}{ {\mathcal R}_{sm}^{2} } \, V({\mathcal R}_{sm}) = \frac{1}{ {\mathcal R}_{sm}^{2} } \, \frac{ {\mathcal R}_{sm} }{\mathcal E} = \frac{1}{ {\mathcal R}_{sm} } \, \frac{1}{\mathcal E} = \frac{1}{\mathcal D} \]

The confidence intervals for 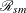${\mathcal R}_{sm}$ can be constructed based on normal, lognormal, and Poisson distributions.

Normal Distribution Confidence Interval for SMR

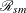A $(1-\alpha )$ confidence interval for ${\mathcal R}_{sm}$ based on a normal distribution is given by

\[ ({\mathcal R}_ l, \; {\mathcal R}_ u)= \left( \; {\mathcal R}_{sm} - z \, \sqrt {V( {\mathcal R}_{sm} )} \, , \; \; {\mathcal R}_{sm} + z \, \sqrt {V( {\mathcal R}_{sm} )} \; \right) \]

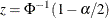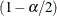where $z = \Phi ^{-1} (1-\alpha /2)$ is the $(1-\alpha /2)$ quantile of the standard normal distribution.

A test statistic for the null hypothesis 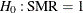$H_0: \mbox{SMR} = 1$ is then given by

\[ \frac{{\mathcal R}_{sm}-1}{ \sqrt {V({\mathcal R}_{sm}}) } \]

The test statistic has an approximate standard normal distribution under 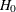$H_0$.

Lognormal Distribution Confidence Interval for SMR

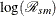A $(1-\alpha )$ confidence interval for $\mbox{log}( {\mathcal R}_{sm})$ based on a normal distribution is given by

\[ \left( \; \mbox{log}({\mathcal R}_{sm}) - z \, \sqrt {V( \mbox{log}({\mathcal R}_{sm}) )} \, , \; \; \mbox{log}({\mathcal R}_{sm}) + z \, \sqrt {V( \mbox{log}({\mathcal R}_{sm}) )} \; \right) \]

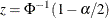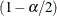where $z = \Phi ^{-1} (1-\alpha /2)$ is the $(1-\alpha /2)$ quantile of the standard normal distribution.

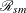Thus, a $(1-\alpha )$ confidence interval for ${\mathcal R}_{sm}$ based on a lognormal distribution is given by

\[ \left( \; {\mathcal R}_{sm} \; e^{ -z {\sqrt { V( \mbox{log}({\mathcal R}_{sm}) ) }}} \, , \; \; {\mathcal R}_{sm} \; e^{ z {\sqrt { V( \mbox{log}({\mathcal R}_{sm}) ) }}} \; \right) \]

A test statistic for the null hypothesis 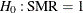$H_0: \mbox{SMR} = 1$ is then given by

\[ \frac{ \mbox{log}({\mathcal R}_{sm})}{ \sqrt {V( \mbox{log}({\mathcal R}_{sm}})) } \]

The test statistic has an approximate standard normal distribution under 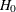$H_0$.

Poisson Distribution Confidence Interval for SMR

Denote the 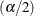$(\alpha /2)$ quantile for the 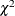$\chi ^{2}$ distribution with 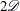$2{\mathcal D}$ degrees of freedom by

\[ q_ l = {( {\chi }_{2 {\mathcal D}}^{2} )}^{-1} \, (\alpha /2) \]

Denote the 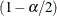$(1-\alpha /2)$ quantiles for the 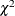$\chi ^{2}$ distribution with 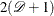$2({\mathcal D}+1)$ degrees of freedom by

\[ q_ u = {( {\chi }_{2 ({\mathcal D}+1)}^{2} )}^{-1}\, (1-\alpha /2) \]

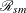Then a $(1-\alpha )$ confidence interval for ${\mathcal R}_{sm}$ based on the 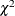$\chi ^{2}$ distribution is given by

\[ ({\mathcal R}_ l, \; {\mathcal R}_ u) = \left( \; \frac{q_ l}{2 \, {\mathcal E}} \, , \; \; \frac{q_ u}{2 \, {\mathcal E}} \right) \]

A p-value for the test of the null hypothesis 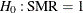$H_0: \mbox{SMR} = 1$ is given by

\[ 2 \, \mr{min} \left( \, \sum _{k=0}^{\mathcal D} \, \frac{ e^{-{\mathcal E}} {\mathcal E}^{k} }{ k! }, \; \sum _{k=\mathcal D}^{\infty } \, \frac{ e^{-{\mathcal E}} {\mathcal E}^{k} }{ k! } \, \right) \]

Indirectly Standardized Rate and Its Confidence Interval

With a rate-standardized mortality ratio 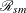${\mathcal R}_{sm}$, an indirectly standardized rate for the study population is computed as

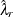\[ {\hat\lambda }_{is} = {\mathcal R}_{sm} \; {\hat\lambda }_ r \]

where ${\hat\lambda }_ r$ is the overall crude rate in the reference population.

The 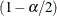$(1-\alpha /2)$ confidence intervals for 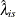${\hat\lambda }_{is}$ can be constructed as

\[ ( {\mathcal R}_ l \, {\hat\lambda }_ r, \; {\mathcal R}_ u \, {\hat\lambda }_ r ) \]

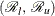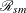where $({\mathcal R}_ l, \; {\mathcal R}_ u)$ is the confidence interval for ${\mathcal R}_{sm}$.

Indirectly Standardized Risk and Its Confidence Interval

With a risk-standardized mortality ratio 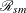${\mathcal R}_{sm}$, an indirectly standardized risk for the study population is computed as

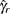\[ {\hat\gamma }_{is} = {\mathcal R}_{sm} \; {\hat\gamma }_ r \]

where ${\hat\gamma }_ r$ is the overall crude risk in the reference population.

The 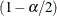$(1-\alpha /2)$ confidence intervals for 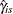${\hat\gamma }_{is}$ can be constructed as

\[ ( {\mathcal R}_ l \, {\hat\gamma }_ r, \; {\mathcal R}_ u \, {\hat\gamma }_ r ) \]

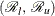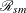where $({\mathcal R}_ l, \; {\mathcal R}_ u)$ is the confidence interval for ${\mathcal R}_{sm}$.