The STDRATE Procedure

Rate

Subsections:

A major task in epidemiology is to compare event frequencies for groups of people. Both rate and risk are commonly used to measure event frequency in the comparison. Rate is a measure of change in one quantity per unit of another quantity. An event rate measures how fast the events are occurring. In contrast, an event risk is the probability that an event occurs over a specified follow-up time period.

An event rate of a population over a specified time period can be defined as the number of new events divided by the population-time of the population over the same time period,

\[ {\hat\lambda } = \frac{d}{\mathcal T} \]

where d is the number of events and ${\mathcal T}$ is the population-time that is computed by adding up the time contributed by each subject in the population over the specified time period.

For a general population, the subsets (strata) might not be homogeneous enough to have a similar rate. Thus, the rate for each stratum should be computed separately to reflect this discrepancy. For a population that consists of K homogeneous strata (such as different age groups), the stratum-specific rate for the jth stratum in a population is computed as

\[ {\hat\lambda }_ j = \frac{d_{j}}{{\mathcal T}_{j}} \]

where $d_{j}$ is the number of events and ${\mathcal T}_{j}$ is the population-time for subjects in the jth stratum of the population.

Assuming the number of events in the jth stratum, $d_{j}$, has a Poisson distribution, the variance of ${\hat\lambda }_ j$ is

\[ V( {\hat\lambda }_ j ) = V( \frac{d_{j}}{{\mathcal T}_{j}} ) = \, \frac{1}{{\mathcal T_{j}}^{2}} \, V( d_{j} ) = \, \frac{d_{j}}{{\mathcal T}_{j}^{2}} = \, \frac{\hat\lambda _{j}}{{\mathcal T}_{j}} \]

By using the method of statistical differentials (Elandt-Johnson and Johnson 1980, pp. 70–71), the variance of the logarithm of rate can be estimated by

\[ V( \mbox{log}( {\hat\lambda }_ j ) ) = \frac{1}{ {\hat\lambda }_{j}^{2} } \, V( {\hat\lambda }_{j} ) = \frac{1}{ {\hat\lambda }_{j}^{2} } \, \frac{\hat\lambda _{j}}{{\mathcal T}_{j}} = \frac{1}{ {\hat\lambda }_{j} \, {\mathcal T}_{j} } = \frac{1}{ d_{j} } \]

Because the rate value can be very small, especially for rare events, it is sometimes expressed in terms of the product of a multiplier and the rate itself. For example, a rate can be expressed as the number of events per 100,000 person-years.

Normal Distribution Confidence Interval for Rate

A 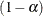$(1-\alpha )$ confidence interval for ${\hat\lambda }_{j}$ based on a normal distribution is given by

\[ \left( \; {\hat\lambda }_{j} - z \, \sqrt {V( {\hat\lambda }_{j} )} \, , \; \; {\hat\lambda }_{j} + z \, \sqrt {V( {\hat\lambda }_{j} )} \; \right) \]

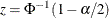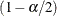where $z = \Phi ^{-1} (1-\alpha /2)$ is the $(1-\alpha /2)$ quantile of the standard normal distribution.

Lognormal Distribution Confidence Interval for Rate

A 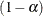$(1-\alpha )$ confidence interval for $\mbox{log}( {\hat\lambda }_{j} )$ based on a normal distribution is given by

\[ \left( \; \mbox{log}({\hat\lambda }_{j}) - z \, \sqrt {V( \mbox{log}({\hat\lambda }_{j}) )} \, , \; \; \mbox{log}({\hat\lambda }_{j}) + z \, \sqrt {V( \mbox{log}({\hat\lambda }_{j}) )} \; \right) \]

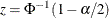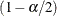where $z = \Phi ^{-1} (1-\alpha /2)$ is the $(1-\alpha /2)$ quantile of the standard normal distribution and the variance $V( \mbox{log}({\hat\lambda }_{j}) ) = 1 / d_{j}$.

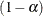Thus, a $(1-\alpha )$ confidence interval for ${\hat\lambda }_{j}$ based on a lognormal distribution is given by

\[ \left( \; {\hat\lambda }_{j} \; e^{ -\frac{z}{\sqrt {d_{j}}} } \, , \; \; {\hat\lambda }_{j} \; e^{ \frac{z}{\sqrt {d_{j}}} } \; \right) \]

Poisson Distribution Confidence Interval for Rate

Denote the 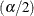$(\alpha /2)$ quantile for the 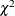$\chi ^{2}$ distribution with $2 \, d_ j$ degrees of freedom by

\[ q_{lj} = {( {\chi }_{2 \, d_ j}^{2} )}^{-1} \, (\alpha /2) \]

Denote the 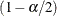$(1-\alpha /2)$ quantiles for the 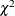$\chi ^{2}$ distribution with $2(d_ j+1)$ degrees of freedom by

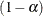\[ q_{uj} = {( {\chi }_{2 \, (d_ j+1)}^{2} )}^{-1}\, (1-\alpha /2) \]

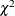Then a $(1-\alpha )$ confidence interval for ${\hat\lambda }_{j}$ based on the $\chi ^{2}$ distribution is given by

\[ \left( \; \frac{q_{lj}}{2 \, {\mathcal T}_{j}} \, , \; \; \frac{q_{uj}}{2 \, {\mathcal T}_{j}} \right) \]

Confidence Interval for Rate Difference Statistic

For rate estimates from two independent samples, ${\hat\lambda }_{1j}$ and ${\hat\lambda }_{2j}$, a $(1-\alpha 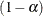)$ confidence interval for the rate difference ${\hat\lambda }_{dj} = {\hat\lambda }_{1j} - {\hat\lambda }_{2j}$ is

\[ \left( \; {\hat\lambda }_{dj} - z \, \sqrt {V( {\hat\lambda }_{dj} )} \, , \; \; {\hat\lambda }_{dj} + z \, \sqrt {V( {\hat\lambda }_{dj} )} \; \right) \]

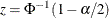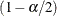where $z = \Phi ^{-1} (1-\alpha /2)$ is the $(1-\alpha /2)$ quantile of the standard normal distribution and the variance

\[ V({\hat\lambda }_{dj}) = V({\hat\lambda }_{1j}) + V({\hat\lambda }_{2j}) \]

Confidence Interval for Rate Ratio Statistic

For rate estimates from two independent samples, ${\hat\lambda }_{1j}$ and ${\hat\lambda }_{2j}$, a $(1-\alpha 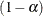)$ confidence interval for the log rate ratio statistic $\mbox{log} ({\hat\lambda }_{rj}) = \mbox{log} ({\hat\lambda }_{1j} / {\hat\lambda }_{2j})$ is

\[ \left( \; \mbox{log} ({\hat\lambda }_{rj}) - z \, \sqrt {V( \mbox{log} ({\hat\lambda }_{rj}) )} \, , \; \; \mbox{log} ({\hat\lambda }_{rj}) + z \, \sqrt {V( \mbox{log} ({\hat\lambda }_{rj}) )} \; \right) \]

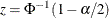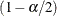where $z = \Phi ^{-1} (1-\alpha /2)$ is the $(1-\alpha /2)$ quantile of the standard normal distribution and the variance

\[ V( \mbox{log} ({\hat\lambda }_{rj}) ) = V( \mbox{log} ({\hat\lambda }_{1j}) ) + V( \mbox{log} ({\hat\lambda }_{2j}) ) \]

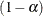Thus, a $(1-\alpha )$ confidence interval for the rate ratio statistic 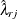${\hat\lambda }_{rj}$ is given by

\[ \left( \; \frac{{\hat\lambda }_{1j}}{{\hat\lambda }_{2j}} \; e^{ -z \sqrt { V( \mbox{log} ({\hat\lambda }_{rj}) ) } } \, , \; \; \frac{{\hat\lambda }_{1j}}{{\hat\lambda }_{2j}} \; e^{ z \sqrt { V( \mbox{log} ({\hat\lambda }_{rj}) ) } } \; \right) \]

Confidence Interval for Rate SMR

At stratum j, a stratum-specific standardized morbidity/mortality ratio is

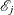\[ {\mathcal R}_{j} = \; \frac{\, d_ j \, }{{\mathcal E}_ j} \]

where ${\mathcal E}_ j$ is the expected number of events.

With the rate

\[ {\hat\lambda }_ j = \frac{d_{j}}{{\mathcal T}_{j}} \]

SMR can be expressed as

\[ {\mathcal R}_ j = \; \frac{\, {\mathcal T}_ j \, }{{\mathcal E}_ j} \; {\hat\lambda }_ j \]

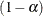Thus, a $(1-\alpha )$ confidence interval for 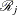${\mathcal R}_ j$ is given by

\[ \left( \; \frac{\, {\mathcal T}_ j \, }{{\mathcal E}_ j} \; {\hat\lambda }_{jl} \, , \; \; \frac{\, {\mathcal T}_ j \, }{{\mathcal E}_ j} \; {\hat\lambda }_{ju} \; \right) \]

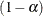where $(\, {\hat\lambda }_{jl} \, , \, {\hat\lambda }_{ju} \, )$ is a $(1-\alpha )$ confidence interval for the rate ${\hat\lambda }_ j$.