The STDIZE Procedure
The following example demonstrates how you can use the STDIZE procedure to obtain location and scale measures of your data.
In the following hypothetical data set, a random sample of grade twelve students is selected from a number of coeducational schools. Each school is classified as one of two types: Urban or Rural. There are 40 observations.
The variables are id (student identification), Type (type of school attended: ‘urban’=urban area and ‘rural’=rural area), and total (total assessment scores in History, Geometry, and Chemistry).
The following DATA step creates the SAS data set TotalScores.
data TotalScores; title 'High School Scores Data'; input id Type $ total @@; datalines; 1 rural 135 2 rural 125 3 rural 223 4 rural 224 5 rural 133 6 rural 253 7 rural 144 8 rural 193 9 rural 152 10 rural 178 11 rural 120 12 rural 180 13 rural 154 14 rural 184 15 rural 187 16 rural 111 17 rural 190 18 rural 128 19 rural 110 20 rural 217 21 urban 192 22 urban 186 23 urban 64 24 urban 159 25 urban 133 26 urban 163 27 urban 130 28 urban 163 29 urban 189 30 urban 144 31 urban 154 32 urban 198 33 urban 150 34 urban 151 35 urban 152 36 urban 151 37 urban 127 38 urban 167 39 urban 170 40 urban 123 ;
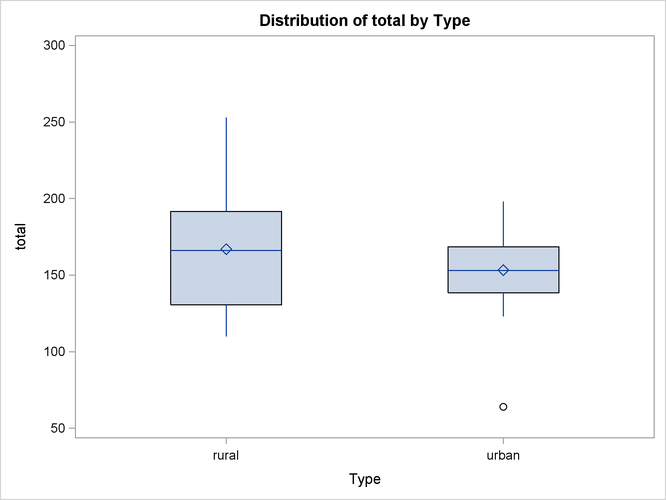
Suppose you now want to standardize the total scores in different types of schools prior to any further analysis. Before standardizing the total scores, you can use the box plot from PROC BOXPLOT to summarize the total scores for both types of schools.
ods graphics on; proc boxplot data=TotalScores; plot total*Type / boxstyle=schematic noserifs; run;
The PLOT statement in the PROC BOXPLOT statement creates the schematic plots (without the serifs) when you specify boxstyle=schematic noserifs. Figure 87.1 displays a box plot for each type of school.
Inspection reveals that one urban score is a low outlier. Also, if you compare the lengths of two box plots, there seems to be twice as much dispersion for the rural scores as for the urban scores.
The following PROC UNIVARIATE statement reports the information about the extreme values of the Score variable for each type of school:
proc univariate data=TotalScores; var total; by Type; run;
Figure 87.2 displays the table from PROC UNIVARIATE for the lowest and highest five total scores for urban schools. The outlier (Obs = 23), marked in Figure 87.2 by the symbol '0', has a score of 64.
Figure 87.2: Table for Extreme Observations When Type=urban
| High School Scores Data |
| Extreme Observations | |||
|---|---|---|---|
| Lowest | Highest | ||
| Value | Obs | Value | Obs |
| 64 | 23 | 170 | 39 |
| 123 | 40 | 186 | 22 |
| 127 | 37 | 189 | 29 |
| 130 | 27 | 192 | 21 |
| 133 | 25 | 198 | 32 |
The following PROC STDIZE procedure requests the METHOD=STD option for computing the location and scale measures:
proc stdize data=totalscores method=std pstat; title2 'METHOD=STD'; var total; by Type; run;
Figure 87.3 displays the table of location and scale measures from the PROC STDIZE statement. PROC STDIZE uses the sample mean as the location measure and the sample standard deviation as the scale measure for standardizing. The PSTAT option displays a table containing these two measures.
Figure 87.3: Location and Scale Measures Table When METHOD=STD
| High School Scores Data |
| METHOD=STD |
| Location and Scale Measures | |||
|---|---|---|---|
| Location = mean Scale = standard deviation | |||
| Name | Location | Scale | N |
| total | 167.050000 | 41.956713 | 20 |
| High School Scores Data |
| METHOD=STD |
| Location and Scale Measures | |||
|---|---|---|---|
| Location = mean Scale = standard deviation | |||
| Name | Location | Scale | N |
| total | 153.300000 | 30.066768 | 20 |
The ratio of the scale of rural scores to the scale of urban scores is approximately 1.4 (41.96/30.07). This ratio is smaller than the dispersion ratio observed in the previous schematic plots.
The STDIZE procedure provides several location and scale measures that are resistant to outliers. The following statements invoke three different standardization methods and display the tables for the location and scale measures:
proc stdize data=totalscores method=mad pstat; title2 'METHOD=MAD'; var total; by Type; run;
proc stdize data=totalscores method=iqr pstat; title2 'METHOD=IQR'; var total; by Type; run;
proc stdize data=totalscores method=abw(4) pstat; title2 'METHOD=ABW(4)'; var total; by Type; run;
Figure 87.4 displays the table of location and scale measures when the standardization method is median absolute deviation (MAD). The location measure is the median, and the scale measure is the median absolute deviation from the median. The ratio of the scale of rural scores to the scale of urban scores is approximately 2.06 (32.0/15.5) and is close to the dispersion ratio observed in the previous schematic plots.
Figure 87.4: Location and Scale Measures Table When METHOD=MAD
| High School Scores Data |
| METHOD=MAD |
| Location and Scale Measures | |||
|---|---|---|---|
| Location = median Scale = median abs dev from median |
|||
| Name | Location | Scale | N |
| total | 166.000000 | 32.000000 | 20 |
| High School Scores Data |
| METHOD=MAD |
| Location and Scale Measures | |||
|---|---|---|---|
| Location = median Scale = median abs dev from median |
|||
| Name | Location | Scale | N |
| total | 153.000000 | 15.500000 | 20 |
Figure 87.5 displays the table of location and scale measures when the standardization method is IQR. The location measure is the median, and the scale measure is the interquartile range. The ratio of the scale of rural scores to the scale of urban scores is approximately 2.03 (61/30) and is, in fact, the dispersion ratio observed in the previous schematic plots.
Figure 87.5: Location and Scale Measures Table When METHOD=IQR
| High School Scores Data |
| METHOD=IQR |
| Location and Scale Measures | |||
|---|---|---|---|
| Location = median Scale = interquartile range |
|||
| Name | Location | Scale | N |
| total | 166.000000 | 61.000000 | 20 |
| High School Scores Data |
| METHOD=IQR |
| Location and Scale Measures | |||
|---|---|---|---|
| Location = median Scale = interquartile range |
|||
| Name | Location | Scale | N |
| total | 153.000000 | 30.000000 | 20 |
Figure 87.6 displays the table of location and scale measures when the standardization method is ABW, for which the location measure is the biweight one-step M-estimate, and the scale measure is the biweight A-estimate. Note that the initial estimate for ABW is MAD. The following steps help to decide the value of the tuning constant:
-
For rural scores, the location estimate for MAD is 166.0, and the scale estimate for MAD is 32.0. The maximum of the rural scores is 253 (not shown), and the minimum is 110 (not shown). Thus, the tuning constant needs to be 3 so that it does not reject any observation that has a score between 110 to 253.
-
For urban scores, the location estimate for MAD is 153.0, and the scale estimate for MAD is 15.5. The maximum of the rural scores is 198, and the minimum (also an outlier) is 64. Thus, the tuning constant needs to be 4 so that it rejects the outlier (64) but includes the maximum (198) as an normal observation.
-
The maximum of the tuning constants, obtained in steps 1 and 2, is 4.
See Goodall (1983, Chapter 11) for details about the tuning constant. The ratio of the scale of rural scores to the scale of urban scores is approximately 2.06 (32.0/15.5). It is also close to the dispersion ratio observed in the previous schematic plots.
Figure 87.6: Location and Scale Measures Table When METHOD=ABW
| High School Scores Data |
| METHOD=ABW(4) |
| Location and Scale Measures | |||
|---|---|---|---|
| Location = biweight 1-step M-estimate Scale = biweight A-estimate |
|||
| Name | Location | Scale | N |
| total | 162.889603 | 56.662855 | 20 |
| High School Scores Data |
| METHOD=ABW(4) |
| Location and Scale Measures | |||
|---|---|---|---|
| Location = biweight 1-step M-estimate Scale = biweight A-estimate |
|||
| Name | Location | Scale | N |
| total | 156.014608 | 28.615980 | 20 |
The preceding analysis shows that METHOD=MAD, METHOD=IQR, and METHOD=ABW all provide better dispersion ratios than METHOD=STD does.
You can recompute the standard deviation after deleting the outlier from the original data set for comparison. The following
statements create a data set NoOutlier that excludes the outlier from the TotalScores data set and invoke PROC STDIZE with METHOD=STD.
data NoOutlier; set totalscores; if (total = 64) then delete; run;
proc stdize data=NoOutlier method=std pstat; title2 'After Removing Outlier, METHOD=STD'; var total; by Type; run;
Figure 87.7 displays the location and scale measures after deleting the outlier. The lack of resistance of the standard deviation to outliers is clearly illustrated: if you delete the outlier, the sample standard deviation of urban scores changes from 30.07 to 22.09. The new ratio of the scale of rural scores to the scale of urban scores is approximately 1.90 (41.96/22.09).
Figure 87.7: Location and Scale Measures Table When METHOD=STD without the Outlier
| High School Scores Data |
| After Removing Outlier, METHOD=STD |
| Location and Scale Measures | |||
|---|---|---|---|
| Location = mean Scale = standard deviation | |||
| Name | Location | Scale | N |
| total | 167.050000 | 41.956713 | 20 |
| High School Scores Data |
| After Removing Outlier, METHOD=STD |
| Location and Scale Measures | |||
|---|---|---|---|
| Location = mean Scale = standard deviation | |||
| Name | Location | Scale | N |
| total | 158.000000 | 22.088207 | 19 |