Example 26.15 Comparing the ML and FIML Estimation
This example uses the complete data set from Example 26.12 to illustrate how the maximum likelihood (ML) and full information maximum likelihood (FIML) methods are theoretically equivalent when you apply them to data set without missing values. In Example 26.14, you apply a confirmatory factor model to a data set with missing values. You find that with METHOD=FIML, you can get more stable estimates than with METHOD=ML (which is the default estimation method). Near the end of Example 26.14, you learn that ML and FIML are theoretically equivalent estimation methods when you apply them to data sets without missing values.
However, the ML and FIML methods have two major computational differences in their implementations in PROC CALIS. First, with METHOD=FIML the first-order properties (that is, the means of the variables) of the data are automatically included in the analysis. However, by default you analyze only the second-order properties (that is, the covariances of the variables) with METHOD=ML. Second, the biased sample covariance formula (with N as the variance divisor) is used with METHOD=FIML, while the unbiased sample covariance formula (with DF=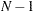 as the variance divisor) is used with METHOD=ML. See the section Relationships among Estimation Criteria for more details about the similarities and differences between the ML and FIML methods.
as the variance divisor) is used with METHOD=ML. See the section Relationships among Estimation Criteria for more details about the similarities and differences between the ML and FIML methods.
If you take care of these two differences between ML and FIML in PROC CALIS, you can obtain exactly the same results with these two methods when you apply them to data sets without missing values.
For example, with the complete data set scores from Example 26.12, you specify the FIML estimation in the following statements:
proc calis method=fiml data=scores;
factor
verbal ---> x1-x3,
math ---> y1-y3;
pvar
verbal = 1.,
math = 1.;
run;
An equivalent specification with the ML method is shown in the following statements:
proc calis method=ml meanstr vardef=n data=scores;
factor
verbal ---> x1-x3,
math ---> y1-y3;
pvar
verbal = 1.,
math = 1.;
run;
In the PROC CALIS statement, you specify two options to make the ML estimation exactly equivalent to the FIML estimation in PROC CALIS. First, the MEANSTR option requests the first-order properties (the mean structures) to be analyzed with the covariance structures. Second, the VARDEF=N option defines the variance divisor to N, instead of the default DF, which is the same as N 1. These two options make the ML estimation equivalent to the FIML estimation.
1. These two options make the ML estimation equivalent to the FIML estimation.
Output 26.15.1 and Output 26.15.2 show some fit summary statistics under the FIML and ML methods, respectively.
Output 26.15.1
Model Fitting by the FIML Method: Scores Data
| 31.7837 |
| 10.1215 |
| 8 |
| 0.2566 |
| 0.0504 |
| 0.0910 |
| 0.9872 |
Output 26.15.2
Model Fitting by the ML Method: Scores Data
| 0.3163 |
| 10.1215 |
| 8 |
| 0.2566 |
| 0.0504 |
| 0.0910 |
| 0.9872 |
Except for the fit function values, both FIML and ML methods produce the same set of fit statistics. The difference in the fit function values is expected because the FIML function has a constant term which is derived from the likelihood function. This constant term does not depend on the model parameters. Hence, the FIML and ML discrepancy functions that are used in PROC CALIS are equivalent when VARDEF=N is used in the ML method for analyzing mean and covariance structures.
The parameter estimates are shown in Output 26.15.3 and Output 26.15.4 for the FIML and ML methods, respectively. Except for very tiny numerical differences in some estimates, the FIML and ML estimates match.
Output 26.15.3
Parameter Estimates by the FIML Method: Scores Data
| 5.7486 |
| 0.9651 |
| 5.9567 |
| [_Parm1] |
|
|
| 5.7265 |
| 0.9239 |
| 6.1980 |
| [_Parm2] |
|
|
| 4.5886 |
| 0.7570 |
| 6.0618 |
| [_Parm3] |
|
|
|
| 5.1972 |
| 0.6779 |
| 7.6662 |
| [_Parm4] |
|
|
| 4.1342 |
| 0.6025 |
| 6.8612 |
| [_Parm5] |
|
|
| 3.7004 |
| 0.6143 |
| 6.0237 |
| [_Parm6] |
|
|
| 0.5175 |
| 0.1406 |
| 3.6804 |
| [_Add01] |
|
| 0.5175 |
| 0.1406 |
| 3.6804 |
| [_Add01] |
|
|
| _Add02 |
19.90625 |
1.17540 |
16.93575 |
| _Add03 |
18.81250 |
1.14089 |
16.48928 |
| _Add04 |
18.68750 |
0.92749 |
20.14856 |
| _Add05 |
17.90625 |
0.93161 |
19.22084 |
| _Add06 |
17.84375 |
0.78823 |
22.63773 |
| _Add07 |
17.75000 |
0.76419 |
23.22725 |
| _Add08 |
11.16406 |
4.06574 |
2.74589 |
| _Add09 |
8.85978 |
3.65403 |
2.42466 |
| _Add10 |
6.47248 |
2.47685 |
2.61319 |
| _Add11 |
0.76135 |
1.23420 |
0.61687 |
| _Add12 |
2.79060 |
1.04306 |
2.67539 |
| _Add13 |
4.99466 |
1.40025 |
3.56698 |
Output 26.15.4
Parameter Estimates by the ML Method: Scores Data
| 5.7486 |
| 0.9651 |
| 5.9567 |
| [_Parm1] |
|
|
| 5.7265 |
| 0.9239 |
| 6.1981 |
| [_Parm2] |
|
|
| 4.5885 |
| 0.7570 |
| 6.0617 |
| [_Parm3] |
|
|
|
| 5.1972 |
| 0.6779 |
| 7.6662 |
| [_Parm4] |
|
|
| 4.1341 |
| 0.6025 |
| 6.8612 |
| [_Parm5] |
|
|
| 3.7004 |
| 0.6143 |
| 6.0238 |
| [_Parm6] |
|
|
| 0.5175 |
| 0.1406 |
| 3.6800 |
| [_Add01] |
|
| 0.5175 |
| 0.1406 |
| 3.6800 |
| [_Add01] |
|
|
| _Add02 |
19.90625 |
1.17540 |
16.93575 |
| _Add03 |
18.81250 |
1.14089 |
16.48928 |
| _Add04 |
18.68750 |
0.92749 |
20.14856 |
| _Add05 |
17.90625 |
0.93161 |
19.22084 |
| _Add06 |
17.84375 |
0.78823 |
22.63773 |
| _Add07 |
17.75000 |
0.76419 |
23.22725 |
| _Add08 |
11.16365 |
4.06567 |
2.74583 |
| _Add09 |
8.85925 |
3.65397 |
2.42456 |
| _Add10 |
6.47288 |
2.47689 |
2.61331 |
| _Add11 |
0.76124 |
1.23420 |
0.61679 |
| _Add12 |
2.79066 |
1.04307 |
2.67543 |
| _Add13 |
4.99461 |
1.40024 |
3.56697 |
The equivalence between METHOD=ML and METHOD=FIML implies that if you do not have any missing data in your data, you can just use METHOD=ML because it is computationally more efficient than the FIML method.
While the equivalence between ML and FIML is established here with the use of the VARDEF= and MEANSTR options (for data without missing values), it is not necessary in practice to use these options with METHOD=ML. The VARDEF= option is used in this example only to demonstrate the theoretical equivalence between METHOD=ML and METHOD=FIML. The VARDEF= option has very little effect if you have at least a moderate sample size (for example, 30 or more observations).
Merely adding the MEANSTR option to an analysis for data without missing values amounts to adding a saturated mean structure to a covariance structure analysis. In this case, the MEANSTR option only gives you more estimates that pertain to the mean structures, but the parameter estimates that pertain to the covariance structures do not change. Therefore, use the MEANSTR option only when you need to estimate certain mean structure parameters or when you fit models with nonsaturated mean structures.
However, use METHOD=FIML when there are missing values in your data and you need to use every bit of information from the incomplete observations with random missing values.


 Classes of Statements in PROC CALIS Single-Group Analysis Syntax Multiple-Group Multiple-Model Analysis Syntax PROC CALIS Statement BOUNDS Statement BY Statement COSAN Statement COV Statement DETERM Statement EFFPART Statement FACTOR Statement FITINDEX Statement FREQ Statement GROUP Statement LINCON Statement LINEQS Statement LISMOD Statement LMTESTS Statement MATRIX Statement MEAN Statement MODEL Statement MSTRUCT Statement NLINCON Statement NLOPTIONS Statement OUTFILES Statement PARAMETERS Statement PARTIAL Statement PATH Statement PCOV Statement PVAR Statement RAM Statement REFMODEL Statement RENAMEPARM Statement SAS Programming Statements SIMTESTS Statement STD Statement STRUCTEQ Statement TESTFUNC Statement VAR Statement VARIANCE Statement VARNAMES Statement WEIGHT Statement
Classes of Statements in PROC CALIS Single-Group Analysis Syntax Multiple-Group Multiple-Model Analysis Syntax PROC CALIS Statement BOUNDS Statement BY Statement COSAN Statement COV Statement DETERM Statement EFFPART Statement FACTOR Statement FITINDEX Statement FREQ Statement GROUP Statement LINCON Statement LINEQS Statement LISMOD Statement LMTESTS Statement MATRIX Statement MEAN Statement MODEL Statement MSTRUCT Statement NLINCON Statement NLOPTIONS Statement OUTFILES Statement PARAMETERS Statement PARTIAL Statement PATH Statement PCOV Statement PVAR Statement RAM Statement REFMODEL Statement RENAMEPARM Statement SAS Programming Statements SIMTESTS Statement STD Statement STRUCTEQ Statement TESTFUNC Statement VAR Statement VARIANCE Statement VARNAMES Statement WEIGHT Statement Input Data Sets Output Data Sets The COSAN Model The FACTOR Model The LINEQS Model The LISMOD Model and Submodels The MSTRUCT Model The PATH Model The RAM Model Naming Variables and Parameters Setting Constraints on Parameters Automatic Variable Selection Estimation Criteria Relationships among Estimation Criteria Gradient, Hessian, Information Matrix, and Approximate Standard Errors Counting the Degrees of Freedom Assessment of Fit Total, Direct, and Indirect Effects Standardized Solutions Modification Indices Missing Values and the Analysis of Missing Patterns Measures of Multivariate Kurtosis Initial Estimates Use of Optimization Techniques Computational Problems Displayed Output ODS Table Names ODS Graphics
Input Data Sets Output Data Sets The COSAN Model The FACTOR Model The LINEQS Model The LISMOD Model and Submodels The MSTRUCT Model The PATH Model The RAM Model Naming Variables and Parameters Setting Constraints on Parameters Automatic Variable Selection Estimation Criteria Relationships among Estimation Criteria Gradient, Hessian, Information Matrix, and Approximate Standard Errors Counting the Degrees of Freedom Assessment of Fit Total, Direct, and Indirect Effects Standardized Solutions Modification Indices Missing Values and the Analysis of Missing Patterns Measures of Multivariate Kurtosis Initial Estimates Use of Optimization Techniques Computational Problems Displayed Output ODS Table Names ODS Graphics Estimating Covariances and Correlations Estimating Covariances and Means Simultaneously Testing Uncorrelatedness of Variables Testing Covariance Patterns Testing Some Standard Covariance Pattern Hypotheses Linear Regression Model Multivariate Regression Models Measurement Error Models Testing Specific Measurement Error Models Measurement Error Models with Multiple Predictors Measurement Error Models Specified As Linear Equations Confirmatory Factor Models Confirmatory Factor Models: Some Variations The Full Information Maximum Likelihood Method Comparing the ML and FIML Estimation Path Analysis: Stability of Alienation Simultaneous Equations with Mean Structures and Reciprocal Paths Fitting Direct Covariance Structures Confirmatory Factor Analysis: Cognitive Abilities Testing Equality of Two Covariance Matrices Using a Multiple-Group Analysis Testing Equality of Covariance and Mean Matrices between Independent Groups Illustrating Various General Modeling Languages Testing Competing Path Models for the Career Aspiration Data Fitting a Latent Growth Curve Model Higher-Order and Hierarchical Factor Models Linear Relations among Factor Loadings Multiple-Group Model for Purchasing Behavior Fitting the RAM and EQS Models by the COSAN Modeling Language Second-Order Confirmatory Factor Analysis Linear Relations among Factor Loadings: COSAN Model Specification Ordinal Relations among Factor Loadings Longitudinal Factor Analysis
Estimating Covariances and Correlations Estimating Covariances and Means Simultaneously Testing Uncorrelatedness of Variables Testing Covariance Patterns Testing Some Standard Covariance Pattern Hypotheses Linear Regression Model Multivariate Regression Models Measurement Error Models Testing Specific Measurement Error Models Measurement Error Models with Multiple Predictors Measurement Error Models Specified As Linear Equations Confirmatory Factor Models Confirmatory Factor Models: Some Variations The Full Information Maximum Likelihood Method Comparing the ML and FIML Estimation Path Analysis: Stability of Alienation Simultaneous Equations with Mean Structures and Reciprocal Paths Fitting Direct Covariance Structures Confirmatory Factor Analysis: Cognitive Abilities Testing Equality of Two Covariance Matrices Using a Multiple-Group Analysis Testing Equality of Covariance and Mean Matrices between Independent Groups Illustrating Various General Modeling Languages Testing Competing Path Models for the Career Aspiration Data Fitting a Latent Growth Curve Model Higher-Order and Hierarchical Factor Models Linear Relations among Factor Loadings Multiple-Group Model for Purchasing Behavior Fitting the RAM and EQS Models by the COSAN Modeling Language Second-Order Confirmatory Factor Analysis Linear Relations among Factor Loadings: COSAN Model Specification Ordinal Relations among Factor Loadings Longitudinal Factor Analysis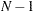 as the variance divisor) is used with METHOD=ML. See the section Relationships among Estimation Criteria for more details about the similarities and differences between the ML and FIML methods.
as the variance divisor) is used with METHOD=ML. See the section Relationships among Estimation Criteria for more details about the similarities and differences between the ML and FIML methods.  1. These two options make the ML estimation equivalent to the FIML estimation.
1. These two options make the ML estimation equivalent to the FIML estimation.