The NLP Procedure

NLINCON Statement

NLINCON nlcon [ , nlcon ...] [ / option ] ;

NLC nlcon [ , nlcon ...] [ / option ] ;

where nlcon is given in one of the following formats:

number operator variable_list operator number
number operator variable_list
variable_list operator number

and operator is $\leq , <, \geq , >,$ or $=$ . The value of option can be SUMOBS or EVERYOBS.

General nonlinear equality and inequality constraints are specified with the NLINCON statement. The syntax of the NLINCON statement is similar to that of the BOUNDS statement with two small additions:

The BOUNDS statement can contain only the names of decision variables. The NLINCON statement can also contain the names of continuous functions of the decision variables. These functions must be computed in the program statements, and since they can depend on the values of some of the variables in the DATA= data set, there are two possibilities:
- If the continuous functions should be summed across all observations read from the DATA= data set, the NLINCON statement must be terminated by the / SUMOBS option.
- If the continuous functions should be evaluated separately for each observation in the data set, the NLINCON statement must be terminated by the / EVERYOBS option. One constraint is generated for each observation in the data set.
If the continuous function should be evaluated only once for the entire data set, the NLINCON statement has the same form as the BOUNDS statement. If this constraint does depend on the values of variables in the DATA= data set, it is evaluated using the data of the first observation.

One- or two-sided constraints can be specified in the NLINCON statement. However, equality constraints must be one-sided. The pairs of operators (<, $<=$ ) and (>, $>=$ ) are treated in the same way.

These three statements require the values of the three functions $v_1, v_2, v_3$ to be between zero and ten, and they are equivalent:

   nlincon 0 <= v1-v3,
           v1-v3 <= 10;

   nlincon 0 <= v1-v3 <= 10;

   nlincon 10 >= v1-v3 >= 0;

Also, consider the Rosen-Suzuki problem. It has three nonlinear inequality constraints:

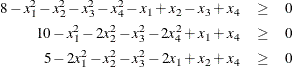
$\begin{eqnarray*} 8 - x_1^2 - x_2^2 - x_3^2 - x_4^2 - x_1 + x_2 - x_3 + x_4 & \geq & 0 \\ 10 - x_1^2 - 2 x_2^2 - x_3^2 - 2 x_4^2 + x_1 + x_4 & \geq & 0 \\ 5 - 2 x_1^2 - x_2^2 - x_3^2 - 2 x_1 + x_2 + x_4 & \geq & 0 \end{eqnarray*}$

These are specified as

   nlincon c1-c3 >= 0;

   c1 = 8 - x1 * x1 - x2 * x2 - x3 * x3 - x4 * x4 -
            x1 + x2 - x3 + x4;
   c2 = 10 - x1 * x1 - 2 * x2 * x2 - x3 * x3 - 2 * x4 * x4 +
            x1 + x4;
   c3 = 5 - 2 * x1 * x1 - x2 * x2 - x3 * x3 - 2 * x1 + x2 + x4;

Note: QUANEW and NMSIMP are the only optimization subroutines that support the NLINCON statement.