The NLP Procedure
- Overview
-
Getting Started

-
Syntax
 Functional SummaryDictionary of OptionsPROC NLP StatementARRAY StatementBOUNDS StatementBY StatementCRPJAC StatementDECVAR StatementGRADIENT StatementHESSIAN StatementINCLUDE StatementJACNLC StatementJACOBIAN StatementLABEL StatementLINCON StatementMATRIX StatementMIN, MAX, and LSQ StatementsMINQUAD and MAXQUAD StatementsNLINCON StatementPROFILE StatementProgram Statements
Functional SummaryDictionary of OptionsPROC NLP StatementARRAY StatementBOUNDS StatementBY StatementCRPJAC StatementDECVAR StatementGRADIENT StatementHESSIAN StatementINCLUDE StatementJACNLC StatementJACOBIAN StatementLABEL StatementLINCON StatementMATRIX StatementMIN, MAX, and LSQ StatementsMINQUAD and MAXQUAD StatementsNLINCON StatementPROFILE StatementProgram Statements -
Details
 Criteria for OptimalityOptimization AlgorithmsFinite-Difference Approximations of DerivativesHessian and CRP Jacobian ScalingTesting the Gradient SpecificationTermination CriteriaActive Set MethodsFeasible Starting PointLine-Search MethodsRestricting the Step LengthComputational ProblemsCovariance MatrixInput and Output Data SetsDisplayed OutputMissing ValuesComputational ResourcesMemory LimitRewriting NLP Models for PROC OPTMODEL
Criteria for OptimalityOptimization AlgorithmsFinite-Difference Approximations of DerivativesHessian and CRP Jacobian ScalingTesting the Gradient SpecificationTermination CriteriaActive Set MethodsFeasible Starting PointLine-Search MethodsRestricting the Step LengthComputational ProblemsCovariance MatrixInput and Output Data SetsDisplayed OutputMissing ValuesComputational ResourcesMemory LimitRewriting NLP Models for PROC OPTMODEL -
Examples

- References
There are three groups of optimization techniques available in PROC NLP. A particular optimizer can be selected with the TECH= option in the PROC NLP statement.
Table 7.2: Karush-Kuhn-Tucker Conditions
|
Algorithm |
TECH= |
|
Linear Complementarity Problem |
LICOMP |
|
Quadratic Active Set Technique |
QUADAS |
|
Trust-Region Method |
TRUREG |
|
Newton-Raphson Method with Line Search |
NEWRAP |
|
Newton-Raphson Method with Ridging |
NRRIDG |
|
Quasi-Newton Methods (DBFGS, DDFP, BFGS, DFP) |
QUANEW |
|
Double Dogleg Method (DBFGS, DDFP) |
DBLDOG |
|
Conjugate Gradient Methods (PB, FR, PR, CD) |
CONGRA |
|
Nelder-Mead Simplex Method |
NMSIMP |
|
Levenberg-Marquardt Method |
LEVMAR |
|
Hybrid Quasi-Newton Methods (DBFGS, DDFP) |
HYQUAN |
Since no single optimization technique is invariably superior to others, PROC NLP provides a variety of optimization techniques that work well in various circumstances. However, it is possible to devise problems for which none of the techniques in PROC NLP can find the correct solution. Moreover, nonlinear optimization can be computationally expensive in terms of time and memory, so care must be taken when matching an algorithm to a problem.
All optimization techniques in PROC NLP use ![]() memory except the conjugate gradient methods, which use only
memory except the conjugate gradient methods, which use only ![]() memory and are designed to optimize problems with many variables.
Since the techniques are iterative, they require the repeated computation of
memory and are designed to optimize problems with many variables.
Since the techniques are iterative, they require the repeated computation of
-
the function value (optimization criterion)
-
the gradient vector (first-order partial derivatives)
-
for some techniques, the (approximate) Hessian matrix (second-order partial derivatives)
-
values of linear and nonlinear constraints
-
the first-order partial derivatives (Jacobian) of nonlinear constraints
However, since each of the optimizers requires different derivatives and supports different types of constraints, some computational efficiencies can be gained. The following table shows, for each optimization technique, which derivatives are needed (FOD: first-order derivatives; SOD: second-order derivatives) and what kinds of constraints (BC: boundary constraints; LIC: linear constraints; NLC: nonlinear constraints) are supported.
|
Algorithm |
FOD |
SOD |
BC |
LIC |
NLC |
|
LICOMP |
- |
- |
x |
x |
- |
|
QUADAS |
- |
- |
x |
x |
- |
|
TRUREG |
x |
x |
x |
x |
- |
|
NEWRAP |
x |
x |
x |
x |
- |
|
NRRIDG |
x |
x |
x |
x |
- |
|
QUANEW |
x |
- |
x |
x |
x |
|
DBLDOG |
x |
- |
x |
x |
- |
|
CONGRA |
x |
- |
x |
x |
- |
|
NMSIMP |
- |
- |
x |
x |
x |
|
LEVMAR |
x |
- |
x |
x |
- |
|
HYQUAN |
x |
- |
x |
x |
- |
It is rare that a problem is submitted to an optimization algorithm “as is.” By making a few changes in your problem, you can reduce its complexity, which would increase the chance of convergence and save execution time.
-
Whenever possible, use linear functions instead of nonlinear functions. PROC NLP will reward you with faster and more accurate solutions.
-
Most optimization algorithms are based on quadratic approximations to nonlinear functions. You should try to avoid the use of functions that cannot be properly approximated by quadratic functions. Try to avoid the use of rational functions.
For example, the constraint
![\[ \frac{\sin (x)}{x+1} > 0 \]](images/ormplpug_nlp0254.png)
should be replaced by the equivalent constraint
![\[ \sin (x)(x+1) > 0 \]](images/ormplpug_nlp0255.png)
and the constraint
![\[ \frac{\sin (x)}{x+1} = 1 \]](images/ormplpug_nlp0256.png)
should be replaced by the equivalent constraint
![\[ \sin (x) - (x+1) = 0 \]](images/ormplpug_nlp0257.png)
-
Try to avoid the use of exponential functions, if possible.
-
If you can reduce the complexity of your function by the addition of a small number of variables, it may help the algorithm avoid stationary points.
-
Provide the best starting point you can. A good starting point leads to better quadratic approximations and faster convergence.
The factors that go into choosing a particular optimizer for a particular problem are complex and may involve trial and error. Several things must be taken into account. First, the structure of the problem has to be considered: Is it quadratic? least squares? Does it have linear or nonlinear constraints? Next, it is important to consider the type of derivatives of the objective function and the constraints that are needed and whether these are analytically tractable or not. This section provides some guidelines for making the right choices.
For many optimization problems, computing the gradient takes more computer time than computing the function value, and computing the Hessian sometimes takes much more computer time and memory than computing the gradient, especially when there are many decision variables. Optimization techniques that do not use the Hessian usually require more iterations than techniques that do use Hessian approximations (such as finite differences or BFGS update) and so are often slower. Techniques that do not use Hessians at all tend to be slow and less reliable.
The derivative compiler is not efficient in the computation of second-order derivatives. For large problems, memory and computer time can be saved by programming your own derivatives using the GRADIENT, JACOBIAN, CRPJAC, HESSIAN, and JACNLC statements. If you are not able to specify first- and second-order derivatives of the objective function, you can rely on finite-difference gradients and Hessian update formulas. This combination is frequently used and works very well for small and medium problems. For large problems, you are advised not to use an optimization technique that requires the computation of second derivatives.
The following provides some guidance for matching an algorithm to a particular problem.
-
-
QUADAS
-
LICOMP
-
-
General Nonlinear Optimization
-
Nonlinear Constraints
-
Only Linear Constraints
-
Small Problems: TRUREG (NEWRAP, NRRIDG) (
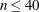 ) where the Hessian matrix is not expensive to compute. Sometimes NRRIDG can be faster than TRUREG, but TRUREG can be more
stable. NRRIDG needs only one matrix with
) where the Hessian matrix is not expensive to compute. Sometimes NRRIDG can be faster than TRUREG, but TRUREG can be more
stable. NRRIDG needs only one matrix with 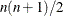 double words; TRUREG and NEWRAP need two such matrices.
double words; TRUREG and NEWRAP need two such matrices.
-
Medium Problems: QUANEW (DBLDOG) (
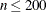 ) where the objective function and the gradient are much faster to evaluate than the Hessian. QUANEW and DBLDOG in general
need more iterations than TRUREG, NRRIDG, and NEWRAP, but each iteration can be much faster. QUANEW and DBLDOG need only the
gradient to update an approximate Hessian. QUANEW and DBLDOG need slightly less memory than TRUREG or NEWRAP (essentially
one matrix with
) where the objective function and the gradient are much faster to evaluate than the Hessian. QUANEW and DBLDOG in general
need more iterations than TRUREG, NRRIDG, and NEWRAP, but each iteration can be much faster. QUANEW and DBLDOG need only the
gradient to update an approximate Hessian. QUANEW and DBLDOG need slightly less memory than TRUREG or NEWRAP (essentially
one matrix with 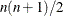 double words).
double words).
-
Large Problems: CONGRA (
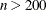 ) where the objective function and the gradient can be computed much faster than the Hessian and where too much memory is
needed to store the (approximate) Hessian. CONGRA in general needs more iterations than QUANEW or DBLDOG, but each iteration
can be much faster. Since CONGRA needs only a factor of
) where the objective function and the gradient can be computed much faster than the Hessian and where too much memory is
needed to store the (approximate) Hessian. CONGRA in general needs more iterations than QUANEW or DBLDOG, but each iteration
can be much faster. Since CONGRA needs only a factor of  double-word memory, many large applications of PROC NLP can be solved only by CONGRA.
double-word memory, many large applications of PROC NLP can be solved only by CONGRA.
-
No Derivatives: NMSIMP (
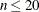 ) where derivatives are not continuous or are very difficult to compute.
) where derivatives are not continuous or are very difficult to compute.
-
-
-
-
Small Problems: LEVMAR (HYQUAN) (
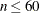 ) where the crossproduct Jacobian matrix is inexpensive to compute. In general, LEVMAR is more reliable, but there are problems
with high residuals where HYQUAN can be faster than LEVMAR.
) where the crossproduct Jacobian matrix is inexpensive to compute. In general, LEVMAR is more reliable, but there are problems
with high residuals where HYQUAN can be faster than LEVMAR.
-
Medium Problems: QUANEW (DBLDOG) (
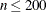 ) where the objective function and the gradient are much faster to evaluate than the crossproduct Jacobian. QUANEW and DBLDOG
in general need more iterations than LEVMAR or HYQUAN, but each iteration can be much faster.
) where the objective function and the gradient are much faster to evaluate than the crossproduct Jacobian. QUANEW and DBLDOG
in general need more iterations than LEVMAR or HYQUAN, but each iteration can be much faster.
-
The QUADAS and LICOMP algorithms can be used to minimize or maximize a quadratic objective function,
subject to linear or boundary constraints
where ![]() ,
, ![]() ,
, ![]() is an
is an ![]() symmetric matrix,
symmetric matrix, ![]() is an
is an ![]() matrix of general linear constraints, and
matrix of general linear constraints, and ![]() . The value of
. The value of ![]() modifies only the value of the objective function, not its derivatives, and the location of the optimizer
modifies only the value of the objective function, not its derivatives, and the location of the optimizer ![]() does not depend on the value of the constant term
does not depend on the value of the constant term ![]() . For QUADAS or LICOMP, the objective function must be specified using the MINQUAD or MAXQUAD statement or using an INQUAD= data set.
. For QUADAS or LICOMP, the objective function must be specified using the MINQUAD or MAXQUAD statement or using an INQUAD= data set.
In this case, derivatives do not need to be specified because the gradient vector
and the ![]() Hessian matrix
Hessian matrix
are easily obtained from the data input.
Simple boundary and general linear constraints can be specified using the BOUNDS or LINCON statement or an INQUAD= or INEST= data set.
The QUADAS algorithm is an active set method that iteratively updates the ![]() decomposition of the matrix
decomposition of the matrix ![]() of active linear constraints and the Cholesky factor of the projected Hessian
of active linear constraints and the Cholesky factor of the projected Hessian ![]() simultaneously. The update of active boundary and linear constraints is done separately; refer to Gill et al. (1984). Here
simultaneously. The update of active boundary and linear constraints is done separately; refer to Gill et al. (1984). Here ![]() is an
is an ![]() orthogonal matrix composed of vectors spanning the null space
orthogonal matrix composed of vectors spanning the null space ![]() of
of ![]() in its first
in its first ![]() columns and range space
columns and range space ![]() in its last
in its last ![]() columns;
columns; ![]() is an
is an ![]() triangular matrix of special form,
triangular matrix of special form, ![]() for
for ![]() , where
, where ![]() is the number of free parameters (
is the number of free parameters (![]() minus the number of active boundary constraints), and
minus the number of active boundary constraints), and ![]() is the number of active linear constraints. The Cholesky factor of the projected Hessian matrix
is the number of active linear constraints. The Cholesky factor of the projected Hessian matrix ![]() and the
and the ![]() decomposition are updated simultaneously when the active set changes.
decomposition are updated simultaneously when the active set changes.
The LICOMP technique solves a quadratic problem as a linear complementarity problem. It can be used only if ![]() is positive (negative) semidefinite for minimization (maximization) and if the parameters are restricted to be positive.
is positive (negative) semidefinite for minimization (maximization) and if the parameters are restricted to be positive.
This technique finds a point that meets the Karush-Kuhn-Tucker conditions by solving the linear complementary problem
with constraints
where
Only the LCEPSILON= option can be used to specify a tolerance used in computations.
The trust region method uses the gradient ![]() and Hessian matrix
and Hessian matrix ![]() and thus requires that the objective function
and thus requires that the objective function ![]() have continuous first- and second-order derivatives inside the feasible region.
have continuous first- and second-order derivatives inside the feasible region.
The trust region method iteratively optimizes a quadratic approximation to the nonlinear objective function within a hyperelliptic
trust region with radius ![]() that constrains the step length corresponding to the quality of the quadratic approximation. The trust region method is implemented
using Dennis, Gay, and Welsch (1981), Gay (1983).
that constrains the step length corresponding to the quality of the quadratic approximation. The trust region method is implemented
using Dennis, Gay, and Welsch (1981), Gay (1983).
The trust region method performs well for small to medium problems and does not require many function, gradient, and Hessian calls. If the computation of the Hessian matrix is computationally expensive, use the UPDATE= option for update formulas (that gradually build the second-order information in the Hessian). For larger problems, the conjugate gradient algorithm may be more appropriate.
The NEWRAP technique uses the gradient ![]() and Hessian matrix
and Hessian matrix ![]() and thus requires that the objective function have continuous first- and second-order derivatives inside the feasible region.
If second-order derivatives are computed efficiently and precisely, the NEWRAP method may perform well for medium to large
problems, and it does not need many function, gradient, and Hessian calls.
and thus requires that the objective function have continuous first- and second-order derivatives inside the feasible region.
If second-order derivatives are computed efficiently and precisely, the NEWRAP method may perform well for medium to large
problems, and it does not need many function, gradient, and Hessian calls.
This algorithm uses a pure Newton step when the Hessian is positive definite and when the Newton step reduces the value of the objective function successfully. Otherwise, a combination of ridging and line search is done to compute successful steps. If the Hessian is not positive definite, a multiple of the identity matrix is added to the Hessian matrix to make it positive definite (Eskow and Schnabel 1991).
In each iteration, a line search is done along the search direction to find an approximate optimum of the objective function. The default line-search method uses quadratic interpolation and cubic extrapolation (LIS=2).
The NRRIDG technique uses the gradient ![]() and Hessian matrix
and Hessian matrix ![]() and thus requires that the objective function have continuous first- and second-order derivatives inside the feasible region.
and thus requires that the objective function have continuous first- and second-order derivatives inside the feasible region.
This algorithm uses a pure Newton step when the Hessian is positive definite and when the Newton step reduces the value of the objective function successfully. If at least one of these two conditions is not satisfied, a multiple of the identity matrix is added to the Hessian matrix. If this algorithm is used for least squares problems, it performs a ridged Gauss-Newton minimization.
The NRRIDG method performs well for small to medium problems and does not need many function, gradient, and Hessian calls. However, if the computation of the Hessian matrix is computationally expensive, one of the (dual) quasi-Newton or conjugate gradient algorithms may be more efficient.
Since NRRIDG uses an orthogonal decomposition of the approximate Hessian, each iteration of NRRIDG can be slower than that of NEWRAP, which works with Cholesky decomposition. However, usually NRRIDG needs fewer iterations than NEWRAP.
The (dual) quasi-Newton method uses the gradient ![]() and does not need to compute second-order derivatives since they are approximated. It works well for medium to moderately
large optimization problems where the objective function and the gradient are much faster to compute than the Hessian, but
in general it requires more iterations than the techniques TRUREG, NEWRAP, and NRRIDG, which compute second-order derivatives.
and does not need to compute second-order derivatives since they are approximated. It works well for medium to moderately
large optimization problems where the objective function and the gradient are much faster to compute than the Hessian, but
in general it requires more iterations than the techniques TRUREG, NEWRAP, and NRRIDG, which compute second-order derivatives.
The QUANEW algorithm depends on whether or not there are nonlinear constraints.
If there are no nonlinear constraints, QUANEW is either
-
the original quasi-Newton algorithm that updates an approximation of the inverse Hessian, or
-
the dual quasi-Newton algorithm that updates the Cholesky factor of an approximate Hessian (default),
depending on the value of the UPDATE= option. For problems with general linear inequality constraints, the dual quasi-Newton methods can be more efficient than the original ones.
Four update formulas can be specified with the UPDATE= option:
- DBFGS
-
performs the dual BFGS (Broyden, Fletcher, Goldfarb, & Shanno) update of the Cholesky factor of the Hessian matrix. This is the default.
- DDFP
-
performs the dual DFP (Davidon, Fletcher, & Powell) update of the Cholesky factor of the Hessian matrix.
- BFGS
-
performs the original BFGS (Broyden, Fletcher, Goldfarb, & Shanno) update of the inverse Hessian matrix.
- DFP
-
performs the original DFP (Davidon, Fletcher, & Powell) update of the inverse Hessian matrix.
In each iteration, a line search is done along the search direction to find an approximate optimum. The default line-search
method uses quadratic interpolation and cubic extrapolation to obtain a step length ![]() satisfying the Goldstein conditions.
One of the Goldstein conditions can be violated if the feasible region defines an upper limit of the step length. Violating
the left-side Goldstein condition can affect the positive definiteness of the quasi-Newton update. In those cases, either
the update is skipped or the iterations are restarted with an identity matrix resulting in the steepest descent or ascent
search direction. Line-search algorithms other than the default one can be specified with the LINESEARCH= option.
satisfying the Goldstein conditions.
One of the Goldstein conditions can be violated if the feasible region defines an upper limit of the step length. Violating
the left-side Goldstein condition can affect the positive definiteness of the quasi-Newton update. In those cases, either
the update is skipped or the iterations are restarted with an identity matrix resulting in the steepest descent or ascent
search direction. Line-search algorithms other than the default one can be specified with the LINESEARCH= option.
The algorithm used for nonlinearly constrained quasi-Newton optimization is an efficient modification of Powell’s (1978a, 1982b) Variable Metric Constrained WatchDog (VMCWD) algorithm. A similar but older algorithm (VF02AD) is part of the Harwell library. Both VMCWD and VF02AD use Fletcher’s VE02AD algorithm (part of the Harwell library) for positive-definite quadratic programming. The PROC NLP QUANEW implementation uses a quadratic programming subroutine that updates and downdates the approximation of the Cholesky factor when the active set changes. The nonlinear QUANEW algorithm is not a feasible-point algorithm, and the value of the objective function need not decrease (minimization) or increase (maximization) monotonically. Instead, the algorithm tries to reduce a linear combination of the objective function and constraint violations, called the merit function.
The following are similarities and differences between this algorithm and the VMCWD algorithm:
-
A modification of this algorithm can be performed by specifying VERSION=1, which replaces the update of the Lagrange vector
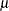 with the original update of Powell (1978a, 1978b) that is used in VF02AD. This can be helpful for some applications with linearly dependent active constraints.
with the original update of Powell (1978a, 1978b) that is used in VF02AD. This can be helpful for some applications with linearly dependent active constraints.
-
If the VERSION option is not specified or if VERSION=2 is specified, the evaluation of the Lagrange vector
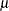 is performed in the same way as Powell (1982b) describes.
is performed in the same way as Powell (1982b) describes.
-
Instead of updating an approximate Hessian matrix, this algorithm uses the dual BFGS (or DFP) update that updates the Cholesky factor of an approximate Hessian. If the condition of the updated matrix gets too bad, a restart is done with a positive diagonal matrix. At the end of the first iteration after each restart, the Cholesky factor is scaled.
-
The Cholesky factor is loaded into the quadratic programming subroutine, automatically ensuring positive definiteness of the problem. During the quadratic programming step, the Cholesky factor of the projected Hessian matrix
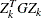 and the
and the 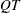 decomposition are updated simultaneously when the active set changes. Refer to Gill et al. (1984) for more information.
decomposition are updated simultaneously when the active set changes. Refer to Gill et al. (1984) for more information.
-
The line-search strategy is very similar to that of Powell (1982b). However, this algorithm does not call for derivatives during the line search, so the algorithm generally needs fewer derivative calls than function calls. VMCWD always requires the same number of derivative and function calls. Sometimes Powell’s line-search method uses steps that are too long. In these cases, use the INSTEP= option to restrict the step length
 .
.
-
The watchdog strategy is similar to that of Powell (1982b); however, it does not return automatically after a fixed number of iterations to a former better point. A return here is further delayed if the observed function reduction is close to the expected function reduction of the quadratic model.
-
The Powell termination criterion still is used (as FCONV2) but the QUANEW implementation uses two additional termination criteria (GCONV and ABSGCONV).
The nonlinear QUANEW algorithm needs the Jacobian matrix of the first-order derivatives (constraints normals) of the constraints
![]() .
.
You can specify two update formulas with the UPDATE= option:
This algorithm uses its own line-search technique. No options or parameters (except the INSTEP= option) controlling the line search in the other algorithms apply here. In several applications, large steps in the first
iterations were troublesome. You can use the INSTEP= option to impose an upper bound for the step length ![]() during the first five iterations. You may also use the INHESSIAN= option
to specify a different starting approximation for the Hessian. Choosing simply the INHESSIAN option will use the Cholesky factor of a (possibly ridged) finite-difference approximation of the Hessian to initialize the
quasi-Newton update process. The values of the LCSINGULAR=, LCEPSILON=, and LCDEACT= options,
which control the processing of linear and boundary constraints, are valid only for the quadratic programming subroutine used
in each iteration of the nonlinear constraints QUANEW algorithm.
during the first five iterations. You may also use the INHESSIAN= option
to specify a different starting approximation for the Hessian. Choosing simply the INHESSIAN option will use the Cholesky factor of a (possibly ridged) finite-difference approximation of the Hessian to initialize the
quasi-Newton update process. The values of the LCSINGULAR=, LCEPSILON=, and LCDEACT= options,
which control the processing of linear and boundary constraints, are valid only for the quadratic programming subroutine used
in each iteration of the nonlinear constraints QUANEW algorithm.
The double dogleg optimization method combines the ideas of the quasi-Newton and trust region methods. The double dogleg algorithm
computes in each iteration the step ![]() as a linear combination of the steepest descent or ascent search direction
as a linear combination of the steepest descent or ascent search direction ![]() and a quasi-Newton search direction
and a quasi-Newton search direction ![]() :
:
The step is requested to remain within a prespecified trust region radius; refer to Fletcher (1987, p. 107). Thus, the DBLDOG subroutine uses the dual quasi-Newton update but does not perform a line search. Two update formulas can be specified with the UPDATE= option:
The double dogleg optimization technique works well for medium to moderately large optimization problems where the objective function and the gradient are much faster to compute than the Hessian. The implementation is based on Dennis and Mei (1979) and Gay (1983) but is extended for dealing with boundary and linear constraints. DBLDOG generally needs more iterations than the techniques TRUREG, NEWRAP, or NRRIDG that need second-order derivatives, but each of the DBLDOG iterations is computationally cheap. Furthermore, DBLDOG needs only gradient calls for the update of the Cholesky factor of an approximate Hessian.
Second-order derivatives are not used by CONGRA. The CONGRA algorithm can be expensive in function and gradient calls but
needs only ![]() memory for unconstrained optimization. In general, many iterations are needed to obtain a precise solution, but each of the
CONGRA iterations is computationally cheap. Four different update formulas for generating the conjugate directions can be
specified using the UPDATE= option:
memory for unconstrained optimization. In general, many iterations are needed to obtain a precise solution, but each of the
CONGRA iterations is computationally cheap. Four different update formulas for generating the conjugate directions can be
specified using the UPDATE= option:
The default value is UPDATE=PB, since it behaved best in most test examples. You are advised to avoid the option UPDATE=CD, a it behaved worst in most test examples.
The CONGRA subroutine should be used for optimization problems with large ![]() .
For the unconstrained or boundary constrained case, CONGRA needs only
.
For the unconstrained or boundary constrained case, CONGRA needs only ![]() bytes of working memory, whereas all other optimization methods require order
bytes of working memory, whereas all other optimization methods require order ![]() bytes of working memory. During
bytes of working memory. During ![]() successive iterations, uninterrupted by restarts or changes in the working set, the conjugate gradient algorithm computes
a cycle of
successive iterations, uninterrupted by restarts or changes in the working set, the conjugate gradient algorithm computes
a cycle of ![]() conjugate search directions. In each iteration, a line search is done along the search direction to find an approximate optimum
of the objective function. The default line-search method uses quadratic interpolation and cubic extrapolation to obtain a
step length
conjugate search directions. In each iteration, a line search is done along the search direction to find an approximate optimum
of the objective function. The default line-search method uses quadratic interpolation and cubic extrapolation to obtain a
step length ![]() satisfying the Goldstein conditions.
One of the Goldstein conditions can be violated if the feasible region defines an upper limit for the step length. Other line-search
algorithms can be specified with the LINESEARCH= option.
satisfying the Goldstein conditions.
One of the Goldstein conditions can be violated if the feasible region defines an upper limit for the step length. Other line-search
algorithms can be specified with the LINESEARCH= option.
The Nelder-Mead simplex method does not use any derivatives and does not assume that the objective function has continuous
derivatives. The objective function itself needs to be continuous. This technique requires a large number of function evaluations.
It is unlikely to give accurate results for ![]() .
.
Depending on the kind of constraints, one of the following Nelder-Mead simplex algorithms is used:
-
unconstrained or only boundary constrained problems
The original Nelder-Mead simplex algorithm is implemented and extended to boundary constraints. This algorithm does not compute the objective for infeasible points. This algorithm is automatically invoked if the LINCON or NLINCON statement is not specified.
-
general linearly constrained or nonlinearly constrained problems
A slightly modified version of Powell’s (1992) COBYLA (Constrained Optimization BY Linear Approximations) implementation is used. This algorithm is automatically invoked if either the LINCON or the NLINCON statement is specified.
The original Nelder-Mead algorithm cannot be used for general linear or nonlinear constraints but can be faster for the unconstrained or boundary constrained case. The original Nelder-Mead algorithm changes the shape of the simplex adapting the nonlinearities of the objective function which contributes to an increased speed of convergence. The two NMSIMP subroutines use special sets of termination criteria. For more details, refer to the section Termination Criteria.
Powell’s COBYLA algorithm is a sequential trust region algorithm (originally with a monotonically decreasing radius ![]() of a spherical trust region) that tries to maintain a regular-shaped simplex over the iterations. A small modification was
made to the original algorithm that permits an increase of the trust region radius
of a spherical trust region) that tries to maintain a regular-shaped simplex over the iterations. A small modification was
made to the original algorithm that permits an increase of the trust region radius ![]() in special situations. A sequence of iterations is performed with a constant trust region radius
in special situations. A sequence of iterations is performed with a constant trust region radius ![]() until the computed objective function reduction is much less than the predicted reduction. Then, the trust region radius
until the computed objective function reduction is much less than the predicted reduction. Then, the trust region radius
![]() is reduced. The trust region radius is increased only if the computed function reduction is relatively close to the predicted
reduction and the simplex is well-shaped. The start radius
is reduced. The trust region radius is increased only if the computed function reduction is relatively close to the predicted
reduction and the simplex is well-shaped. The start radius ![]() and the final radius
and the final radius ![]() can be specified using
can be specified using ![]() =INSTEP and
=INSTEP and ![]() =ABSXTOL. The convergence to small values of
=ABSXTOL. The convergence to small values of ![]() (high precision) may take many calls of the function and constraint modules and may result in numerical problems. There are
two main reasons for the slow convergence of the COBYLA algorithm:
(high precision) may take many calls of the function and constraint modules and may result in numerical problems. There are
two main reasons for the slow convergence of the COBYLA algorithm:
-
Only linear approximations of the objective and constraint functions are used locally.
-
Maintaining the regular-shaped simplex and not adapting its shape to nonlinearities yields very small simplices for highly nonlinear functions (for example, fourth-order polynomials).
The Levenberg-Marquardt method is a modification of the trust region method for nonlinear least squares problems and is implemented as in Moré (1978).
This is the recommended algorithm for small to medium least squares problems. Large least squares problems can be transformed
into minimization problems, which can be processed with conjugate gradient or (dual) quasi-Newton techniques. In each iteration,
LEVMAR solves a quadratically constrained quadratic minimization problem that restricts the step to stay at the surface of
or inside an ![]() - dimensional elliptical (or spherical) trust region. In each iteration, LEVMAR uses the crossproduct Jacobian matrix
- dimensional elliptical (or spherical) trust region. In each iteration, LEVMAR uses the crossproduct Jacobian matrix ![]() as an approximate Hessian matrix.
as an approximate Hessian matrix.
In each iteration of one of the Fletcher and Xu (1987) (refer also to Al-Baali and Fletcher (1985,1986)) hybrid quasi-Newton methods, a criterion is used to decide whether a Gauss-Newton or a dual quasi-Newton search direction is appropriate. The VERSION= option can be used to choose one of three criteria (HY1, HY2, HY3) proposed by Fletcher and Xu (1987). The default is VERSION=2; that is, HY2. In each iteration, HYQUAN computes the crossproduct Jacobian (used for the Gauss-Newton step), updates the Cholesky factor of an approximate Hessian (used for the quasi-Newton step), and does a line search to compute an approximate minimum along the search direction. The default line-search technique used by HYQUAN is especially designed for least squares problems (refer to Lindström and Wedin (1984) and Al-Baali and Fletcher (1986)). Using the LINESEARCH= option you can choose a different line-search algorithm than the default one.
Two update formulas can be specified with the UPDATE= option:
The HYQUAN subroutine needs about the same amount of working memory as the LEVMAR algorithm. In most applications, LEVMAR seems to be superior to HYQUAN, and using HYQUAN is recommended only when problems are experienced with the performance of LEVMAR.