The NLP Procedure

Computational Resources

Since nonlinear optimization is an iterative process that depends on many factors, it is difficult to estimate how much computer time is necessary to compute an optimal solution satisfying one of the termination criteria. The MAXTIME=, MAXITER=, and MAXFUNC= options can be used to restrict the amount of real time, the number of iterations, and the number of function calls in a single run of PROC NLP.

In each iteration $k$ , the NRRIDG and LEVMAR techniques use symmetric Householder transformations to decompose the $n \times n$ Hessian (crossproduct Jacobian) matrix $G$ ,

$G = V^ T T V \: , \quad V \mbox{ orthogonal} , \quad T \mbox{ tridiagonal}$

to compute the (Newton) search direction $s$ :

$s^{(k)} = - G^{(k-1)} g^{(k)} \: , \quad k=1,2,3,\ldots$

The QUADAS, TRUREG, NEWRAP, and HYQUAN techniques use the Cholesky decomposition to solve the same linear system while computing the search direction. The QUANEW, DBLDOG, CONGRA, and NMSIMP techniques do not need to invert or decompose a Hessian or crossproduct Jacobian matrix and thus require fewer computational resources then the first group of techniques.

The larger the problem, the more time is spent computing function values and derivatives. Therefore, many researchers compare optimization techniques by counting and comparing the respective numbers of function, gradient, and Hessian (crossproduct Jacobian) evaluations. You can save computer time and memory by specifying derivatives (using the GRADIENT, JACOBIAN, CRPJAC, or HESSIAN statement) since you will typically produce a more efficient representation than the internal derivative compiler.

Finite-difference approximations of the derivatives are expensive since they require additional function or gradient calls.

Forward-difference formulas:
- First-order derivatives: $n$ additional function calls are needed.
- Second-order derivatives based on function calls only: for a dense Hessian, 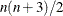$n(n+3)/2$ additional function calls are needed.
- Second-order derivatives based on gradient calls: $n$ additional gradient calls are needed.
Central-difference formulas:
- First-order derivatives: 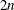$2n$ additional function calls are needed.
- Second-order derivatives based on function calls only: for a dense Hessian, 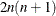$2n(n+1)$ additional function calls are needed.
- Second-order derivatives based on gradient: 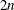$2n$ additional gradient calls are needed.

Many applications need considerably more time for computing second-order derivatives (Hessian matrix) than for first-order derivatives (gradient). In such cases, a (dual) quasi-Newton or conjugate gradient technique is recommended, which does not require second-order derivatives.

The following table shows for each optimization technique which derivatives are needed (FOD: first-order derivatives; SOD: second-order derivatives), what kinds of constraints are supported (BC: boundary constraints; LIC: linear constraints), and the minimal memory (number of double floating point numbers) required. For various reasons, there are additionally about $7n+m$ double floating point numbers needed.

Quadratic Programming	FOD	SOD	BC	LIC	Memory
LICOMP	-	-	x	x	$18n + 3nn$
QUADAS	-	-	x	x	$1n + 2nn/2$
General Optimization	FOD	SOD	BC	LIC	Memory
TRUREG	x	x	x	x	$4n + 2nn/2$
NEWRAP	x	x	x	x	$2n + 2nn/2$
NRRIDG	x	x	x	x	$6n + nn/2$
QUANEW	x	-	x	x	$1n + nn/2$
DBLDOG	x	-	x	x	$7n + nn/2$
CONGRA	x	-	x	x	$3n$
NMSIMP	-	-	x	x	$4n + nn$
Least Squares	FOD	SOD	BC	LIC	Memory
LEVMAR	x	-	x	x	$6n + nn/2$
HYQUAN	x	-	x	x	$2n + nn/2 + 3m$

Notes:

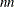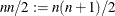Here, $n$ denotes the number of parameters, $nn$ the squared number of parameters, and $nn/2 := n(n+1)/2$ .
The value of 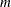$m$ is the product of the number of functions specified in the MIN, MAX, or LSQ statement and the maximum number of observations in each BY group of a DATA= input data set. The following table also contains the number $v$ of variables in the DATA= data set that are used in the program statements.
For a diagonal Hessian matrix, the 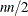$nn/2$ term in QUADAS, TRUREG, NEWRAP, and NRRIDG is replaced by $n$ .
If the TRUREG, NRRIDG, or NEWRAP method is used to minimize a least squares problem, the second derivatives are replaced by the crossproduct Jacobian matrix.
The memory needed by the TECH=NONE specification depends on the output specifications (typically, it needs 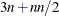$3n+nn/2$ double floating point numbers and an additional 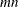$mn$ if the Jacobian matrix is required).

The total amount of memory needed to run an optimization technique consists of the technique-specific memory listed in the preceding table, plus additional blocks of memory as shown in the following table.

	double	int	long	8byte
Basic Requirement	$7n+m$	$n$	$3n$	$n+m$
DATA= data set	$v$	-	-	$v$
JACOBIAN statement	$m(n+2)$	-	-	-
CRPJAC statement	$nn/2$	-	-	-
HESSIAN statement	$nn/2$	-	-	-
COV= option	$(2*)nn/2 + n$	-	-	-
Scaling vector	$n$	-	-	-
BOUNDS statement	$2n$	$n$	-	-
Bounds in INEST=	$2n$	-	-	-
LINCON and TRUREG	$c(n+1)+nn+ nn/2+4n$	$3c$	-	-
LINCON and other	$c(n+1)+nn+2nn/2+4n$	$3c$	-	-

Notes:

For TECH=LICOMP, the total amount of memory needed for the linear or boundary constrained case is 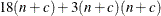$18(n + c) + 3(n + c)(n + c)$ , where $c$ is the number of constraints.
The amount of memory needed to specify derivatives with a GRADIENT, JACOBIAN, CRPJAC, or HESSIAN statement (shown in this table) is small compared to that needed for using the internal function compiler to compute the derivatives. This is especially so for second-order derivatives.
If the CONGRA technique is used, specifying the GRADCHECK=DETAIL option requires an additional 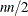$nn/2$ double floating point numbers to store the finite-difference Hessian matrix.