The HTSNP Procedure (Experimental)

Statistical Computations

Subsections:

Diversity
Evaluating Sets of htSNPs

Diversity

Let $f_1,\ldots ,f_ n$ represent the proportional frequencies of the $n$ unique $M$ -locus haplotypes in the input data set. The locus or allelic diversity $D_1,\ldots ,D_ M$ for the $M$ individual loci and the overall haplotype diversity $D$ can be calculated as

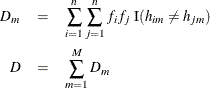
$\begin{eqnarray*} D_ m & = & \sum _{i=1}^ n \sum _{j=1}^ n f_ i f_ j \mbox{ I}(h_{im} \neq h_{jm}) \\ D & = & \sum _{m=1}^ M D_ m \\ \end{eqnarray*}$

where $h_{im}$ is the allele of the $i$ th haplotype observed at the $m$ th locus and the indicator function $\mbox{I}()$ equals 1 when true and 0 otherwise (Clayton, 2002).

Based on a selected subset of $k$ SNPs, the $n$ observed haplotypes can be partitioned into $T$ distinct groups. Let $\mathcal{T}_ t$ represent the set of haplotypes in group $t=1,\ldots ,T$ , where each set contains all haplotypes that have identical alleles at the $k$ selected loci. The residual diversity is calculated by Clayton (2002) by summing the within-group diversity over the $T$ groups, again both for the individual loci and over all haplotypes:

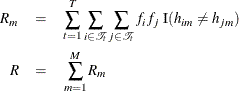
$\begin{eqnarray*} R_ m & = & \sum _{t=1}^ T \sum _{i\in \mathcal{T}_ t} \sum _{j\in \mathcal{T}_ t} f_ i f_ j \mbox{ I}(h_{im} \neq h_{jm}) \\ R & = & \sum _{m=1}^ M R_ m \\ \end{eqnarray*}$

where $m=1,\ldots ,M$ . Note that $R_ m=0$ if locus $m$ is one of the $k$ selected SNPs.

Evaluating Sets of htSNPs

One of two criteria for finding the optimal set of htSNPs can be selected with the CRITERION= option. Using the diversity measures previously defined, the proportion of diversity explained (PDE) by a candidate SNP set can be calculated to evaluate the goodness of the set (Clayton, 2002):

$\mbox{PDE}=1-\frac{R}{D}$

The higher (that is, closer to 1) the value of PDE is, the better the set of htSNPs is for explaining the diversity among the haplotypes.

Alternatively, the approach of Stram et al. (2003) is implemented when CRITERION=RSQH. For these computations, define $\delta _ h(\mathcal{H}_ i)$ to be the actual number of copies of haplotype $h$ that an individual with the $M$ -locus haplotype pair $\mathcal{H}_ i$ (usually unknown) and genotype $G_ i$ carries. Assuming Hardy-Weinberg equilibrium, this can be estimated as

$E[\delta _ h(\mathcal{H}_ i)|G_ i] = \frac{ \sum _{j\in H_ i} \delta _ h (h_ j, h_ j^{ci})f_ j f_ j^{ci}}{\sum _{j\in H_ i}f_ j f_ j^{ci}}$

where $H_ i$ is the set of haplotype pairs, $h_ j$ and its complement $h_ j^{ci}$ , compatible with genotype $G_ i$ . Then $R_ h^2$ can be defined as follows for each haplotype $h$ :

$R^2_ h = \frac{\mathrm{Var}\{ E[\delta _ h(\mathcal{H}_ i)|G_ i]\} }{2f_ h(1-f_ h)} = \frac{\sum _ i\{ [E(\delta _ h (\mathcal{H}_ i)|G_ i)]^2 \Pr (G_ i)\} -4f_ h^2}{2f_ h(1-f_ h)}$

with $G_ i$ representing each possible $k$ -locus genotype at the selected SNPs and $\Pr (G_ i)=\sum _{j\in H_ i} f_ j f_ j^{ci}$ . The set of $k$ SNPs with the highest (that is, closest to 1) value of $\min _ h R^2_ h$ is selected as the best set of htSNPs, for it optimizes the predictability of the common haplotypes (Stram et al., 2003).