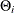The UCM Procedure
- Overview
-
Getting Started

-
Syntax
 Functional SummaryPROC UCM StatementAUTOREG StatementBLOCKSEASON StatementBY StatementCYCLE StatementDEPLAG StatementESTIMATE StatementFORECAST StatementID StatementIRREGULAR StatementLEVEL StatementMODEL StatementNLOPTIONS StatementOUTLIER StatementPERFORMANCE StatementRANDOMREG StatementSEASON StatementSLOPE StatementSPLINEREG StatementSPLINESEASON Statement
Functional SummaryPROC UCM StatementAUTOREG StatementBLOCKSEASON StatementBY StatementCYCLE StatementDEPLAG StatementESTIMATE StatementFORECAST StatementID StatementIRREGULAR StatementLEVEL StatementMODEL StatementNLOPTIONS StatementOUTLIER StatementPERFORMANCE StatementRANDOMREG StatementSEASON StatementSLOPE StatementSPLINEREG StatementSPLINESEASON Statement -
Details

-
Examples

- References
IRREGULAR Statement
-
IRREGULAR <options>;
The IRREGULAR statement includes an irregular component in the model. There can be at most one IRREGULAR statement in the
model specification. The irregular component corresponds to the overall random error 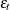 in the model. By default the irregular component is modeled as white noise—that is, as a sequence of independent, identically
distributed, zero-mean, Gaussian random variables. However, you can also model it as an autoregressive moving average (ARMA)
process. The options for specifying an ARMA model for the irregular component are given in a separate subsection: ARMA Specification.
in the model. By default the irregular component is modeled as white noise—that is, as a sequence of independent, identically
distributed, zero-mean, Gaussian random variables. However, you can also model it as an autoregressive moving average (ARMA)
process. The options for specifying an ARMA model for the irregular component are given in a separate subsection: ARMA Specification.
The options in this statement enable you to specify the model for the irregular component and to output its estimates. Two examples of the IRREGULAR statement are given next. In the first example the statement is in its simplest form, resulting in the inclusion of an irregular component that is white noise with unknown variance:
irregular;
The following statement provides a starting value for the white noise variance 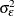 to be used in the nonlinear parameter estimation process. It also requests the printing of smoothed estimates of
to be used in the nonlinear parameter estimation process. It also requests the printing of smoothed estimates of 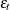 . The smoothed irregulars are useful in model diagnostics.
. The smoothed irregulars are useful in model diagnostics.
irregular variance=4 print=smooth;
ARMA Specification
This section details the options for specifying an ARMA model for the irregular component. The specification of ARMA models requires some notation, which is explained first.
Let B denote the backshift operator—that is, for any sequence 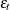 ,
, 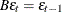 . The higher powers of B represent larger shifts (for example,
. The higher powers of B represent larger shifts (for example, 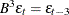 ). A random sequence
). A random sequence 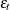 follows a zero-mean ARMA(p,q)
follows a zero-mean ARMA(p,q) (P,Q)
(P,Q) model with nonseasonal autoregressive order p, seasonal autoregressive order P, nonseasonal moving average order q, and seasonal moving average order Q, if it satisfies the following difference equation specified in terms of the polynomials in the backshift operator where
model with nonseasonal autoregressive order p, seasonal autoregressive order P, nonseasonal moving average order q, and seasonal moving average order Q, if it satisfies the following difference equation specified in terms of the polynomials in the backshift operator where
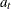 is a white noise sequence and s is the season length:
is a white noise sequence and s is the season length:
![\[ \phi (B) \Phi (B^ s) \epsilon _ t = \theta (B) \Theta (B^ s) a_ t \]](images/etsug_ucm0054.png)
The polynomials 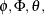 and
and 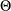 are of orders p, P, q, and Q, respectively, which can be any nonnegative integers. The season length s must be a positive integer. For example,
are of orders p, P, q, and Q, respectively, which can be any nonnegative integers. The season length s must be a positive integer. For example, 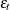 satisfies an ARMA(1,1) model (that is,
satisfies an ARMA(1,1) model (that is, 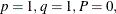 and
and 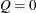 ) if
) if
![\[ \epsilon _ t = \phi _{1} \epsilon _{t-1} + a_ t - \theta _{1} a_{t-1} \]](images/etsug_ucm0059.png)
for some coefficients 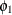 and
and 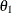 and a white noise sequence
and a white noise sequence 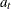 . Similarly
. Similarly 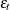 satisfies an ARMA(1,1)
satisfies an ARMA(1,1) (1,1)
(1,1)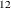 model if
model if
![\[ \epsilon _ t = \phi _{1} \epsilon _{t-1} + \Phi _{1} \epsilon _{t-12} - \phi _{1} \Phi _{1} \epsilon _{t-13} + a_ t - \theta _{1} a_{t-1} - \Theta _{1} a_{t-12} + \theta _{1} \Theta _{1} a_{t-13} \]](images/etsug_ucm0062.png)
for some coefficients 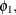
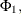
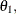 and
and 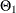 and a white noise sequence
and a white noise sequence 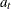 . The ARMA process is stationary and invertible if the defining polynomials
. The ARMA process is stationary and invertible if the defining polynomials 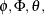 and
and 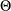 have all their roots outside the unit circle—that is, their absolute values are strictly larger than 1.0. It is assumed that
the ARMA model specified for the irregular component is stationary and invertible—that is, the coefficients of the polynomials
have all their roots outside the unit circle—that is, their absolute values are strictly larger than 1.0. It is assumed that
the ARMA model specified for the irregular component is stationary and invertible—that is, the coefficients of the polynomials
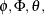 and
and 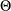 are constrained so that the stationarity and invertibility conditions are satisfied. The unknown coefficients of these polynomials
become part of the model parameter vector that is estimated using the data.
are constrained so that the stationarity and invertibility conditions are satisfied. The unknown coefficients of these polynomials
become part of the model parameter vector that is estimated using the data.
The notation for a closely related class of models, autoregressive integrated moving average (ARIMA) models, is also given
here. A random sequence 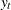 is said to follow an ARIMA(p,d,q)
is said to follow an ARIMA(p,d,q) (P,D,Q)
(P,D,Q) model if, for some nonnegative integers d and D, the differenced series
model if, for some nonnegative integers d and D, the differenced series 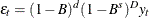 follows an ARMA(p,q)
follows an ARMA(p,q) (P,Q)
(P,Q) model. The integers d and D are called nonseasonal and seasonal differencing orders, respectively. You can specify ARIMA models by using the DEPLAG
statement for specifying the differencing orders and by using the IRREGULAR statement for the ARMA specification. See Example 41.8 for an example of ARIMA(0,1,1)
model. The integers d and D are called nonseasonal and seasonal differencing orders, respectively. You can specify ARIMA models by using the DEPLAG
statement for specifying the differencing orders and by using the IRREGULAR statement for the ARMA specification. See Example 41.8 for an example of ARIMA(0,1,1) (0,1,1)
(0,1,1)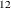 model specification. Brockwell and Davis (1991) can be consulted for additional information about ARIMA models.
model specification. Brockwell and Davis (1991) can be consulted for additional information about ARIMA models.
You can use options of the IRREGULAR statement to specify the desired ARMA model and to request printed and graphical output. A few examples of the IRREGULAR statement are given next.
The following statement specifies an irregular component that is modeled as an ARMA(1,1) process. It also requests plotting its smoothed estimate.
irregular p=1 q=1 plot=smooth;
The following statement specifies an ARMA(1,1) (1,1)
(1,1) model. It also fixes the coefficient of the first-order seasonal moving average polynomial to 0.1. The other coefficients
and the white noise variance are estimated using the data.
model. It also fixes the coefficient of the first-order seasonal moving average polynomial to 0.1. The other coefficients
and the white noise variance are estimated using the data.
irregular p=1 sp=1 q=1 sq=1 s=12 sma=0.1 noest=(sma);
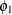
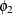
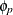
![\[ \phi (B) = 1 - \phi _1 B - \ldots - \phi _{p} B^ p \]](images/etsug_ucm0071.png)
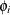
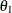
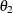
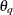
![\[ \theta (B) = 1 - \theta _1 B - \ldots - \theta _{q} B^ q \]](images/etsug_ucm0076.png)
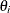
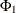
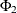
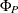
![\[ \Phi (B^ s) = 1 - \Phi _1 B^ s - \ldots - \Phi _{P} B^{s P} \]](images/etsug_ucm0081.png)
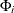
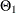
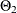
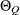
![\[ \Theta (B^ s) = 1 - \Theta _1 B^ s - \ldots - \Theta _{Q} B^{s Q} \]](images/etsug_ucm0086.png)