The UCM Procedure
- Overview
-
Getting Started

-
Syntax
 Functional SummaryPROC UCM StatementAUTOREG StatementBLOCKSEASON StatementBY StatementCYCLE StatementDEPLAG StatementESTIMATE StatementFORECAST StatementID StatementIRREGULAR StatementLEVEL StatementMODEL StatementNLOPTIONS StatementOUTLIER StatementPERFORMANCE StatementRANDOMREG StatementSEASON StatementSLOPE StatementSPLINEREG StatementSPLINESEASON Statement
Functional SummaryPROC UCM StatementAUTOREG StatementBLOCKSEASON StatementBY StatementCYCLE StatementDEPLAG StatementESTIMATE StatementFORECAST StatementID StatementIRREGULAR StatementLEVEL StatementMODEL StatementNLOPTIONS StatementOUTLIER StatementPERFORMANCE StatementRANDOMREG StatementSEASON StatementSLOPE StatementSPLINEREG StatementSPLINESEASON Statement -
Details

-
Examples

- References
Example 41.8 ARIMA Modeling
This example shows how you can use the UCM procedure for ARIMA modeling. The parameter estimates and predictions for ARIMA
models obtained by using PROC UCM will be close to those obtained by using PROC ARIMA (in the presence of the ML option in
its ESTIMATE statement) if the model is stationary or if the model is nonstationary and there are no missing values in the
data. For more information about the ARIMA procedure, see Chapter 8: The ARIMA Procedure. However, if there are missing values in the data and the model is nonstationary, then the UCM and ARIMA procedures can produce
significantly different parameter estimates and predictions. An article by Kohn and Ansley (1986) suggests a statistically sound method of estimation, prediction, and interpolation for nonstationary ARIMA models with missing
data. This method is based on an algorithm that is equivalent to the Kalman filtering and smoothing algorithm used in the
UCM procedure. The results of an illustrative example in their article are reproduced here using the UCM procedure. In this
example an ARIMA(0,1,1) (0,1,1)
(0,1,1)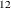 model is applied to the logarithm of the
model is applied to the logarithm of the air series in the sashelp.air data set. Four different missing value patterns are considered to highlight different aspects of the problem:
-
Data1. The full data set of 144 observations.
-
Data2. The set of 78 observations that omit January through November in each of the last 6 years.
-
Data3. The data set with the 5 observations July 1949, June, July, and August 1957, and July 1960 missing.
-
Data4. The data set with all July observations missing and June and August 1957 also missing.
The following DATA steps create these data sets:
data Data1;
set sashelp.air;
logair = log(air);
run;
data Data2;
set data1;
if year(date) >= 1955 and month(date) < 12 then logair = .;
run;
data Data3;
set data1;
if (year(date) = 1949 and month(date) = 7) then logair = .;
if ( year(date) = 1957 and
(month(date) = 6 or month(date) = 7 or month(date) = 8))
then logair = .;
if (year(date) = 1960 and month(date) = 7) then logair = .;
run;
data Data4;
set data1;
if month(date) = 7 then logair = .;
if year(date) = 1957 and (month(date) = 6 or month(date) = 8)
then logair = .;
run;
The following statements specify the ARIMA model for the
model for the logair series in the first data set (Data1):
proc ucm data=Data1; id date interval=month; model logair; irregular q=1 sq=1 s=12; deplag lags=(1)(12) phi=1 1 noest; estimate outest=est1; forecast outfor=for1; run;
Note that the moving average part of the model is specified by using the Q=, SQ=, and S= options in the IRREGULAR statement
and the differencing operator,  , is specified by using the DEPLAG statement. The model does not contain an intercept term; therefore no LEVEL statement is
needed. The parameter estimates are saved in a data set
, is specified by using the DEPLAG statement. The model does not contain an intercept term; therefore no LEVEL statement is
needed. The parameter estimates are saved in a data set EST1 by using the OUTEST= option in the ESTIMATE statement and the forecasts and the component estimates are saved in a data set
FOR1 by using the OUTFOR= option in the FORECAST statement. The same analysis is performed on the other three data sets, but is
not shown here.
Output 41.8.1 resembles Table 1 in Kohn and Ansley (1986). This table is generated by merging the parameter estimates from the four analyses. Only the moving average parameter estimates
and their standard errors are reported. The columns EST1 and STD1 correspond to the estimates for Data1. The parameter estimates and their standard errors for other three data sets are similarly named. Note that the parameter
estimates closely match the parameter estimates in the article. However, their standard errors differ slightly. This difference
could be the result of different ways of computing the Hessian at the optimum. The white noise error variance estimates are
not reported here, but they agree quite closely with those in the article.
Output 41.8.1: Data Sets 1–4: Parameter Estimates and Standard Errors
Output 41.8.2 resembles Table 2 in Kohn and Ansley (1986). It contains forecasts and their standard errors for the four data sets. The numbers are very close to those in the article.
Output 41.8.2: Data Sets 1–4: Forecasts and Standard Errors
| DATE | for1 | std1 | for2 | std2 | for3 | std3 | for4 | std4 |
|---|---|---|---|---|---|---|---|---|
| JAN61 | 6.110 | 0.037 | 6.084 | 0.052 | 6.110 | 0.037 | 6.111 | 0.037 |
| FEB61 | 6.054 | 0.043 | 6.091 | 0.058 | 6.054 | 0.043 | 6.055 | 0.043 |
| MAR61 | 6.172 | 0.048 | 6.247 | 0.063 | 6.173 | 0.048 | 6.174 | 0.048 |
| APR61 | 6.199 | 0.053 | 6.205 | 0.068 | 6.199 | 0.053 | 6.200 | 0.052 |
| MAY61 | 6.233 | 0.057 | 6.199 | 0.072 | 6.232 | 0.058 | 6.233 | 0.056 |
| JUN61 | 6.369 | 0.061 | 6.308 | 0.076 | 6.367 | 0.062 | 6.368 | 0.060 |
| JUL61 | 6.507 | 0.065 | 6.409 | 0.079 | 6.497 | 0.067 | . | . |
| AUG61 | 6.503 | 0.069 | 6.414 | 0.082 | 6.503 | 0.069 | 6.503 | 0.067 |
| SEP61 | 6.325 | 0.072 | 6.299 | 0.085 | 6.325 | 0.072 | 6.326 | 0.071 |
| OCT61 | 6.209 | 0.075 | 6.174 | 0.087 | 6.209 | 0.076 | 6.209 | 0.074 |
| NOV61 | 6.063 | 0.079 | 6.043 | 0.089 | 6.064 | 0.079 | 6.064 | 0.077 |
| DEC61 | 6.168 | 0.082 | 6.174 | 0.086 | 6.168 | 0.082 | 6.169 | 0.080 |
Output 41.8.3 is based on Data2. It resembles Table 3 in Kohn and Ansley (1986). The columns S_SERIES and VS_SERIES in the OUTFOR=
data set contain the interpolated values of logair and their variances. The estimate column in Output 41.8.3 reports interpolated values (which are the same as S_SERIES), and the std column reports their standard errors (which are computed as square root of VS_SERIES) for January–November 1957. The actual logair values for these months, which are missing in Data2, are also provided for comparison. The numbers are very close to those in the article.
Output 41.8.3: Data Set 2: Interpolated Values and Standard Errors
Output 41.8.4 resembles Table 4 in Kohn and Ansley (1986). These numbers are based on Data3, and they also are very close to those in the article.
Output 41.8.4: Data Set 3: Interpolated Values and Standard Errors
Output 41.8.5 resembles Table 5 in Kohn and Ansley (1986). As before, the numbers are very close to those in the article.
Output 41.8.5: Data Set 4: Interpolated Values and Standard Errors
The similarity between the outputs in this example and the results shown in Kohn and Ansley (1986) demonstrate that PROC UCM can be effectively used for nonstationary ARIMA models with missing data.